4.4: The Electronic Basis of the Periodic Table
- Page ID
- 64725
The hydrogen-like orbitals for a many-electron atom are listed in order of increasing energy in Fig. 4-2. This energy level diagram differs from the corresponding diagram for the hydrogen atom, a one-electron system. In the many-electron atom all orbitals with the same value of the principal quantum number n do not have the same energy as they do in the case of hydrogen. For the many-electron atoms, the energy of an orbital depends on both n and l, the energy increasing as l increases even when n is constant. For example, from Fig. 4-2 it is evident that the 3d orbital possesses a higher energy than does the 3p orbital which in turn has a higher energy than does the 3p orbital. The reason for this difference between the one- and the many-electron case will be discussed below. The energy of the orbital is still independent of the magnetic quantum number m. Thus when l = 1, there are three p orbitals which are still degenerate (all possess the same energy) and this is indicated by the three open circles which are superimposed on each of the p levels. The open circles thus represent the number of available orbitals or the degeneracy of each orbital energy level.
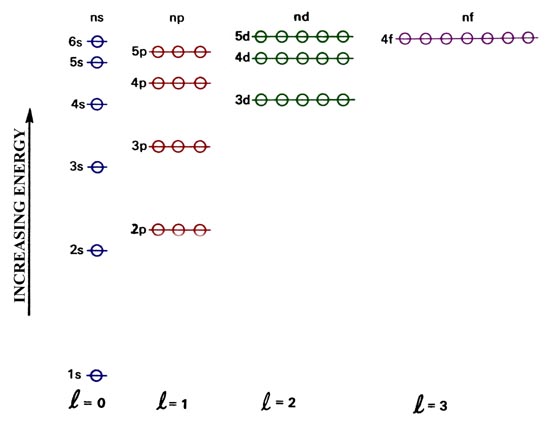
Fig. 4.2. An orbital energy level diagram for a many-electron atom.
With the aid of this energy level scheme and the Pauli principle we may proceed to build up the electronic structures of all the atoms. We do this by asssigning electrons one at a time to the vacant orbital which possesses the lowest energy. An orbital is "filled" when it contains two electrons with their spins paired.
Hydrogen. The nuclear charge is 1 and the single electron is placed in the 1s orbital. The electronic configuration is 1s1.
Helium. The nuclear charge is increased by one unit to 2 and the extra electron is again placed in the 1s orbital, with its spin opposed to that of the electron already present. The electronic configuration is 1s2.
Lithium. The nuclear charge is 3 and the third electron, because of the Pauli principle, must be placed in the 2s orbital as the 1s orbital is doubly occupied. The electronic configuration of lithium is therefore 1s22s1.
We can now answer the question as to why the 2s orbital is more stable than the 2p orbital, i.e., why Li is described as 1s22s1 and not as 1s22p1. The two inner electrons of lithium (those in the 1s orbital) partially shield the nuclear charge from the outer elctron. Recall that as n increases, the average distance between the electron and the nucleus increases. Thus most of tthe electron density of the electron with n = 2 will lie outside of the charge density of the two inner electrons which have n = 1. When the outer electron is at large distances from the nucleus and thus essentially outside of the inner shell of electron density it will experience a force from only one of the three positive charges on the lithium nucleus. However, as the outer electron does have a small but finite probability of being close to the nucleus, it will penetrate to some extent the tightly bound electron density of the two 1s electrons. In doing so it will "see" much more of the total nuclear charge and be more tightly bound. The closer the outer electron can get to the nucleus, that is, the more it can penetrate the density distribution of the inner shell electrons, the more tightly bound it will be.
An electron in an s orbital has a finite probability of being found right at the nucleus. An electron in a p orbital on the other hand has a node in its density distribution at the nucleus. Thus an s electron penetrates the inner shell density more effectively than does a p electron and is consequently more tightly bound to the atom. In a hydrogen atom, there are no inner electrons and both a 2s and 2p electron always experience the full nuclear charge and have the same energy. The crux of this penetration effect on the energy is that the inner shell electron density does possess a finite extension in space. Thus an outer electron can penetrate inner shell density and the screening effect is reduced. If the inner shell density was contracted right onto the nucleus, then no matter how close the outer electron came to the lithium nucleus, it would always experience only a charge of +1. This dependence of the orbital energies on their l value is aptly called the penetration effect.
The electron density of a d electron is concentrated even further away from the nucleus than is that of a p electron. Consequently, the orbital energy of a d electron is even less stable than that of a p electron. In some atoms the penetration of the inner shell density by a d electron is so slight that its energy is raised even over that of the s electron with the next highest n value. For example, a 3d electron possesses a higher energy than does a 4s electron in the atoms Sc to Zn with the exceptions of Cr and Cu. The penetration effect in these elements overrides the principal quantum number for d electrons in determining their relative energies.
Notice that the configuration 1s22s1 for lithium overcomes the difficulties of our earlier attempts to describe the electronic structure of this atom. The Pauli principle, of which we were ignorant in our previous attempt, forces the third electron to occupy the 2s orbital and forces in turn the beginning of a new quantum shell, that is, a new value of n. Thus lithium, like hydrogen, possesses one outer electron in an s orbital. Since it is only the outer electron density which in general is involved in a chemical change, lithium and hydrogen should have some chemical properties in common, as indeed they do. Hydrogen is the beginning of the first period (n = 1) and lithium marks the beginning of the second period (n = 2).
Beryllium. The nuclear charge is 4 and the electronic configuration is 1s22s2.
Boron. Z = 5 and the electron configuration is 1s22s22p1.
Carbon. Z = 6. The placing of the sixth electron of carbon requires some comment. It will obviously go into a 2p orbital. But in which of the three should it be placed? Should it be placed in the 2p orbital which already possesses one electron, or should it be placed in one of the vacant 2p orbitals? If it is placed in the occupied 2p orbital its spin must be paired with that of the electron already present and the result would be a nonmagnetic carbon atom. If, however, it is placed in one of the vacant 2p orbitals it may be assigned a spin parallel to the first electron. The question is decided on the grounds of which situation gives the lowest energy. As a result of the Pauli principle, two electrons with parallel spins (both up or both down) have only a very small probability of being close to one another. In fact the wave function which describes the two-electron case for parallel spins vanishes when both electrons approach one another. When the wave function vanishes, the corresponding probability distribution goes to zero. On the average, then, electrons with parallel spins tend to keep out of each other's way. Two electrons with paired spins, whether in the same or different orbitals are not prevented by the Pauli principle from being close to one another. The wave function for this situation is finite even when they are on top of one another! Obviously, two electrons with parallel spins will have a smaller value for the electrostatic energy of repulsion between them than will two electrons with paired spins. This is a general result which holds almost without exception in the orbital approximation. It is known as one of Hund's rules as he was the first to state it. Thus the most stable electronic configuration of the carbon atom is 1s22s22p2() where we have emphasized the fact that the two 2p electrons have parallel spins and hence must be in different 2p orbitals.
Nitrogen. Z = 7. Because of Hund's rule the electronic configuration is
i.e., one electron in each of the 2p orbitals. The configuration with the largest possible component of the spin magnetic moment will be the most stable.
Oxygen. Z = 8. One of the 2p electrons must now be paired with the added electron, but the other 2p electrons will be left unpaired.
(Only the number of unpaired electrons is indicated by the arrows.)
Fluorine. Z = 9. The configuration will be
Neon. Z = 10. The tenth electron will occupy the last remaining vacancy in the second quantum shell (the set of orbitals with n = 2).
Thus neon represents the end of the second period and all the electrons have paired spins.
When all the orbitals in a given shell are doubly occupied, the resulting configuration is called a "closed shell." Helium and neon are similar in that they both possess closed shell configurations. Because neither of these elements possesses a vacancy in its outer shell of orbitals both are endowed with similar chemical properties. When the orbitals belonging to a given l value contain either one electron each (are half-filled) or are completely filled, the resulting density distribution is spherical in shape. Thus the electron density distributions of nitrogen and neon, for example, will be spherical.
Reference to Fig. 4-2 indicates that the next element, sodium, will have its outer electron placed in the 3s orbital and it will be the first element in the third period. Since its outer electronic structure is similar to that of the preceding elements, lithium and hydrogen, it is placed beneath them in the periodic table. It is obvious that in passing from sodium to argon, all of the preceding outer electronic configurations found in the second period (n = 2) will be duplicated by the elements of the third period by filling the 3s and 3p orbitals. For example, the electronic structure of phosphorus (Z = 15) will be
and thus resemble nitrogen.
Argon. Z = 18. Argon will have filled 3s and 3p orbitals and will represent the end of a period. Argon, like helium and neon, possesses a closed shell structure and is placed beneath these two elements in the periodic table.
The Transition Elements
The beginning of the fourth period will be marked by the single and double occupation of the 4s orbital to give potassium and calcium respectively. However, reference to the orbital energy level diagram indicates that the 3dorbital is more stable than the 4p orbital. Since there are five d orbitals they may hold a total of ten electrons. Thus the ten elements beginning with scandium (Z = 21) will possess electronic structures which differ from any preceding them as they are the first elements to fill the d orbitals. A typical electronic configuration of one of these elements is that of manganese: [Ar]4s23d5. The symbol [Ar] is an abbreviated way of indicating that the inner shells of electrons on manganese possess the same orbital configuration as those of argon. In addition, the symbol 3d5 indicates that there are five electrons in the 3d orbitals, no distinction being made between the five different d orbitals. This series of elements in which the 3d orbitals are filled is called the first transition series. The element zinc with a configuration [Ar]4s23d10 marks the end of this series. The six elements from gallium to krypton mark the filling of the 4p orbitals and the closing, with krypton, of the fourth quantum shell and the fourth period of the table.
While the 3d orbitals are less stable than the 4s orbitals in the neutral atom (with the exceptions of Cr and Cu) and are filled only after the 4s orbitals are filled, the relative stability of the 4s and 3d orbitals is reversed in the ionic forms of the transition metals. For example, the configuration of the ion which results when the manganese atom loses two electrons is Mn+2 [Ar]3d5 and not [Ar]4s23d3. This is a general result. The d orbitals of quantum number n are filled only after the s orbital of quantum number (n + 1) is filled in the neutral atom, but the nd orbital is more stable than the (n + l)s orbital in the corresponding ion.
The fifth period begins with the filling of the 5s orbital, followed by the filling of the 4d orbitals, which generates the second transition series of elements. The period closes with the filling of the 5p orbitals and ends with xenon.
The lanthanide and actinide elements
The sixth period is started by the filling of the 6s orbital. The next element, lanthanum, has the electronic configuration [Xe]6s25d1. However, the next fourteen elements represent the beginning of another new series as the filling of the 4f orbitals is now energetically favoured over a continued increase in the population of the 5d orbitals. Note that the very small penetration effect possessed by the 4f orbitals (n = 4) delays their appearance until the sixth quantum shell has been partially filled. There are fourteen elements in this series, called the lanthanide series, since there are seven 4f orbitals (l = 3 and 2 ´ 3+1 = 7).
The third transition series follows the lanthanide elements as the occupation of the 5d orbitals is completed. This in turn is followed by the filling of the 6p orbitals. The final period begins with the filling of the 7s orbital and continues with the filling of the 5f orbitals. This second series of elements with electrons in f orbitals is called the actinide series.
The concept of atomic orbitals in conjunction with the Pauli principle has indeed predicted a periodicity in the electronic structures of the elements. The form of this periodicity duplicates exactly that found in the periodic table of the elements in which the periodicity is founded on the observed chemical and physical properties of the elements. Our next task will be to determine whether or not our proposed electronic structures will properly predict and explain the observed variations in the chemical and physical properties of the elements.

