4.3: The Magnetic Properties of the Electron
- Page ID
- 64678
So far, the only motion we have considered for the electron is a motion in three-dimensional space. Since this motion is ultimately described in terms of an orbital wave function, we term this the orbital motion of the electron. However, the electron may possess an internal motion of some kind, one which is independent of its motion through space. Since the electron bears a charge, such an internal motion, if it does exist, might be expected to generate a magnetic moment. We have previously pointed out that when an electron is in an atomic orbital for which l is not equal to zero, the resultant angular motion of the electron gives rise to a magnetic moment. We would anticipate then that an electron in an s orbital (l = 0) should not exhibit any magnetic effects as its angular momentum is zero. If an electron in these circumstances did exhibit a magnetic effect, it would indicate that another type of motion was possible, presumably an internal one. Whether or not an electron in an s orbital does possess a magnetic moment may be determined by means of an atomic beam experiment described below.
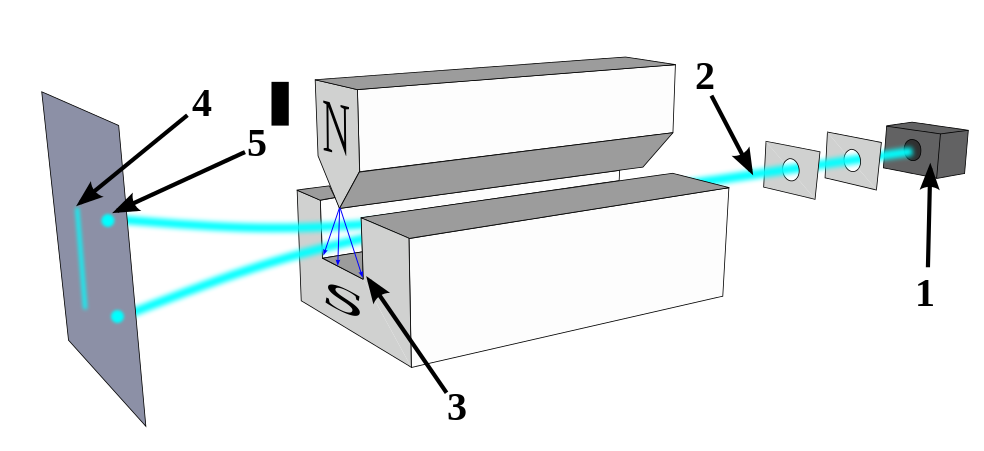
Ground-state Hydrogen atoms travel through an inhomogeneous magnetic field and are deflected up or down depending on their spin (which is based on the electron spin). (1) the hydrogen atom source, (2) collimated atomic beam, (3) inhomogeneous magnetic field, (4) the observed bifurcation of the beam (5) the predicted spread for a classical atom with no intrinsic electron spin. (CC SA-BY 4.0; Tatoute).
In the present experiment a beam of hydrogen atoms is passed through the apparatus. All of the hydrogen atoms in the beam will be in their ground state with l = 0 and hence they will not possess an orbital magnetic moment. However, when the magnetic field is applied, something does happen to the beam of atoms. It is split into two distinct beams, one of which is deflected to the N pole of the magnet and the other to the S pole. Thus even when atoms possess no magnetic moment because of the orbital motion of the electrons, they may still exhibit magnetic effects! As striking as the behaviour of the atoms as small magnets is the splitting of the beam into two distinct components. Let us consider first the origin of the magnetic effect, and second, the splitting of the beam into two distinct beams.
The observed magnetism of the hydrogen atoms must be due to some motion of the electrons. The nucleus of a hydrogen atom does possess a magnetic moment but its magnitude is too small, by a factor of roughly a thousand, to account for the deflections observed in this experiment. A magnetic moment will be observed only when the charged particle possesses angular momentum. Since the orbital angular momentum for an electron in the ground state of hydrogen is zero, we are forced to assume that the electron possesses some internal motion which has associated with it an angular momentum. A classical analogue of the internal angular momentum would be a spinning motion of the electron about its own axis. For this reason it is referred to as a spin angular momentum and the associated magnetic effect as a spin magnetic moment. These effects are separate from, and in addition to, the orbital angular momentum of the electron (classically, the rotation of the electron around the nucleus) and its associated magnetic effects.
We are familiar enough with the predictions of quantum mechanics to anticipate that the spin angular momentum and its component along some axis will be quantized. As in the case of orbital angular momentum, the effect of the quantization will be to limit the number of values which the component of the spin magnetic moment may have along any given axis. The magnitude of the spin angular momentum will determine the number of possible values its component may have along a given axis. Each of the possible values will in turn cause some fraction of the total spin magnetic moment to be aligned along the same axis. In the case of the electron's orbital motion, we found that as l and hence the orbital angular momentum was increased, the number of possible values for the component of the orbital magnetic moment along a given axis was increased, the number being equal to (2l + 1).
We can use a magnetic field to inquire into the nature of the spin angular momentum as well. In fact, we have already discussed the pertinent experiment. The beam of hydrogen atoms was split into just two components in the atomic beam experiment. This means that the component of the electron's spin magnetic moment (and spin angular momentum) along a given axis may have only one of two possible values; the component may be aligned with the field and hence be attracted, or it may be opposed to the field and be repelled. The electron's spin magnetic moment has been detected in many different kinds of experiments and the results are remarkable in that only two components of constant magnitude are ever observed. The electron is always either repelled by the field or attracted to it. This implies that the magnitude of the spin angular momentum for a single electron may have only one possible value. Since the number of possible values for the component of a given amount of angular momentum of any type in quantum mechanics is (2l + 1), l must equal ½ and only ½ for the spin angular momentum, and the values of m for the electron spin, which assume values from a maximum of l to a minimum of -l in steps of unity, must equal +½ and -½. In this respect the spin angular momentum of the electron is quite different from its orbital angular momentum, which may have many possible values, as the value of l for the orbital motion is restricted only in that it must equal zero or an integer.
It should be stressed that the splitting of the beam of hydrogen atoms into only two components is again evidence of quantization. If the atomic magnets (the hydrogen atoms) behaved according to classical mechanics, then the effect of the magnetic field would be simply to broaden the beam. The orientations of the atomic magnets would be random when they first entered the field of the magnet and classically the individual atomic magnets could be aligned at any and all angles with respect to the field, giving all possible components of the spin magnetic moment along the direction of the field. The inhomogeneous field would then exert a force proportional to the magnitude of the component, and the beam would broaden but not split.
Since the spin magnetic moment is an intrinsic property of the electron, even a beam of free electrons should be split into two components in a magnetic field. However, the charge possessed by the free electron also interacts with the magnetic field and the much smaller magnetic-magnetic interaction is masked by the usual deflection of a charge species in a magnetic field. By employing a neutral atom, the complications of the electronic charge may be avoided. The original experiment was performed on a beam of silver atoms by Stern and Gerlach in 1921. (We shall see shortly that the electrons in a silver atom do not possess any orbital angular momentum.)
Let us summarize what we have learned about this new property of the electron. Since an electron may exhibit a magnetic moment even when it does not possess orbital angular momentum, it must possess some internal motion. We call this motion the electron spin and treat it quantum mechanically as another kind of angular momentum. Experimentally, however, all we know is that the electron possesses an intrinsic magnetic moment. The remarkable feature of this intrinsic magnetic moment is that its magnitude and the number of components along a given axis are fixed. A given electron may exhibit only one of two possible components; it may be aligned with the field or against it. Experimentally, or theoretically, this is all we can know about the spin magnetic moment and the spin angular momentum. Hence only one quantum number is required to describe completely the spin properties of a single electron. We shall denote the value of this quantum number by or ¯, the upwards-pointing arrow signifying that the component of the magnetic moment is aligned with the field and the downwards-pointing arrow that this component is opposed to the field.
A total of four quantum numbers is required to specify completely the state of an electron when it is bound to an atom. The quantum numbers n, l and m determine its energy, orbital angular momentum and its component of orbital angular momentum. The fourth quantum number, the spin quantum number, summarizes all that can be known about the spin angular momentum of the electron. This final quantum number may have only one of two possible values corresponding to the magnetic moment component being (a) aligned with the field or (b) opposed to it.
The Pauli Exclusion Principle
The consequences of the spin quantum number, when applied to the problem of the electronic structure of atoms, are not immediately obvious. The small magnitude of the electron's magnetic moment does not directly affect the energy of the electron to any significant degree. To see just how the spin of the electron does influence the problem, let us reconsider our atomic orbital model in the light of this new degree of freedom for the electron. In particular let us reconsider those instances in which our model failed to account for the observations.
If a beam of helium atoms is passed through a magnetic field, no splitting and no deflection is observed. The helium atom, unlike the hydrogen atom is not magnetic. We could account for the absence of a magnetic moment for helium if we assumed that of the two electrons in the helium 1s orbital, one had its magnetic moment component up (↑) and the other down (¯). The two components would then cancel and there would be no resultant magnetic effect. Our complete description of the electronic configuration of the helium atom would be 1s2(¯), i.e., both electrons have n = 1, l = 0, m = 0 and one has a spin (↑) and the other a spin (↓).
You may wonder why the states of helium corresponding to the configurations 1s2(↑↑) or 1s2(↓↓) are not observed. These states should exhibit twice the magnetism possessed by a hydrogen atom. They are, however not found to occur. What about the excited states of the helium atom? An excited state results when one electron is raised in energy to an orbital with a higher n value. The electrons are thus in different orbitals. The spin assignments for an excited configuration can be made in more than one way and are such as to predict the occurrence of both magnetic and non-magnetic helium. For example, the configuration 1s12s1 could be 1s1(↑)2s1(↓) and be nonmagnetic or it could equally well be 1s1(↓)2s1(↓) or 1s1(↑)2s1(↑) and be magnetic.
Care must be exercised in the use of the abbreviated notation 1s1(↑)2s1(↓) to indicate the configuration and spin of a many-electron atom. In the present example, all we mean to imply is that the total component of the spin is zero. We do not imply that the electron in the 1s orbital necessarily has a spin "up" and that in the 2s orbital a spin "down." The situation could equally well be described by the notation 1s1(↓)2s1(↑). There is no experimental method by which we can distinguish between electrons in an atom, or, for that matter, determine any property of an individual electron in a many-electron system. Only the total magnetic moment, or total angular momentum, may be determined experimentally.
Both the magnetic and non-magnetic forms are indeed found to occur for helium in an excited state. There are in fact two kinds of excited helium atoms, those which are non-magnetic and those which are magnetic. If the two forms of helium possess different energies even though they have the same orbital configuration (we shall see why this should be so later) then we have an explanation for the previously noted discrepancy that helium exhibits twice the number of line spectra as does hydrogen. For every set of lines in the spectrum which arises from the transition of the electron from the configurations 1s1(↑)np1(¯) to the configuration 1s1(↑)2s1(¯) for example, there will be another set of lines due to transitions from 1s1(↑)np1(¯) to 1s1(↑)2s1(¯).
The study of the magnetic properties of the ground and excited states of helium is sufficient to point out a general principle. For the ground state of helium, in which both electrons are in the same atomic orbital, only the non-magnetic form exists. This would imply that when two electrons are in the same atomic orbital their spins must be paired, that is, one up (↑) and one down (¯). This is an experimental fact because helium is never found to be magnetic when it is in its electronic ground state. When the electrons are in different orbitals, then it is again an experimental fact that their spins may now be either paired (¯↑) or unpaired, e.g., (↑). Thus when two electrons are in the same orbital (i.e., they possess the same n, l and m values) their spins must be paired. When they are in different orbitals (one or more of their n, l and m values are different) then their spins may be paired or unpaired. We could generalize these observations by stating that "no two electrons in the same atom may have all four quantum numbers the same." Stated in this way we see immediately that any given orbital may hold no more than two electrons. Since two electrons in the same orbital have the same values of n, l and m, they can differ only through their spin quantum number. However, the spin quantum number may have only one of two possible values, and these possibilities are given by (n, l, m, ↑ ) or (n, l, m, ¯).
We have indeed found the principle we were seeking, one which limits the occupation of an atomic orbital. This principle is known as the Pauli exclusion principle. One form of it, suitable for use within the framework of the orbital approximation, is the statement given in quotation marks above. The Pauli principle cannot be derived from, nor is it predicted by, quantum mechanics. It is a law of nature which must be taken into account along with quantum mechanics if the properties of matter are to be correctly described. The concept of atomic orbitals, as derived from quantum mechanics, together with the Pauli exclusion principle which limits the occupation of a given orbital, provides an understanding of the electronic structure of many-electron atoms. We shall demonstrate this by "predicting" the existence of the periodic table.

