7.3: Molecular Dynamics Simulations
- Page ID
- 17634
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)One thing that the MC process does not address directly is the time evolution of the system. That is, the steps one examines in the MC algorithm are not straightforward to associate with a time-duration, so it is not designed to compute the rates at which events take place. If one is interested in simulating such dynamical processes, even when the N-molecule system is at or near equilibrium, it is more appropriate to carry out a classical molecular dynamics (MD) simulation. In such an MD calculation, one has to assign initial values for each of the internal and external coordinates of each of the \(N\) molecules and an initial value of the kinetic energy or momentum for each coordinate, after which a time-propagation algorithm generates values for the coordinates and momenta at later times. For example, the initial coordinates could be chosen close to those of a local minimum on the energy surface and the initial momenta associated with each coordinate could be assigned values chosen from a Maxwell-Boltzmann distribution characteristic of a specified temperature T. In such cases, it is common to then allow the MD trajectory to be propagated for a length of time \(\Delta t\) long enough to allow further equilibration of the energy among all degrees of freedom before extracting any numerical data to use in evaluating average values or creating inter-particle distance histograms, for example.
One usually does not choose just one set of such initial coordinates and momenta to generate a single trajectory. Rather, one creates an ensemble of initial coordinates and momenta designed to represent the experimental conditions the MD calculation is to simulate. The time evolution of the system for each set of initial conditions is then followed using MD and various outcomes (e.g., reactive events, barrier crossings, folding or unfolding events, chemisorption ocurrences, etc.) are monitored throughout each MD simulation. An average over the ensemble of trajectories is then used in computing averages and creating histograms for the MD simulation. It is the purpose of this Section to describe how MD is used to follow the time evolution for such simulations.
Trajectory Propagation
With each coordinate having its initial velocity \(\left(\dfrac{dq}{\delta t}\right)_0\) and its initial value \(q_0\) specified, one then uses Newton’s equations written for a time step of duration \(\delta t\) to propagate \(q\) and \(dq/dt\) forward in time according, for example , to the following first-order propagation formula:
\[q(t+\delta t) = q_0 + \left(\dfrac{dq}{\delta t}\right)_0 dt\]
\[\dfrac{dq}{dt} (t+\delta t) = \left(\dfrac{dq}{dt}\right)_0 - \delta t \left[\left( \dfrac{∂V}{∂q} \right)_0\dfrac{1}{m_q}\right].\]
Here m_q is the mass factor connecting the velocity \(dq/dt\) and the momentum pq conjugate to the coordinate q:
\[p_q = m_q \dfrac{dq}{dt},\]
and \(-(∂V/∂q)_0\) is the force along the coordinate \(q\) at the earlier geometry \(q_0\). In most modern MD simulations, more sophisticated numerical methods can be used to propagate the coordinates and momenta. For example, the widely used Verlet algorithm is derived as follows.
- One expands the value of the coordinate \(q\) at the \(n+1^{\rm st}\) and \(n-1^{\rm st}\) time steps in Taylor series in terms of values at the \(n\)st time step \[q_{n+1}=q_n+\left(\dfrac{dq}{dt}\right)_n\delta t +\dfrac{-\left( \dfrac{∂V}{∂q} \right)_n}{2m_q}\delta t^2-O(\delta t^3) \]
\[q_{n-1}=q_n-\left(\dfrac{dq}{dt}\right)_n\delta t +\dfrac{\left( \dfrac{∂V}{∂q} \right)_n}{2m_q}\delta t^2+O(\delta t^3)\] - One adds these two expansions to obtain
\[q_{n+1}=2 q_n-q_{n-1}+\dfrac{-\left( \dfrac{∂V}{∂q} \right)_n}{2m_q}\delta t^2-O(\delta t^4)\]
which allows one to compute \(q_{n+1}\) in terms of \(q_{n}\) and \(q_{n-1}\) and the force at the \(n^{\rm th}\) step, while not requiring knowledge of velocities. - If the two Taylor expansions are subtracted, one obtains \[\left(\dfrac{dq}{dt}\right)_{n+1}-\dfrac{q_{n+1}-q_{n-1}}{2\delta t}+O(\delta t^2)\] as the expression for the velocity at the \(n+1^{\rm st}\) time step in terms of the coordinates at the \(n+1^{\rm st}\) and \(n-1^{\rm st}\) steps.
There are many other such propagation schemes that can be used in MD; each has strengths and weaknesses. In the present Section, I will focus on describing the basic idea of how MD simulations are performed while leaving treatment of details about propagation schemes to more advanced sources such as Computer Simulations of Liquids, M. P. Allen and D. J. Tildesley, Oxford U. Press, New York (1997).
The forces \(-(∂V/∂q)\) appearing in the MD propagation algorithms can be obtained as gradients of a Born-Oppenheimer electronic energy surface if this is computationally feasible. Following this path involves performing what is called direct-dynamics MD. Alternatively, the forces can be computed from derivatives of an empirical force field. In the latter case, the system's potential energy \(V\) is expressed in terms of analytical functions of
- intramolecular bond lengths, bond angles, and torsional angles, as well as
- intermolecular distances and orientations.
The parameters appearing in such force fields have usually been determined from electronic structure calculations on molecular fragments, spectroscopic determination of vibrational force constants, and experimental measurements of intermolecular forces.
Force Fields
Let’s interrupt our discussion of MD propagation of coordinates and velocities to examine the ingredients that usually appear in the force fields mentioned above. In Figure 7.3 c, we see a molecule in which various intramolecular and intermolecular interactions are introduced.

The total potential of a system containing one or more such molecules in the presence of a solvent (e.g., water) it typically written as a sum of intramolecular potentials (one for each molecule in the system) and itermolecular potentials. The former are usually decomposed into a sum of covalent interactions describing how the energy varies with bond stretching, bond bending, and dihedral angle distortion as depicted in Figure 7.3 d.
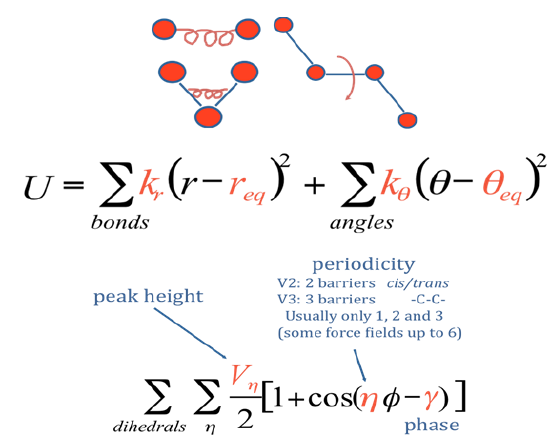
and non-covalent interactions describing electrostatic and van der Waals interactions among the atoms in the molecule a
\[V_{\rm noncovalent}=\sum_{i<j}^{\rm atoms} \left[\dfrac{A_{i,j}}{r_{i,j}^{12}}-\dfrac{B_{i,j}}{r_{i,j}^{6}}+\dfrac{q_iq_j}{\varepsilon r_{i,j}}\right].\]
These functional forms would be used to describe how the energy \(V(q)\) changes with the bond lengths (\(r\)) and angles (\(\theta,\phi\)) within, for example, each of the molecules shown in Figure 7. 3 c (let’s call them solute molecules) as well as for any water molecules that may be present (if these molecules are explicitly included in the MD simulation).
The interactions among the solute and solvent moleulues are also often expressed in a form involving electrostatic and van der Waals interations between pairs of atoms- one on one molecule (solute or solvent) and the other on another molecule (solute or solvent)
\[V_{\rm intermolecular} = \sum_{i<j}^{\rm atoms} \left[\dfrac{A_{i,j}}{r_{i,j}^{12}}-\dfrac{B_{i,j}}{r_{i,j}^{6}}+\dfrac{q_iq_j}{\varepsilon r_{i,j}}\right].\]
The Cartesian forces on any atom within a solute or solvent molecule are then computed for use in the MD simulation by using the chain rule to relate derivatives with respect to Cartesian coordinates to derivatives of the above intramolecular and intermolecular potentials with respect to the interatomic distances and the angles appearing in them.
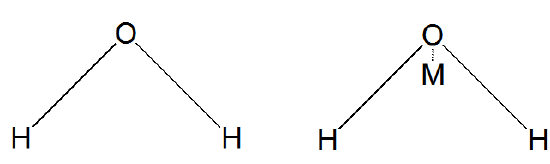
Because water is such a ubiquitous component in condensed-phase chemistry, much effort has been devoted to generating highly accurate intermolecular potentials to describe the interactions among water molecules. In the popular TIP3P and TIP4P models, the water-water interaction is given by
\[V = \dfrac{A}{r_{OO}^{12}}-\dfrac{B}{r_{OO}^{6}}+\sum_{i,j}\dfrac{kq_iq_j}{r_{i,j}}.\]
where rOO is the distance between the oxygen atoms of the two water molecules in Å, and indices \(i\) and \(j\) run over 3 or 4 sites, respectively, for TIP3P or TIP4P, with \(i\) labeling sites on one water molecule and \(j\) labeling sites on the second water molecule. The parameter \(k\) is 332.1 Å kcal mol-1. A and B are conventional Lennard-Jones parameters for oxygen atoms and qi is the magnitude of the partial charge on the ith site. In Figure 7.3 d, we show how the 3 or 4 sites are defined for these two models.
Typical values for the parameters are given in the table below.
|
rOH(Å) |
HOH angle degrees |
rOM(Å) |
A (Å12 kcal/mol) |
B (Å6 kcal/mol) |
qOor qM |
qH |
|
|---|---|---|---|---|---|---|---|
|
TIP3P |
0.9572 |
104.52 |
582 x103 |
595 |
-0.834 |
0.417 |
|
|
TIP4P |
0.9672 |
104.52 |
0.15 |
600 x103 |
610 |
-1.04 |
0.52 |
In the TIP3P model, the three sites reside on the oxygen and two hydrogen centers. For TIP4P, the fourth site is called the M-site and it resides off the oxygen center a distance of 0.15 along the bisector of the two O-H bonds as shown in Figure 7.3 d. In using either the TIP3P or TIP4P model, the intramolecular bond lengths and angles are often constrained to remain fixed; when doing so, one is said to be using a rigid water model.
There are variants to these two 3-site and 4-site models that, for example, include van der Waals interactions between \(H\) atoms on different water molecules, and there are models including more than 4 sites, and models that allow for the polarization of each water molecule induced by the dipole fields (as represented by the partial charges) of the other water molecules and of solute molecules. The more detail and complexity one introduces, the more computational effort is needed to perform MD simulations. In particular, water molecules that allow for polarization are considerably more computationally demanding because they often involve solving self-consistently for the polarization of each molecule by the charge and dipole potentials of all the other molecules, with each dipole potential including both the permanent and induced dipoles of that molecule. Professor John Wampler has created a web page in which the details about molecular mechanics force fields introduced above are summarized. This web page provides links to numerous software packages that use these kinds of force fields to carry out MD simulations. These links also offer more detailed information about the performance of various force fields as well as giving values for the parameters used in those force fields.
The parameter values are usually obtained by
- fitting the intramolecular or intermolecular functional form (e.g., as shown above) to energies obtained in electronic structure calculations at a large number of geometries, or
- adjusting them to cause MD or MC simulations employing the force field to reproduce certain thermodynamic properties (e.g., radial distribution functions, solvation energies, vaporization energies, diffusion constants), or some combination of both. It is important to observe that the kind of force fields discussed above have limitations beyond issues of accuracy. In particular, they are not designed to allow for bond breaking and bond forming, and they represent the Born-Oppenheimer energy of one (most often the ground) electronic state. There are force fields explicitly designed to include chemical bonding changes, but most MD packages do not include them. When one is interested in treating a problem that involves transitions from one electronic state to another (e.g., in spectroscopy or when the system undergoes a surface hop near a conical intersection), it is most common to use a combined QM-MM approach like we talked about in Section 6.1.3 of Chapter 6. A QM treatment of the portion of the system that undergoes the electronic transition is combined with a force-field (MM) treatment of the rest of the system to carry out the MD simulation. Let’s now return to the issue of propagating trajectories given a force field and a set of initial conditions appropriate to describing the system to be simulated.
By applying one of the time-propagation algorithms to all of the coordinates and momenta of the \(N\) molecules at time t, one generates a set of new coordinates \(q(t+\delta t)\) and new velocities \(dq/dt(t+\delta t)\) appropriate to the system at time \(t+dt\). Using these new coordinates and momenta as \(q_0\) and \((dq/\delta t)_0\) and evaluating the forces \(–(∂V/∂q)_0\) at these new coordinates, one can again use the propagation equations to generate another finite-time-step set of new coordinates and velocities. Through the sequential application of this process, one generates a sequence of coordinates and velocities that simulate the system’s behavior. By following these coordinates and momenta, one can interrogate any dynamical properties that one is interested in. For example, one could monitor oxygen-oxygen distances throughout an MD simulation of liquid water with initial conditions chosen to represent water at a given temperature (T would determine the initial momenta) to generate a histogram of O-O distances. This would allow one to construct the kind of radial distribution function shown in Figure 7. 3 using MD simulation rather than MC. The radial distribution function obtained in such an MD simulation should be identical to that obtained from MC because statistical mechanics assumes the ensemble average (MC) is equal to the long-time average (MD) of any property for a system at equilibrium. Of course, one could also monitor quantities that depend on time, such as how often two oxygen atoms come within a certain distance, throughout the MD simulation. This kind of interrogation could not be achieved using MC because there is no sense of time in MC simulations.
In Chapter 8, I again discuss using classical molecular dynamics to follow the time evolution of a chemical system. However, there is a fundamental difference between the kind of simulations described above and the case I treat in Chapter 8. In the former, one allows the N-molecule system to reach equilibrium (i.e., either by carefully choosing initial coordinates and momenta or by waiting until the dynamics has randomized the energy) before monitoring the subsequent time evolution. In the problem discussed in Chapter 8, we use MD to follow the time progress of a system representing a single bimolecular collision in two crossed beams of molecules. Each such beam contains molecules whose initial translational velocities are narrowly defined rather than Maxwell-Boltzmann distributed. In this case, we do not allow the system to equilibrate because we are not trying to model an equilibrium system. Instead, we select an ensemble of initial conditions that represent the molecules in the two beams and we then follow the Newton dynamics to monitor the outcome (e.g., reaction or non-reactive collision).
Unlike the MC method, which is very amenable to parallel computation, MD simulations are more difficult to carry out in a parallel manner. One can certainly execute many different classical trajectories on many different computer nodes; however, to distribute one trajectory over many nodes is difficult. The primary difficulty is that, for each time step, all \(N\) of the molecules undergo moves to new coordinates and momenta. To compute the forces on all \(N\) molecules requires of the order of \(N^2\) calculations (e.g., when pairwise additive potentials are used). In contrast, each MC step requires that one evaluate the potential energy change accompanying the displacement of only one molecule. This uses only of the order of \(N\) computational steps (again, for pair wise additive potentials).
Another factor that complicates MD simulations has to do with the wide range of times scales that may be involved. For example, for one to use a time step dt short enough to follow high-frequency motions (e.g., O-H stretching) in a simulation of an ion or polymer in water solvent, dt must be of the order of 10-15 s. To then simulate the diffusion of an ion or the folding of a polymer in the liquid state, which might require 10-4 s or longer, one would have to carry out 1011 MD steps. This likely would render the simulation not feasible. In the table below we illustrate the wide range of time scales that characterize various events that one might want to simulate using some form of MD, and we give a sense of what is practical using MD simulations in the year 2010.
|
10-15 -10-14 s |
10-12 s |
10-9 s |
10-6 s |
10-3 s |
110 s |
|---|---|---|---|---|---|
|
C-H, N-H, O-H bond vibration |
Rotation of small molecule |
Routinely accessible time duration for atomistic MD simulation |
Time duration for heroic atomistic MD simulation |
Time duration achievable using coarse-graining techniquesa |
Time needed for protein folding |
a. These techniques are discussed in Section 7.3.3.
Because one can not afford to carry out simulations covering 10-3 -100 s using time steps needed to follow bond vibrations 10-15 s, it is necessary to devise strategies to focus on motions whose time frame is of primary interest while ignoring or approximating faster motions. For example, when carrying out long-time MD simulations, one can ignore the high-frequency intramolecular motions by simply not including these coordinates and momenta in the Netwonian dynamics (e.g., as one does when using a rigid-water model discussed earlier). In other words, one simply freezes certain bond lengths and angles. Of course, this is an approximation whose consequences must be tested and justified, and would certainly not be a wise step to take if those coordinates played a key role in the dynamical process being simulated. Another approach, called coarse graining involves replacing the fully atomistic description of selected components of the system by a much-simplified description involving significantly fewer spatial coordinates and momenta.
Coarse Graining
The goal of coarse graining is to bring the computational cost of a simulation into the realm of reality. This is done by replacing the fully atomistic description of the system, in which coordinates sufficient to specify the positions (and, in MD, the velocities) of every atom, by a description in terms of fewer functional groups often referred to as “beads”. The TIP4P and TIP3P models for the water-water interaction potential discussed above are not coarse-grained models because they contain as many (or more) centers as atoms. An example of a coarse-grained model for the water-water interaction is provided by the Stillinger-Weber model (that was originally introduced to treat tetrahedral Si) of water introduced in V. Molinero and E. B. Moore, J. Phys. Chem. B 2009, 113, 4008–4016. Here, each water molecule is described only by the location of its oxygen nucleus (labeled ri for the ith water molecule), and the interaction potential is given as a sum of two-body and three-body terms
\[V=\sum_{i<j=1}^N A\varepsilon\left[B\left(\dfrac{\sigma}{r_{i,j}}\right)^p-\left(\dfrac{\sigma}{r_{i,j}}\right)^q\right]\exp\left(\dfrac{\sigma}{r_{i,j}-a\sigma}\right)\\+\sum_{i<j<k=1}^N \lambda \varepsilon[\cos\theta_{i,j,k}-\cos\theta_0]^2\exp\left(\dfrac{\gamma\sigma}{r_{i,j}-a\sigma}\right)\exp\left(\dfrac{\gamma\sigma}{r_{i,k}-a\sigma}\right)\]
where \(r_{i,j}\) is the distance between the ith and jth oxygen atom, \(\theta_0 =\) 109.47 deg, and \(q_{i,j,k}\) is the angle between the ith (at the center), jth, and kth oxygen atom. The parameters \(A\), \(B\), \(\varepsilon\), \(\sigma\), and \(a\) are used to characterize various characteristics of the potential; different values are needed to describe the behavior of Si, Ge, diamond, or water even though they all can adopt tetrahedral coordination. The form of the three-body part of this potential is designed to guide the orientations among oxygen atoms to adopt tetrahedral character.
Although the above potential seems more complicated than, for example, the form used in the TIP3P or TIP4P potential, it has three important advantages when it comes to carrying out MD simulations:
- Because the SW potential contains no terms varying with distance as \(r^{-1}\) (i.e., no Coulomb interactions among partial charges), it is of qualitatively shorter range than the other two potentials. This allows spatial cut-offs to be used (i.e., to ignore interactions beyond much shorter distances) efficiently.
- 2. For a system containing \(N\) water molecules, the TIP3P or TIP4P models require one to evaluate functions of the distances between \((3N)^2/2\) or \((4N)^2/2\) centers, whereas the SW’s two-body component involves only \(N^2/2\) interactions and the three-body component need only be evaluated for molecules \(j\) and \(k\) that are nearby molecule \(i\).
- 3. If, for the atomistic models, one wishes to treat the O-H stretching and H-O-H bending motions, MD time steps of ca. 10-15 s must be employed. For the SW model, the fastest motions involve relative movements of the oxygen centers, which occur on time scales ca. 10 times longer. This means that one can use longer MD steps.
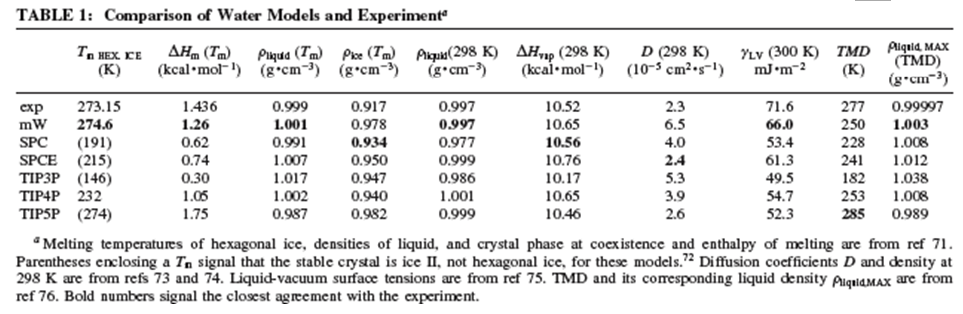
The net result is that this coarse-grained model of the water-water interaction allows MD simulations to be carried out for qualitatively longer time durations. Of course, this is only an advantage if the simulations provide accurate results. In the Table shown below (taken from the above reference), we see MD simulation results (as well as experimental results) obtained with the above (mW) model, with various TIPnP models, and with two other popular water-water potentials (SPC and SPCE) from which it is clear that the coarse-grained mW model is capable of yielding reliable results on a range of thermodynamic properties.
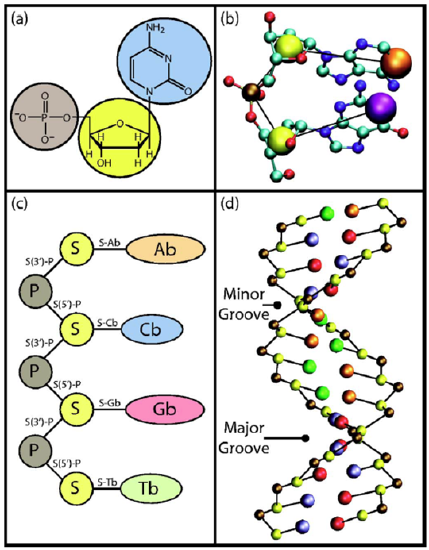
In the Table shown below, the reference cited above specifies the locations and masses of the phosphate, sugar, and base beads in the B form of the DNA helix. The masses need to be chosen so that the coarse-grained dynamical motions of these units replicate within reasonable tolerances the center of mass motions of the phosphate, sugar, and base moieties when atomistic MD simulations are carried out on smaller test systems containing these nucleotide units.
The potential \(V\) used to carry out the coarse-grained MD simulations is given by the equations shown below taken from the above reference. In addition to the usual bond stretching, bending and dihedral terms (n.b., now the bonds relate to linkages between beads rather than between atoms) that are similar to what we saw earlier in our discussion of force fields, there are additional terms.
- \(V_{\rm stack}\) describes the interactions among p-stacked base pairs,
- \(V_{\rm bp}\) describes the hydrogen bonding interactions between bases, and
- \(V_{\rm ex}\) describes excluded-volume effects.
\[V_{\rm total}=V_{\rm bond}+V_{\rm angle}+V_{\rm dihedral}+V_{\rm stack}+V_{\rm bp}+V_{\rm ex}+V_{\rm qq},\]
where
\[V_{\rm bond}=\sum_i^{N_{\rm bond}}[k_1(d_i-d_{0_i})^2+k_2(d_i-d_{0_i})^4],\]
\[V_{\rm angle}=\sum_i^{N_{\rm angle}}\dfrac{k_\theta}{2}(\theta_i-\theta_{0_i})^2,\]
\[V_{\rm dihedral}=\sum_i^{N_{\rm dihedral}}k_\phi [1-\cos(\phi_i-\phi_{0_i})],\]
\[V_{\rm stack}=\sum_{i<j}^{N_{\rm st}} 4\varepsilon\left[\left(\dfrac{\sigma_{ij}}{r_{ij}}\right)^{12}-\left(\dfrac{\sigma_{ij}}{r_{ij}}\right)^6\right],\]
\[V_{\rm bp}=\sum_{\rm base pairs}^{N_{\rm bp}} 4\varepsilon_{\text{bp}{}_i}\left[5\left(\dfrac{\sigma_{\text{bp}{}_i}}{r_{ij}}\right)^{12}-6\left(\dfrac{\sigma_{\text{bp}{}_i}}{r_{ij}}\right)^{10}\right],\]
\[V_{\rm ex}=\sum_{i<j}^{N_{\rm ex}} \left\{\begin{array}{cc}
4\varepsilon\left[\left(\dfrac{\sigma_{ij}}{r_{ij}}\right)^{12}-\left(\dfrac{\sigma_{ij}}{r_{ij}}\right)^6\right]+\varepsilon & \text{if } r_{ij}<d_{\rm cut}\\
0 & \text{if } r_{ij}\ge d_{\rm cut}
\end{array}\right.,\]
\[V_{\rm qq}=\sum_{i<j}^N\dfrac{q_iq_j}{4\pi\varepsilon_0 \varepsilon_k r_{ij}}e^{-r'_{ij}\kappa_D}.\]
4. \(V_{\rm qq}\) is the screened Coulombic interactions among phosphate units, with its exponential decay constant \(\kappa_D\) given in terms of a so-called Debye screening length as detailed in the above reference.
The values of the parameters used in this force field potential given in the above reference are reproduced in the two Tables shown below.
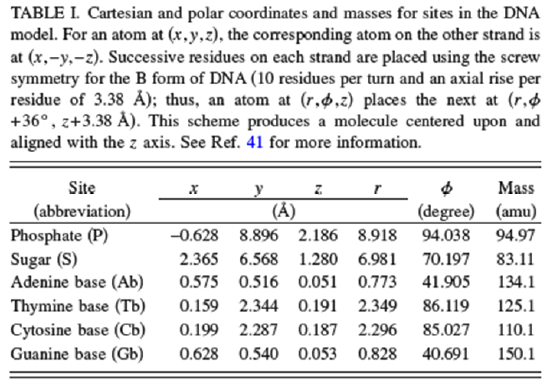
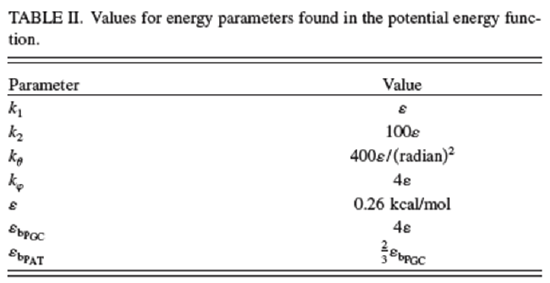
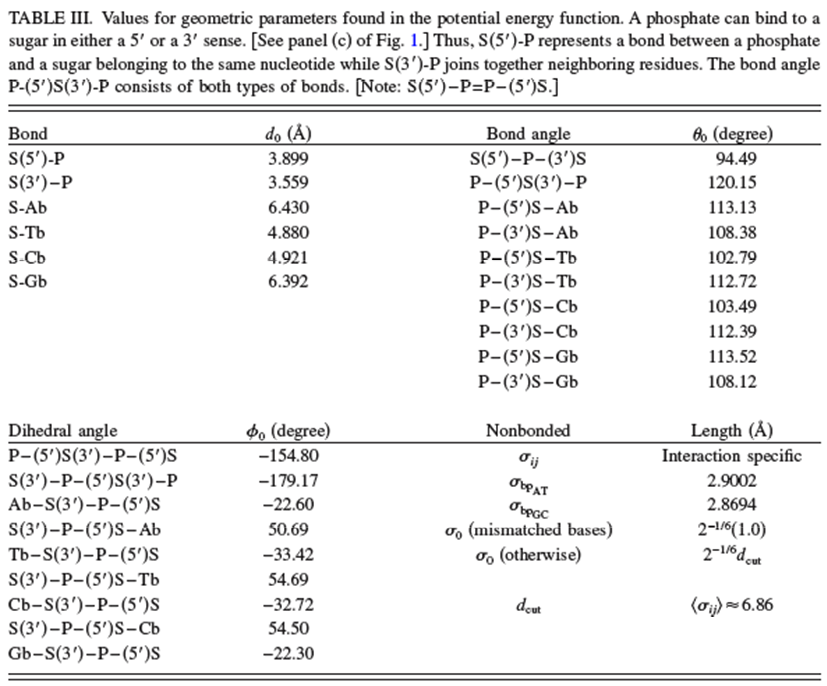
Although there are numerous parameters in this potential, the key to the success of this coarse graining is that there are only six kinds of sites whose positions and velocities must be propagated in the MD simulation- phosphate sites, sugar sites, and four kinds of base sites. This is far fewer coordinates that would arise in a fully atomistic MD simulation. I will refer the reader to the reference cited above for details about how successful coarse graining was in this case, but I will not go further into it at this time. I think the two examples we discussed in this Section suffice for introducing the subject of coarse graining to the readers of this text.In summary for this Section, MD classical simulations are not difficult to implement if one has available a proper representation of the intramolecular and intermolecular potential energy V. Such calculations are routinely carried out on large bio-molecules or condensed-media systems containing thousands to millions of atomic centers. There are, however, difficulties primarily connected to the time scales over which molecular motions and over which the process being simulated change that limit the success of this method and which often require one to employ reduced representations of the system such as in coarse graining. In contrast, quantum MD simulations such as we describe in the following Section are considerably more difficult to carry out.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


