7.2: Monte Carlo Evaluation of Properties
- Page ID
- 11596
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A tool that has proven extremely powerful in statistical mechanics since computers became fast enough to permit simulations of complex systems is the Monte Carlo (MC) method. This method allows one to evaluate the integrations appearing in the classical partition function described above by generating a sequence of configurations (i.e., locations of all of the molecules in the system as well as of all the internal coordinates of these molecules) and assigning a weighting factor to these configurations. By introducing an especially efficient way to generate configurations that have high weighting, the MC method allows us to simulate extremely complex systems that may contain millions of molecules.
To appreciate why it is useful to have a tool such as MC, let’s consider how one might write a computer program to evaluate the classical partition function
\[Q = \frac{h^{-NM}}{N!} \int \exp (- H(q, p)/kT)\,dq \,dp\]
For a system consisting of \(N\) Ar atoms in a box of volume \(V\) at temperature T. The classical Hamiltonian \(H(q,p)\) consists of a sum of kinetic and inter-atomic potential energies
\[H(p,q)=\sum_{i=1}^N\frac{p_i^2}{2m}+V(q)\]
The integration over the \(3N\) momentum variables can be carried out analytically and allows \(Q\) to be written as
\[Q=\frac{1}{N!}\left(\frac{2\pi mkT}{\hbar^2}\right)^{3N/2}\int \exp\left[-\frac{V(q_1,q_2,\cdots,q_{3N})}{kT}\right]dq_1dq_2\cdots dq_{3N-1}\]
The contribution to \(Q\) provided by the integral over the coordinates is often called the configurational partition function
\[Q_{\rm config}=\int \exp\left[-\frac{V(q_1,q_2,\cdots,q_{3N})}{kT}\right]dq_1dq_2\cdots dq_{3N-1}\]
If the density of the \(N\) Ar atoms is high, as in a liquid or solid state, the potential \(V\) will depend on the \(3N\) coordinates of the Ar atoms in a manner that would not allow substantial further approximations to be made. One would thus be faced with evaluating an integral over \(3N\) spatial coordinates of a function that depends on all of these coordinates. If one were to discretize each of the \(3N\) coordinate axes using say \(K\) points along each axis, the numerical evaluation of this integral as a sum over the \(3N\) coordinates would require computational effort scaling as K3N. Even for 10 Ar atoms with each axis having \(K\) = 10 points, this is of the order of 1030 computer operations. Clearly, such a straightforward evaluation of this classical integral would be foolish to undertake.
The MC procedure allows one to evaluate such high-dimensional integrals by
- not dividing each of the \(3N\) axes into \(K\) discrete points, but rather
- selecting values of \(q_1, q_2, \cdots q_{3N}\) for which the integrand \(\exp(-V/kT)\) is non-negligible, while also
- avoiding values of \(q_1, q_2, \cdots q_{3N}\) for which the integrand \(\exp(-V/kT)\) is small enough to neglect.
By then summing over only values of \(q_1, q_2, \cdots q_{3N}\) that meet these criteria, the MC process can estimate the integral. Of course, the magic lies in how one designs a rigorous and computationally efficient algorithm for selecting those \(q_1, q_2, \cdots q_{3N}\) that meet the criteria.
To illustrate how the MC process works, let us consider carrying out a MC simulation representative of liquid water at some density r and temperature T. One begins by placing \(N\) water molecules in a box of volume \(V\) chosen such that \(N/V\) reproduces the specified density. To effect the MC process, we must assume that the total (intramolecular and intermolecular) potential energy \(V\) of these \(N\) water molecules can be computed for any arrangement of the \(N\) molecules within the box and for any values of the internal bond lengths and angles of the water molecules. Notice that, as we showed above when considering the Ar example, \(V\) does not include the kinetic energy of the molecules; it is only the potential energy. Often, this energy \(V\) is expressed as a sum of intra-molecular bond-stretching and bending contributions, one for each molecule, plus a pair-wise additive intermolecular potential:
\[V = \sum_J V_{\rm (internal)}{}_J + \sum_{J,K} V_{\rm (intermolecular)}{}_{J,K},\]
although the MC process does not require that one employ such a decomposition; the energy \(V\) could be computed in other ways, if appropriate. For example, \(V\) might be evaluated as the Born-Oppenheimer energy if an ab initio electronic structure calculation on the full \(N\)-molecule system were feasible. The MC process does not depend on how \(V\) is computed, but, most commonly, it is evaluated as shown above.
Metropolis Monte Carlo
In each step of the MC process, this potential energy \(V\) is evaluated for the current positions of the \(N\) water molecules. In its most common and straightforward implementation known as the Metropolis Monte-Carlo process, a single water molecule is then chosen at random and one of its internal (bond lengths or angle) or external (position or orientation) coordinates is selected at random. This one coordinate (q) is then altered by a small amount (\(q \rightarrow q+\delta q;ta{q}\)) and the potential energy \(V\) is evaluated at the new configuration (\(q+\delta q\)). The amount \(\delta{q}\) by which coordinates are varied is usually chosen to make the fraction of MC steps that are accepted (by following the procedure detailed below) approximately 50%. This has been shown to optimize the performance of the MC algorithm.
In implementing the MC process, it is usually important to consider carefully how one defines the coordinates \(q\) that will be used to generate the MC steps. For example, in the case of \(N\) Ar atoms discussed earlier, it might be acceptable to use the \(3N\) Cartesian coordinates of the \(N\) atoms. However, for the water example, it would be very inefficient to employ the \(9N\) Cartesian coordinates of the \(N\) water molecules. Displacement of, for example, one of the \(H\) atoms along the x-axis while keeping all other coordinates fixed would alter the intramolecular O-H bond energy and the H-O-H bending energy as well as the intermolecular hydrogen bonding energies to neighboring water molecules. The intramolecular energy changes would likely be far in excess of \(kT\) unless a very small coordinate change \(\delta q\) were employed. Because it is important to the efficiency of the MC process to make displacements \(\delta q\) that produce ca. 50% acceptance, it is better, for the water case, to make use of coordinates such as the center of mass and orientation coordinates of the water molecules (for which larger displacements produce energy changes within a few \(kT\)) and smaller displacements of the O-H stretching and H-O-H bending coordinates (to keep the energy change within a few \(kT\)).
Another point to make about how the MC process is often used is that, when the inter-molecular energy is pair wise additive, evaluation of the energy change \(V(q+\delta q) – V(q) = \delta V\) accompanying the change in \(q\) requires computational effort that is proportional to the number \(N\) of molecules in the system because only those factors \(V_{\rm (intermolecular)}{}_{J,K}\), with \(J\) or \(K\) equal to the single molecule that is displaced need be computed. This is why pair wise additive forms for \(V\) are often employed.
Let us now return to how the MC process is implemented. If the energy change \(\delta V\) is negative (i.e., if the potential energy is lowered by the coordinate displacement), the change in coordinate \(\delta q\) is allowed to occur and the resulting new configuration is counted among the MC-accepted configurations. On the other hand, if \(\delta V\) is positive, the move from \(q\) to \(q + \delta q\) is not simply rejected (to do so would produce an algorithm directed toward finding a minimum on the energy landscape, which is not the goal). Instead, the quantity \(P = \exp(-\delta V/kT)\) is used to compute the probability for accepting this energy-increasing move. In particular, a random number between, for example, 0.000 and 1.000 is selected. If the random number is greater than \(P\) (expressed in the same decimal format), then the move is rejected. If the random number is less than \(P\), the move is accepted and the new location is included among the set of MC-accepted configurations. Then, new water molecule and its internal or external coordinate are chosen at random and the entire process is repeated.
In this manner, one generates a sequence of MC-accepted moves representing a series of configurations for the system of \(N\) water molecules. Sometimes this series of configurations is called a Monte Carlo trajectory, but it is important to realize that there is no dynamics or time information in this series. This set of configurations has been shown to be properly representative of the geometries that the system will experience as it moves around at equilibrium at the specified temperature \(T\) (n.b., \(T\) is the only way that information about the molecules' kinetic energy enters the MC process), but no time or dynamical attributes are contained in it.
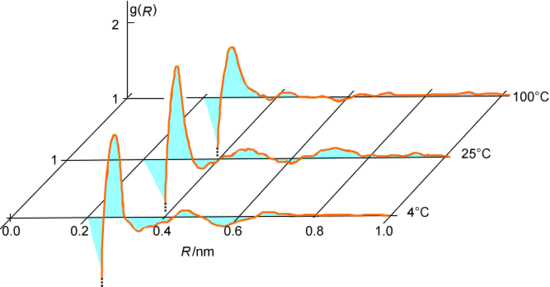
As the series of accepted steps is generated, one can keep track of various geometrical and energetic data for each accepted configuration. For example, one can monitor the distances R among all pairs of oxygen atoms in the water system being discussed and then average this data over all of the accepted steps to generate an oxygen-oxygen radial distribution function \(g(R)\) as shown in Figure 7.3. Alternatively, one might accumulate the intermolecular interaction energies between pairs of water molecules and average this over all accepted configurations to extract the cohesive energy of the liquid water.
The MC procedure also allows us to compute the equilibrium average of any property \(A(q)\) that depends on the coordinates of the \(N\) molecules. Such an average would be written in terms of the normalized coordinate probability distribution function \(P(q)\) as:
\[\langle A \rangle = \int P(q)A(q) dq = \dfrac{\int \exp(-\beta V(q))A(q)dq}{\int \exp(-\beta V(q))dq}\]
The denominator in the definition of \(P(q)\) is, of course, proportional to the coordinate-contribution to the partition function \(Q\). In the MC process, this average is computed by forming the following sum over the M MC-accepted configurations \(q_J\):
\[\langle A \rangle =\frac{1}{M}\sum_{J=1}^M A(q_J)\]
In most MC simulations, millions of accepted steps contribute to the above averages. At first glance, it may seem that such a large number of steps represent an extreme computational burden. However, recall that straightforward discretization of the \(3N\) axes produced a result whose effort scaled as \(K^{3N}\), which is unfeasible even for small numbers of molecules
So, why do MC simulations work when the straightforward way fails? That is, how can one handle thousands or millions of coordinates when the above analysis would suggest that performing an integral over so many coordinates would require \(K^{3N}\) computations? The main thing to understand is that the \(K\)-site discretization of the \(3N\) coordinates is a stupid way to perform the above integral because there are many (in fact, most) coordinate values where the value of the quantity A whose average one wants multiplied by \(\exp(-\beta V)\) is negligible. On the other hand, the MC algorithm is designed to select (as accepted steps) those coordinates for which \(\exp(-\beta V)\) is non-negligible. So, it avoids configurations that are stupid and focuses on those for which the probability factor is largest. This is why the MC method works!
The standard Metropolis variant of the MC procedure was described above where its rules for accepting or rejecting trial coordinate displacements \(\delta q\) were given. There are several other ways of defining rules for accepting or rejecting trial MC coordinate displacements, some of which involve using information about the forces acting on the coordinates, all of which can be shown to generate a series of MC-accepted configurations consistent with an equilibrium system. The book Computer Simulations of Liquids, M. P. Allen and D. J. Tildesley, Oxford U. Press, New York (1997) provides good descriptions of these alternatives to the Metropolis MC method, so I will not go further into these approaches here.
Umbrella Sampling
It turns out that the MC procedure as outlined above is a highly efficient method for computing multidimensional integrals of the form
\[\int P(q) A(q) dq\]
where \(P(q)\) is a normalized (positive) probability distribution and \(A(q)\) is any property that depends on the multidimensional variable q.
There are, however, cases where this conventional MC approach needs to be modified by using so-called umbrella sampling. To illustrate how this is done and why it is needed, suppose that one wanted to use the MC process to compute an average, with \(\exp(-\beta V(q))\) as the weighting factor, of a function \(A(q)\) that is large whenever two or more molecules have high (i.e., repulsive) intermolecular potentials. For example, one could have
\[A(q) = \sum_{I<J} \frac{a}{|\textbf{R}_I- \textbf{R}_J|^n}.\]
Such a function could, for example, be used to monitor when pairs of molecules, with center-of-mass coordinates RJ and RI, approach closely enough to undergo a reaction that requires them to surmount a high inter-molecular barrier.
The problem with using conventional MC methods to compute
\[\langle A \rangle = \int A(q) P(q) dq\]
in such cases is that
- i. \(P(q) = \dfrac{\exp(-\beta V(q))}{\int \exp(-\beta V)dq}\) favors those coordinates for which the total potential energy \(V\) is low. So, coordinates with high \(V(q)\) are very infrequently accepted.
- ii. However, \(A(q)\) is designed to identify events in which pairs of molecules approach closely and thus have high \(V(q)\) values.
So, there is a competition between \(P(q)\) and \(A(q)\) that renders the MC procedure ineffective in such cases because the average one wants to compute involves the product \(A(q) P(q)\) which is small for most values of q.
What is done to overcome this competition is to introduce a so-called umbrella weighting function \(U(q)\) that
- i. attains it largest values where \(A(q)\) is large, and
- ii. is positive and takes on values between 0 and 1 so it can be used as shown below to define a proper probability weighting function.
One then replaces \(P(q)\) in the MC algorithm by the product \(P(q)U(q)\) and uses this as a weighting function. To see how this replacement works, we re-write the average that needs to be computed as follows:
\[\langle A \rangle = \int P(q)A(q) dq = \dfrac{\int \exp(-\beta V(q))A(q)dq}{\int \exp(-\beta V(q))dq}\]
\[=\dfrac{\dfrac{ \int U(q)\exp(-\beta V(q))(A(q)/U(q)) dq }{\int U(q)\exp(-\beta V(q)) dq}}{\dfrac{ \int U(q)\exp(-\beta V(q))(1/U(q)) dq}{ \int U(q)\exp(-\beta V(q)) dq}}=\dfrac{\Big\langle \dfrac{A}{U}\Big\rangle_{Ue^{-\beta UV}}}{\Big\langle \dfrac{1}{U}\Big\rangle_{Ue^{-\beta V}}}\]
The interpretation of the last identity is that \(\langle A \rangle \) can be computed by
- i. using the MC process to evaluate the average of (\(A(q)/U(q)\)) but with a probability weighting factor of \(U(q) \exp(-\beta V(q))\) to accept or reject coordinate changes, and
- ii. also using the MC process to evaluate the average of (\(1/U\)(q)) again with \(U(q) \exp(-\beta V(q))\) as the weighting factor, and finally
- iii. taking the average of (\(A/U\)) divided by the average of (\(1/U\)) to obtain the final result.
The secret to the success of umbrella sampling is that the product
\(U(q) \exp(-\beta V(q))\) causes the MC process to emphasize in its acceptance and rejection procedure coordinates for which both \(\exp(-\beta V)\) and \(U\) (and hence \(A\)) are significant. Of course, the tradeoff is that the quantities (\(A/U\) and \(1/U\)) whose averages one computes using \(U(q) \exp(-\beta V(q))\) as the MC weighting function are themselves susceptible to being very small at coordinates \(q\) where the weighting function is large. Let’s consider some examples of when and how one might want to use umbrella sampling techniques.
Suppose one has one system for which the evaluation of the partition function (and thus all thermodynamic properties) can be carried out with reasonable computational effort and another similar system (i.e., one whose potential does not differ much from the first) for which this task is very difficult. Let’s call the potential function of the first system \(V^0\) and that of the second system \(V^0 + \Delta V\). The latter system’s partition function can be written as follows
\[Q=\sum_J \exp(-\beta (V^0+\Delta V))=Q^0 \sum_J \exp(-\beta(V^0+\Delta V))/Q^0=Q^0\langle \exp(-\beta(V^0+\Delta V))\rangle^0\]
where \(Q^0\) is the partition function of the first system and is the ensemble average of the quantity taken with respect to the ensemble appropriate to the first system. This result suggests that one can form the ratio of the partition functions (\(Q/Q^0\)) by computing the ensemble average of using the first system’s weighting function in the MC process. Likewise, to compute, for second system, the average value of any property \(A(q)\) that depends only on the coordinates of the particles, one can proceed as follows
\[\langle A \rangle=\dfrac{\sum_J A_J\exp(-\beta(V^0+\Delta V)) }{Q}=\frac{Q^0}{Q}\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0\]
where is the ensemble average of the quantity \(A\) taken with respect to the ensemble appropriate to the first system. Using the result derived earlier for the ratio (\(Q/Q^0\)), this expression for \(\langle A \rangle \) can be rewritten as
\[\langle A \rangle=\frac{Q^0}{Q}\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0=\dfrac{\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0}{\langle \exp(-\beta(V^0+\Delta V)) \rangle^0}.\]
In this form, we are instructed to form the average of \(A\exp(-\beta(V^0+\Delta V))\) for the second system by
- a. forming the ensemble average of using the weighting function for the first system,
- b. forming the ensemble average of using the weighting function for the first system, and
- c. taking the ratio of these two averages.
This is exactly what the umbrella sampling device tells us to do if we were to choose as the umbrella function
\[U=\exp(\beta \Delta V).\]
In this example, the umbrella is related to the difference in the potential energies of the two systems whose relationship we wish to exploit.
Under what circumstances would this kind of approach be useful? Suppose one were interested in performing a MC average of a property for a system whose energy landscape \(V(q)\) has many local minima separated by large energy barriers, and suppose it was important to sample configurations characterizing the many local minima in the sampling. A straightforward MC calculation using \(\exp(-\beta V)\) as the weighting function would likely fail because a sequence of coordinate displacements from near one local minimum to another local minimum would have very little chance of being accepted in the MC process because the barriers are very high. As a result, the MC average would likely generate configurations representative of only the system’s equilibrium existence near one local minimum rather than representative of its exploration of the full energy landscape.
However, if one could identify those regions of coordinate space at which high barriers occur and construct a function \(\Delta V\) that is large and positive only in those regions, one could then use
\[U=\exp(\beta \Delta V).\]
as the umbrella function and compute averages for the system having potential \(V(q)\) in terms of ensemble averages for a modified system whose potential \(V_0\) is
\[V^0=V-\Delta V\]
In Figure 7. 3a, I illustrate how the original and modified potential landscapes differ in regions between two local minima.
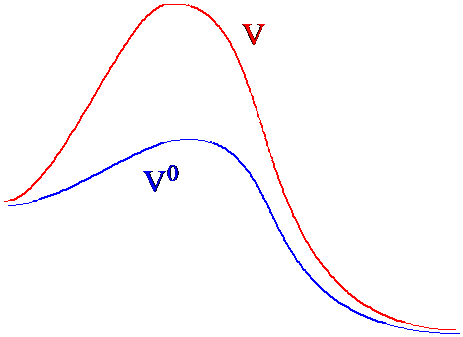
The MC-accepted coordinates generated using the modified potential \(V^0\) would sample the various local minima and thus the entire landscape in a much more efficient manner because they would not be trapped by the large energy barriers. By using these MC-accepted coordinates, one can then estimate the average value of a property \(A\) appropriate to the potential \(V\) having the large barriers by making use of the identity.
\[\langle A \rangle=\frac{Q^0}{Q}\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0=\dfrac{\langle A\exp(-\beta(V^0+\Delta V)) \rangle^0}{\langle \exp(-\beta(V^0+\Delta V)) \rangle^0}.\]
The above umbrella strategy could be useful in generating a good sampling of configurations characteristic of the many local minima, which would be especially beneficial if the quantity \(A(q)\) emphasized those configurations. This would be the case, for example, if \(A(q)\) measured the intramolecular and nearest-neighbor oxygen-hydrogen interatomic distances in a MC simulation of liquid water. On the other hand, if one wanted to use as \(A(q)\) a measure of the energy needed for a \(Cl^-\) ion to undergo, in a 1 M aqueous solution of NaCl, a change in coordination number from 6 to 5 as illustrated in Figure 7.3 b, one would need a sampling that is accurate both near the local minima corresponding to the 5- and 6-coordinate and the transition-state structures.
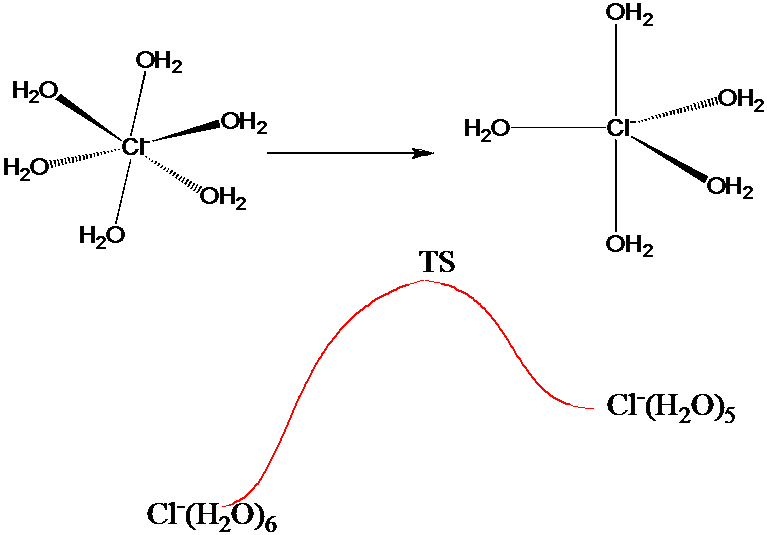
Using an umbrella function similar to that discussed earlier to simply lower the barrier connecting the two \(Cl^-\) ion structures may not be sufficient. Although this would allow one to sample both local minima, its sampling of structures near the transition state would be questionable if the quantity \(\Delta V\) by which the barrier is lowered (to allow MC steps moving over the barrier to be accepted with non-negligible probability) is large. In such cases, it is wise to employ a series of umbrellas to connect the local minima to the transition states.
Assuming that one has knowledge of the energies and local solvation geometries characterizing the two local minima and the transition state as well as a reasonable guess or approximation of the intrinsic reaction path (refer back to Section 3.3 of Chapter 3) connecting these structures, one proceeds as follows to generate a series of so-called windows within each of which the free energy \(A\) of the solvated \(Cl^-\) ion is evaluated.
- 1. Using the full potential \(V\) of the system to constitute the unaltered weighting function \(\exp(-\beta V(q))\), one multiplies this by an umbrella function \[U(q)=\dfrac{0;\{s_1-\delta/2\le s(q)\le s_1+\delta/2\}}{\infty;{\rm otherwise}}\]
to form the umbrella-altered weighting function \(U(q) \exp(-\beta V(q))\). In U(q), s(q) is the value of the value of the intrinsic reaction coordinate IRC evaluated for the current geometry of the system q, \(s_1\) is the value of the IRC characterizing the first window, and d is the width of this window. The first window could, for example, correspond to geometries near the 6-coordinate local minimum of the solvated \(Cl^-\) ion structure. The width of each window d should be chosen so that the energy variation within the window is no more than a 1-2 kT; in this way, the MC process will have a good (i.e., ca. 50%) acceptance fraction and the configurations generated will allow for energy fluctuations uphill toward the TS of about this amount. - 2. As the MC process is performed using the above \(U(q) \exp(-\beta V(q))\) weighting, one constructs a histogram \(P_1(s)\) for how often the system reaches various values s along the IRC. Of course, the severe weighting caused by \(U(q)\) will not allow the system to realize any value of s outside of the window .
- 3. One then creates a second window that connects to the first window (i.e., with \(s_1+\delta/2 = s_2 - \delta/2\)) and repeats the MC sampling using \[U(q)=\dfrac{0;\{s_2-\delta/2\le s(q)\le s_2+\delta/2\}}{\infty;{\rm otherwise}}\]
to generate a second histogram \(P_2(s)\) for how often the system reaches various values of s along the IRC within the second window. - 4. This process is repeated at a series of connected windows \(\{s_k-\delta/2\le s(q)\le s_k+\delta/2\}\)
whose centers \(s_k\) range from the 6-coordinate \(Cl^-\) ion (\(k = 1\)), through the transition state (\(k = TS\)), and to the 5-coordinate \(Cl^-\) ion (\(k = N\)).
After performing this series of \(N\) umbrella-altered samplings, one has in hand a series of \(N\) histograms {\(P_k(s); k = 1, 2, \cdots TS, \cdots N\)}. Within the \(k^{\rm th}\) window, \(P_k(s)\) gives the relative probability of the system being at a point s along the IRC. To generate the normalized absolute probability function P(s) expressing the probability of being at a point s, one can proceed as follows:
1. Because the first and second windows are connected at the point \(s_1+\delta/2 = s_2 - \delta/2\), one can scale \(P_2(s)\) (i.e., multiply it by a constant) to match \(P_1(s)\) at this common point to produce a new \(P'_2(s)\) function
\[P'_2(s)=P_2(s)\dfrac{P_1(s_1+\delta/2)}{P_2(s_2-\delta/2)}\]
This new function describes exactly the same relative probability within the second window, but, unlike \(P_2(s)\), it connects smoothly to \(P_1(s)\).
2. Because the second and third windows are connected at the point \(s_2+\delta/2 = s_3 - \delta/2\), one can scale \(P_3(s)\) to match at this common point to produce a new function
\[P'_3(s)=P_3(s)\dfrac{P'_2(s_2+\delta/2)}{P_3(s_3-\delta/2)}\]
3. This process of scaling \(P_k\) to match at \(s_k – \delta/2 = s_{k-1} + \delta/2\) is repeated until the final window connecting \(k = N-1\) to \(k = N\). Upon completing this series of connections, one has in hand a continuous probability function \(P(s)\), which can be normalized
\[P_{\rm normalized}=\frac{P(s)}{\int_{s=0}^{s_{\rm final}}P(s)ds }\]
In this way, one can compute the probability of accessing the TS, \(P_{\rm normalized}(s=TS)\), and the free energy profile
\[A(s)=-kT\ln P_{\rm normalized}(s)\]
at any point along the IRC. It is by using a series of connected windows, within each of which the MC process samples structures whose energies can fluctuate by 1-2 \(kT\), that one generates a smooth connection from low-energy to high-energy (e.g., TS) geometries.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry
Integrated by Tomoyuki Hayashi (UC Davis)


