4.6: Time Dependent Perturbation Theory
- Page ID
- 11584
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)When dealing with the effects of external perturbations (e.g., applied fields, collisions with other species), one needs to have a way to estimate the probabilities and rates of transitions among states of the system of interest induced by these perturbations. Time-dependent perturbation theory (TDPT) offers a framework within which such estimates can be achieved.
Derivation
In deriving the working equations of TDPT, one begins with the time-dependent Schrödinger equation
\[i\hbar \frac{\partial \Psi}{\partial t}=[H_0+V(t)]\Psi \label{1}\]
in which \(H_0\) is the Hamiltonian for the system whose transitions are to be probed, and \(V(t)\) is the perturbation caused by the external field or the collision. The wave function that solves this equation is expanded in an order-by-order manner as in conventional perturbation theory
\[\Psi=\psi^{(0)}(r)\exp\Big(-it\frac{E^{(0)}}{\hbar}\Big)+\psi^{(1)}+\cdots \label{2}\]
Here \(\psi_0\) is the eigenfunction of \(H_0\) from which transitions to other eigenstates (denoted ) of \(H_0\) are being considered. Because, in the absence of the external perturbation \(V(t)\), the states of \(H_0\) are known to vary with time as , this component of the time dependence of the total wave function is included in the above expansion. Then, the first-order correction \(\psi^{(1)}\) is expanded in terms of the complete set of states { } after which the expansion coefficients { } become the unknowns to be solved for
\[\psi^{(1)}=\sum_f \psi^{(0)}_f(r)\exp\bigg(-it\frac{E^{(0)}_f}{\hbar}\bigg)C^{(1)}_f(t). \label{3}\]
It should be noted that this derivation treats the zeroth-order states {\(\psi^{(0)}\) and \(\psi^{(0)}_f\)} as eigenfunctions of \(H_0\). However, in most practical applications of TDPT, {\(\psi^{(0)}\) and \(\psi^{(0)}_f\)} are not known exactly and, in fact, are usually approximated by using variational or perturbative methods (e.g., to treat differences between HF mean-field and true Coulombic interactions among electrons). So, the derivation of TDPT that we are pursuing assumes the {\(\psi^{(0)}\) and \(\psi^{(0)}_f\)} are exact eigenfunctions. When the final TDPT working equations are thus obtained, one usually substitutes perturbative or variational approximations to {\(\psi^{(0)}\) and \(\psi^{(0)}_f\)} into these equations.
Substituting the order-by-order expansion into the Schrödinger equation gives, for the left- and right-hand sides,
\[i\hbar \frac{\partial \Psi}{\partial t} = E^{(0)}\psi^{(0)}(r)\exp\Big(-it\frac{E^{(0)}}{\hbar}\Big)\\
+ \sum_f \left[ E^{(0)}_f\psi^{(0)}_f(r)\exp\bigg(-it\frac{E^{(0)}_f}{\hbar}\bigg)C^{(1)}_f(t)
-i\hbar\psi^{(0)}_f(r)\exp\bigg(-it\frac{E^{(0)}_f}{\hbar}\bigg)\frac{C^{(1)}_f(t)}{dt} \right] \label{4a}\]
and
\[[H_0+V(t)]\Psi=E^{(0)}\psi^{(0)}(r)\exp\Big(-it\frac{E^{(0)}}{\hbar}\Big)\\
+\sum_f E^{(0)}_f\psi^{(0)}_f(r)\exp\bigg(-it\frac{E^{(0)}_f}{\hbar}\bigg)C^{(1)}_f(t)
+V(t)\psi^{(0)}(r)\exp\Big(-it\frac{E^{(0)}}{\hbar}\Big), \label{4b}\]
respectively, through first-order. Multiplying each of these equations on the left by the complex conjugate of a particular \(\psi_f^0\) and integrating over the variables that \(H_0\) depends on produces the following equation for the unknown first-order coefficients
\[-i\hbar\frac{dC^{(1)}_f(t)}{dt}=\langle \psi^{(0)}_f|V(t)|\psi^{(0)}_f \rangle \exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg). \label{5}\]
The states and can be different electronic states, vibrational states, or rotational states. In Chapter 15 of my book Quantum Mechanics in Chemistry referred to in Chapter 1, I treat each of these types of transitions in detail. In the present discussion, I will limit myself to the general picture of TDPT, rather than focusing on any of these particular forms of spectroscopic transitions.
To proceed further, one needs to say something about how the perturbation \(V(t)\) depends on time. In the most common application of TDPT, the perturbation is assumed to consist of a term that depends on spatial variables (denoted \(v(r)\)) multiplied by a time-dependent factor of sinusoidal character. An example of such a perturbation is provided by the electric dipole potential
\[V(t)=\textbf{E}\cdot [ e\sum_n Z_n \textbf{R}_n - e \sum_i \textbf{r}_i ]\cos(\omega t)\]
characterizing photons of frequency \(\omega\) interacting with the nuclei and electrons of a molecule. \(\textbf{E}\cdot [ e\sum_n Z_n \textbf{R}_n - e \sum_i \textbf{r}_i ]\) is the spatial part \(v(\textbf{r})\) and \(\cos(\omega t)\) is the time-dependence.
To allow for the possibility that photons over a range of frequencies may impinge on the molecules, we can proceed with the derivation for photons of a given frequency \(\omega\) and, after obtaining our final result, average over a distribution of frequencies characterized by a function \(f(\omega)\) giving the number of photons with frequencies between \(\omega\) and \(\omega+d\omega\). For perturbations that do not vary in a sinusoidal manner (e.g., a perturbation arising from a collision with another molecule), the derivation follows a different path at this point (application 3 below). Because spectroscopic time-dependent perturbations are extremely common in chemistry, we will focus much of our attention to this class of perturbations in this Chapter.
To proceed deriving the working equations of TDPT, the above expression for \(V(t)\) is inserted into the differential equation for the expansion coefficients and the equation is integrated from an initial time \(t_i\) to a final time \(t_f\). These times describe when the external perturbation is first turned on and when it is turned off, respectively. For example, a laser whose photon intensity profile is described by \(f(\omega)\) might be pulsed on from \(t_i\) to \(t_f\), and one wants to know what fraction of the molecules initially in \(\psi_0\) have undergone transitions to each of the . Alternatively, the molecules may be flowing in a stream that passes through a laser light source that is continually on, entering the laser beam at \(t_i\) and exiting from the laser beam at \(t_f\). In either case, the molecules would be exposed to the photons from \(t_i\) until \(t_f\). The result of integrating the differential equation is
\[\begin{split}C^{(1)}_f(t)&=\frac{-1}{2i\hbar}\int_{t_i}^{t_f}\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r) \rangle
[\exp(i\omega t)+\exp(-i\omega t)]\exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg)\\
&=\frac{-1}{2i\hbar}\int_{t_i}^{t_f}\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r) \rangle
[\exp(i(\omega+\omega_{f,0}) t)+\exp(-i(\omega-\omega_{f,0}) t)]\\
&=\frac{-1}{2i\hbar}\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r) \rangle\\
&\times\left[\frac{\exp(i(\omega+\omega_{f,0}) t_f-\exp(i(\omega+\omega_{f,0}) t_i))}{i(\omega+\omega_{f,0})}
+\frac{\exp(-i(\omega-\omega_{f,0}) t_f-\exp(-i(\omega-\omega_{f,0}) t_i))}{i(\omega-\omega_{f,0})}
\right]\end{split} \label{6}\]
where the transition frequencies \(\omega_{f,0}\) are defined by
\[\omega_{f,0}=\frac{(E^{(0)}-E^{(0)}_f)}{\hbar} \label{7}\]
and \(t\) is the time interval \(t_f –t_i\).
Now, if the frequency \(\omega\) is close to one of the transition frequencies, the term with \((\omega-\omega_{f,0})\) in the denominator will be larger than the term containing \((\omega-\omega_{f,0})\). Of course, if has a higher energy than , so one is studying stimulate emission spectroscopy, \(\omega_{f,0}\) will be negative, in which case the term containing \((\omega+\omega_{f,0})\) will dominate. In on-resonance absorption spectroscopy conditions, the above expression for the first-order coefficients reduces to
\[C^{(1)}_f(t)=\frac{-1}{2i\hbar}\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle
\frac{\exp(-i(\omega-\omega_{f,0}) t_f-\exp(-i(\omega-\omega_{f,0}) t_i))}{i(\omega-\omega_{f,0})}. \label{8}\]
The modulus squared of this quantity gives a measure of the probability of observing the system in state after being subjected to the photons of frequency \(\omega\) for a length of time \(t\).
\[|C^{(1)}_f(t)|^2=\frac{|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}
\frac{2[1-\cos((\omega-\omega_{f,0})t)]}{(\omega-\omega_{f,0})^2}\\
=\frac{|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2} \frac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}
. \label{9}\]
The function \(\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}\) is plotted in Figure 4.4 for a given value of \(t\) as a function of \(\omega\). It is sharply peaked around \(\omega = \omega_{f,0}\), decays rapidly as \(|(\omega - \omega_{f,0})|\) increases, and displays recurrences of smaller and smaller intensity when \((\omega - \omega_{f,0})t\) passes through multiples of \(\pi\).
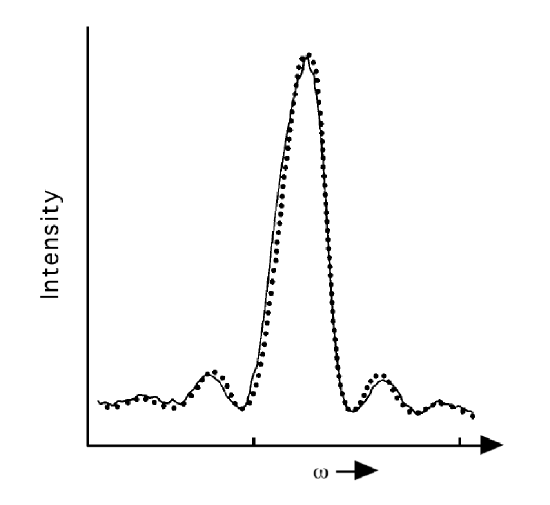
At larger values of \(t\), the main peak in the plot of this function becomes narrower and higher such that, in the \(t \rightarrow \infty\) limit, the area under this plot approaches \(t\pi/2\):
\[{\rm Area}=\int\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}d\omega=t\frac{\pi}{2}. \label{10}\]
The importance of this observation about the area under the plot shown in Figure 4.4 can be appreciated by returning to our result
\[|C^{(1)}_f(t)|^2= \frac{|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2} \frac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2} \label{11}\]
and introducing the fact that the photon source used to induce the transitions being studied most likely is not perfectly monochromatic. If it is characterized, as suggested earlier, by a distribution of frequencies \(f(\omega)\) that is broader than the width of the large central peak in Figure 4.4 (n.b., this will be true if the time duration \(t\) is long enough), then when we average over \(f(\omega)\) to obtain a result that directly relates to this kind of experiment, we obtain
\[\int_{-\infty}^\infty f(\omega)|C^{(1)}_f(t)|^2d\omega
=\frac{|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2} \int_{-\infty}^\infty f(\omega)\frac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}d\omega\\
\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2t}{4\hbar^2}f(\omega_{f,0})=\langle |C^{(1)}_f(t)|^2 \rangle
\label{12}\]
We are allowed to write the integral over \(\omega\) as ranging from \(-\infty\) to \(+\infty\) because the function shown in Figure 4.4 is so sharply peaked around \(\omega_{f,0}\) that extending the range of integration makes no difference. We are allowed to factor the \(f(\omega)\) out of the integral as f(\(\omega_{f,0}\)) by assuming the light source’s distribution function \(f(\omega)\) is very smoothly varying (i.e., not changing much) in the narrow range of frequencies around \(\omega_{f,0}\) where the function in Figure 4.4 is sharply peaked.
The result of this derivation of TDPT is the above expression for the average probability of observing a transition from state \(\psi_0\) to state . This probability is seen to grow linearly with the time duration over which the system is exposed to the light source. Because we carried out this derivation within first-order perturbation theory, we should trust this result only under conditions where the effects of the perturbation are small. In the context of the example considered here, this means only for short times. That is, we should view
\[\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2t}{4\hbar^2}f(\omega_{f,0})=\langle |C^{(1)}_f(t)|^2 \rangle \label{13}\]
as expressing the short-time estimate of the probability of a transition from \(\psi_0\) to and
\[{\rm Rate}=\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,0})\]
(obtained as \(\dfrac{d\langle |C^{(1)}_f(t)|^2 \rangle}{dt}\)) as expressing the initial rate of such transitions within the first-order TDPT approximation.
It should be noted that the rate expression given above will not be valid if the time duration t of the perturbation does not obey \(\omega_{f,o} t \gg p\); only when this condition is met an the function shown in Figure 4.4 be integrated to generate a probability prediction that grows linearly with time. So, one has to be careful when using pulsed lasers of very short duration to not employ the simplified rate expression given above (e.g., 1 eV corresponds to a frequency of ca. 2.4 x1014 s-1, so to study an electronic transition of this energy, one needs to use a light source of duration significantly longer than \(10^{-14}\) s to make use of the simplified result).
The working equations of TDPT, given above, allow one to estimate (because this is a first-order theory) the rates of transitions from one quantum state to another induced by a perturbation whose spatial dependence is characterized by \(v(r)\) and whose time dependence is sinusoidal. The same kind of coupling matrix elements \(\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle\) as we experienced in time-independent PT govern the selection rules and intensities for these transitions, so there is no need to repeat how symmetry can be used to analyze these integrals.
Before closing this treatment of TDPT, it is useful to address a few issues that were circumvented in the derivation presented above.
Application 1: Coupling to a Continuum
In some cases, one is interested in transitions from a particular initial state \(\psi^{(0)}(r)\) into a manifold of states that exist in a continuum having energies between \(E^{(0)}_f\) and \(E^{(0)}_f+dE^{(0)}_f\). This occurs, for example, when treating photoionization of a neutral or photodetachment of an anion; here the ejected electron exists in a continuum wave function whose density of states \(\rho(E^{(0)}_f)\) is given by the formulas discussed in Chapter 2. In such cases, the expression given above for the rate is modified by summing over all final states having energies within \(E^{(0)}_f\) and \(E^{(0)}_f+dE^{(0)}_f\). Returning to the earlier expression
\[\int\rho(E^{(0)}_f)\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}
\int_{-\infty}^\infty f(\omega)\frac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}d\omega dE^{(0)}_f \label{14}\]
using \( dE^{(0)}_f=\hbar\omega_{f,0}\), and assuming the matrix elements \(\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle\) do not vary significantly within the narrow range between and , one arrives at a rate expression of
\[{\rm Rate}=\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,0})\rho(E^{(0)}_f) \label{15}\]
which is much like we obtained earlier but now contains the density of states \(\rho(E^{(0)}_f)\). In some experiments, one may not have only a single state \(\psi^{(0)}_f(r)\) that can absorb light of a given frequency w; in such a situation, attenuation of the light source at this frequency can occur through absorptions from many initial states \(\psi^{(0)}_f(r)\) into all possible final states whose energy differs from that of the initial state by . In this case, the correct expression for the total rate of absorption of photons of energy is obtained by averaging the above result over the probabilities \(P_i\) of the system being in various initial states (which we label \(\psi^{(0)}_i\)):
\[{\rm Rate}=\sum_i P_i \frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,i})\rho(E^{(0)}_f)\delta(\omega-\omega_{f,i}). \label{16}\]
Here the \(\delta(\omega-\omega_{f,i})\) function guarantees that only states \(\psi^{(0)}_i\) and \(\psi^{(0)}_f\) whose energies differ by are permitted to enter the sum. The nature of the initial-state probability \(P_i\) depends on what kind of experiment is being carried out. \(P_i\) might be a Boltzmann distribution if the initial states are in thermal equilibrium, for example.
Application 2: Experimental Oscillations
In Figure 4.4 the function \(\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}\) is plotted for one value of \(t\) as a function of \(\omega\). There also appear in this figure, dots that represent experimental data. These data were obtained by allowing a stream of \(HCN\) molecules to flow through a laser beam of width \(L\) with the laser frequency tuned to \(\omega\). From the flow velocity \(v\) of the \(HCN\) stream and the laser beam width \(L\), one can determine the duration over which the molecules were exposed to the light source \(t = \dfrac{L}{v}\). After the molecules exited the laser beam, they were probed to determine whether they were in an excited state. This experiment was repeated for various values of the frequency \(\omega\). The population of excited states was then plotted as a function of \(\omega\) to obtain the data plotted in Figure 4.4. This experiment is described in the text Molecules and Radiation, J. I. Steinfeld, MIT Press, Cambridge, Mass. (1981). This kind of experiment provided direct proof of the oscillatory frequency dependence observed in the population of excited states as predicted in our derivation of TDPT.
Application 3: Collisionally induced Transitions
To give an example of how one proceeds in TDPT when the perturbation is not oscillatory in time, let us consider an atom located at the origin of our coordinate system that experiences a collision with an ion of charge c whose trajectory is described in Figure 4.5.

As an approximation, we assume
- that the ion moves in a straight line: \(= vt, Y = D, Z = 0\), characterized by an impact parameter \(D\) and a velocity \(v\) (this would be appropriate if the ion were moving so fast that it would not be deflected by interactions with the atom),
- that the perturbation caused by the ion on the electrons of the atom at the origin can be represented by
\[-\sum_{i=1}^N\frac{\chi}{|\textbf{r}_i-\textbf{R}|} \label{17}\]
where \(\textbf{r}_i\) is the position of the ith electron in the atom and \(\textbf{R} = (vt, D, 0)\) is the position of the ion. The time dependence of the perturbation arises from the motion of the ion along the \(X\)-axis.
Writing the distance \(|\textbf{r}_i-\textbf{R}|\) as
\[|\textbf{r}_i-\textbf{R}|=\sqrt{(x_i-vt)^2+(y_i-D)^2+z_i^2} \label{18}\]
and expanding in inverse powers of \(\sqrt{D^2+(vt)^2}\) we can express the ion-atom interaction potential as
\[-\sum_{i=1}^N\frac{\chi}{|r_i-R|}=\sum_i^N\left[\frac{-\chi}{\sqrt{D^2+(vt)^2}}+\frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}+\cdots\right]. \label{19}\]
The first term contains no factors dependent on the atom’s electronic coordinates, so it plays no role in causing electronic transitions. In the second term, the factor \(r_i^2\) can be neglected compared to \(vtx_i+Dy_i\) the terms because the ion is assumed to be somewhat distant from the atom’s valence electrons.
To derive an equation for the probability of the atom undergoing a transition from \(\psi^{(0)}(r)\) to \(\psi^{(0)}_f(r)\), one returns to the TDPT expression
\[-i\hbar\frac{dC^{(1)}_f(t)}{dt}=\langle \psi^{(0)}_f|V(t)|\psi^{(0)}(r)\rangle\exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg) \label{20}\]
and substitutes the above expression for the perturbation to obtain
\[\frac{dC^{(1)}_f(t)}{dt}=\frac{-1}{i\hbar} \langle \psi^{(0)}_f|\sum_{i=1}^N \frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}|\psi^{(0)}(r)\rangle \exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg). \label{21}\]
This is the equation that must be solved to evaluate by integrating from \(t = -\infty\) to \(t = +\infty\) (representing the full collision with the ion starting far to the left on the \(X\)-axis and proceeding far to the right).
There are two limiting cases in which the solution is straightforward. First, if the time duration of the collision (i.e., the time over which the ion is close to the atom) \(\dfrac{D}{v}\) is long compared to \(\omega_{f,I}\) where
\[\omega_{f,0}=\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}, \label{22}\]
then the integrand will oscillate repeatedly during the time \(\dfrac{D}{v}\) as a result of which the integral
\[C^{(1)}_f(t)=\int_{-\infty}^\infty \frac{dC^{(1)}_f(t)}{dt}dt \label{23}\]
will be vanishingly small. So, in this so-called adiabatic case (i.e., with the ion moving slowly relative to the oscillation frequency \(\omega_{f,0}\)), electronic transitions should not be expected. In the other limit \(\omega_{f,0}\dfrac{D}{v} \ll 1\), the factor \(\exp\bigg(-it\dfrac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg)\) will remain approximately equal to unity, so the integration needed reduces to
\[C^{(1)}_f(t)=\frac{-1}{i\hbar}\int_{-\infty}^\infty\langle\psi^{(0)}_f|\frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}|\psi^{(0)}(r)\rangle dt. \label{24}\]
The integral involving \(vtx_i\)vanishes because \(vt\) is odd and the remainder of the integrand is an even function of \(t\). The integral involving \(Dy_i\) can be performed by trigonometric substitution (\(vt = D \tan\theta\) so the denominator reduces to \(D^3 \Big(1+\Big(\dfrac{\sin\theta}{\cos\theta}\Big)^2\Big)^{3/2} = \dfrac{D^3}{(\cos\theta)^3}\) and gives
\[C^{(1)}_f(t)=\frac{-2\chi}{i\hbar\nu D}\langle\psi^{(0)}_f|\sum_{i=1}^N y_i|\psi^{(0)}(r)\rangle. \label{25}\]
This result suggests that the probability of a transition
\[|C^{(1)}_f(t)|^2=\frac{4\chi^2}{\hbar^2\nu^2 D^2}|\langle\psi^{(0)}_f|\sum_{i=1}^N y_i|\psi^{(0)}(r)\rangle|^2. \label{26}\]
should vary as the square of the ion’s charge and inversely with the speed of the collision. Of course, this result can not be trusted if the speed \(v\) is too low because, then the condition \(\omega_{f,0}\dfrac{D}{v} \ll 1\) will not hold. This example shows how one must re-derive the equations of TDPT when dealing with perturbations whose time-dependence is not sinusoidal.
References
For the reader who wishes a more complete and diverse treatment of TDPT as applied to chemistry, I suggest the text Radiation and Noise in Quantum Electronics, W. H. Louisell, R. E. Krieger, Pub., Huntington, N. Y. (1977) as well as my text Quantum Mechanics in Chemistry.
Contributors and Attributions
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry


