Nuclear Magnetic Resonance Spectroscopy
- Page ID
- 1240
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Over the past fifty years nuclear magnetic resonance spectroscopy, commonly referred to as NMR, has become the preeminent technique for determining the structure of organic compounds. Of all the spectroscopic methods, it is the only one for which a complete analysis and interpretation of the entire spectrum is normally expected. Although larger amounts of sample are needed than for mass spectroscopy, NMR is non-destructive, and with modern instruments good data may be obtained from samples weighing less than a milligram. To be successful in using NMR as an analytical tool, it is necessary to understand the physical principles on which the methods are based.
Introduction
The nuclei of many elemental isotopes have a characteristic spin (I). Some nuclei have integral spins (e.g. I = 1, 2, 3 ....), some have fractional spins (e.g. I = 1/2, 3/2, 5/2 ....), and a few have no spin, I = 0 (e.g. 12C, 16O, 32S, ....). Isotopes of particular interest and use to organic chemists are 1H, 13C, 19F and 31P, all of which have I = 1/2. Since the analysis of this spin state is fairly straight forward, our discussion of NMR will be limited to these and other I = 1/2 nuclei. For a table of nuclear spin characteristics
The following features lead to the NMR phenomenon
1. A spinning charge generates a magnetic field, as shown by the animation on the right. The resulting spin-magnet has a magnetic moment (μ) proportional to the spin.

2. In the presence of an external magnetic field (B0), two spin states exist, +1/2 and -1/2. The magnetic moment of the lower energy +1/2 state is aligned with the external field, but that of the higher energy -1/2 spin state is opposed to the external field. Note that the arrow representing the external field points North.
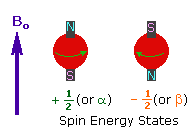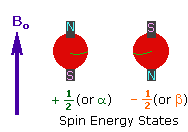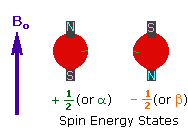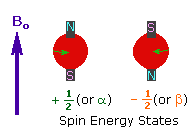
3. The difference in energy between the two spin states is dependent on the external magnetic field strength, and is always very small. The following diagram illustrates that the two spin states have the same energy when the external field is zero, but diverge as the field increases. At a field equal to Bx a formula for the energy difference is given (remember I = 1/2 and μ is the magnetic moment of the nucleus in the field).
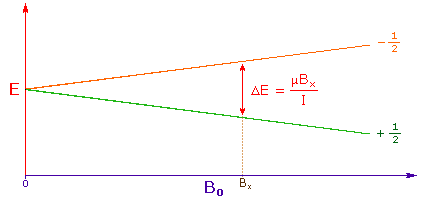
Strong magnetic fields are necessary for NMR spectroscopy. The international unit for magnetic flux is the tesla (T). The earth's magnetic field is not constant, but is approximately 10-4 T at ground level. Modern NMR spectrometers use powerful magnets having fields of 1 to 20 T. Even with these high fields, the energy difference between the two spin states is less than 0.1 cal/mole. To put this in perspective, recall that infrared transitions involve 1 to 10 kcal/mole and electronic transitions are nearly 100 time greater.
For NMR purposes, this small energy difference (ΔE) is usually given as a frequency in units of MHz (106 Hz), ranging from 20 to 900 Mz, depending on the magnetic field strength and the specific nucleus being studied. Irradiation of a sample with radio frequency (rf) energy corresponding exactly to the spin state separation of a specific set of nuclei will cause excitation of those nuclei in the +1/2 state to the higher -1/2 spin state. Note that this electromagnetic radiation falls in the radio and television broadcast spectrum. Nmr spectroscopy is therefore the energetically mildest probe used to examine the structure of molecules.
The nucleus of a hydrogen atom (the proton) has a magnetic moment μ = 2.7927, and has been studied more than any other nucleus. The previous diagram may be changed to display energy differences for the proton spin states (as frequencies) by mouse clicking anywhere within it.
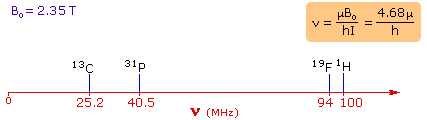
4. For spin 1/2 nuclei the energy difference between the two spin states at a given magnetic field strength will be proportional to their magnetic moments. For the four common nuclei noted above, the magnetic moments are: 1H μ = 2.7927, 19F μ = 2.6273, 31P μ = 1.1305 & 13C μ = 0.7022. These moments are in nuclear magnetons, which are 5.05078•10-27 JT-1. The following diagram gives the approximate frequencies that correspond to the spin state energy separations for each of these nuclei in an external magnetic field of 2.35 T. The formula in the colored box shows the direct correlation of frequency (energy difference) with magnetic moment (h = Planck's constant = 6.626069•10-34 Js).
2. Proton NMR Spectroscopy
This important and well-established application of nuclear magnetic resonance will serve to illustrate some of the novel aspects of this method. To begin with, the NMR spectrometer must be tuned to a specific nucleus, in this case the proton. The actual procedure for obtaining the spectrum varies, but the simplest is referred to as the continuous wave (CW) method. A typical CW-spectrometer is shown in the following diagram. A solution of the sample in a uniform 5 mm glass tube is oriented between the poles of a powerful magnet, and is spun to average any magnetic field variations, as well as tube imperfections. Radio frequency radiation of appropriate energy is broadcast into the sample from an antenna coil (colored red). A receiver coil surrounds the sample tube, and emission of absorbed rf energy is monitored by dedicated electronic devices and a computer. An NMR spectrum is acquired by varying or sweeping the magnetic field over a small range while observing the rf signal from the sample. An equally effective technique is to vary the frequency of the rf radiation while holding the external field constant.
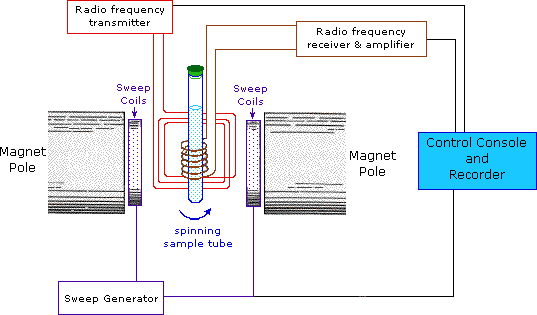

As an example, consider a sample of water in a 2.3487 T external magnetic field, irradiated by 100 MHz radiation. If the magnetic field is smoothly increased to 2.3488 T, the hydrogen nuclei of the water molecules will at some point absorb rf energy and a resonance signal will appear. An animation showing this may be activated by clicking the Show Field Sweep button. The field sweep will be repeated three times, and the resulting resonance trace is colored red. For visibility, the water proton signal displayed in the animation is much broader than it would be in an actual experiment.


Since protons all have the same magnetic moment, we might expect all hydrogen atoms to give resonance signals at the same field / frequency values. Fortunately for chemistry applications, this is not true. By clicking the Show Different Protons button under the diagram, a number of representative proton signals will be displayed over the same magnetic field range. It is not possible, of course, to examine isolated protons in the spectrometer described above; but from independent measurement and calculation it has been determined that a naked proton would resonate at a lower field strength than the nuclei of covalently bonded hydrogens. With the exception of water, chloroform and sulfuric acid, which are examined as liquids, all the other compounds are measured as gases.

Why should the proton nuclei in different compounds behave differently in the NMR experiment ?
The answer to this question lies with the electron(s) surrounding the proton in covalent compounds and ions. Since electrons are charged particles, they move in response to the external magnetic field (Bo) so as to generate a secondary field that opposes the much stronger applied field. This secondary field shields the nucleus from the applied field, so Bo must be increased in order to achieve resonance (absorption of rf energy). As illustrated in the drawing on the right, Bo must be increased to compensate for the induced shielding field. In the upper diagram, those compounds that give resonance signals at the higher field side of the diagram (CH4, HCl, HBr and HI) have proton nuclei that are more shielded than those on the lower field (left) side of the diagram.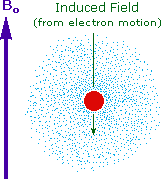
The magnetic field range displayed in the above diagram is very small compared with the actual field strength (only about 0.0042%). It is customary to refer to small increments such as this in units of parts per million (ppm). The difference between 2.3487 T and 2.3488 T is therefore about 42 ppm. Instead of designating a range of NMR signals in terms of magnetic field differences (as above), it is more common to use a frequency scale, even though the spectrometer may operate by sweeping the magnetic field. Using this terminology, we would find that at 2.34 T the proton signals shown above extend over a 4,200 Hz range (for a 100 MHz rf frequency, 42 ppm is 4,200 Hz). Most organic compounds exhibit proton resonances that fall within a 12 ppm range (the shaded area), and it is therefore necessary to use very sensitive and precise spectrometers to resolve structurally distinct sets of hydrogen atoms within this narrow range. In this respect it might be noted that the detection of a part-per-million difference is equivalent to detecting a 1 millimeter difference in distances of 1 kilometer.
Chemical Shift
Unlike infrared and UV-visible spectroscopy, where absorption peaks are uniquely located by a frequency or wavelength, the location of different NMR resonance signals is dependent on both the external magnetic field strength and the rf frequency. Since no two magnets will have exactly the same field, resonance frequencies will vary accordingly and an alternative method for characterizing and specifying the location of NMR signals is needed. This problem is illustrated by the eleven different compounds shown in the following diagram. Although the eleven resonance signals are distinct and well separated, an unambiguous numerical locator cannot be directly assigned to each.

One method of solving this problem is to report the location of an NMR signal in a spectrum relative to a reference signal from a standard compound added to the sample. Such a reference standard should be chemically unreactive, and easily removed from the sample after the measurement. Also, it should give a single sharp NMR signal that does not interfere with the resonances normally observed for organic compounds. Tetramethylsilane, (CH3)4Si, usually referred to as TMS, meets all these characteristics, and has become the reference compound of choice for proton and carbon NMR.
Since the separation (or dispersion) of NMR signals is magnetic field dependent, one additional step must be taken in order to provide an unambiguous location unit. This is illustrated for the acetone, methylene chloride and benzene signals by clicking on the previous diagram. To correct these frequency differences for their field dependence, we divide them by the spectrometer frequency (100 or 500 MHz in the example), as shown in a new display by again clicking on the diagram. The resulting number would be very small, since we are dividing Hz by MHz, so it is multiplied by a million, as shown by the formula in the blue shaded box. Note that νref is the resonant frequency of the reference signal and νsamp is the frequency of the sample signal. This operation gives a locator number called the Chemical Shift, having units of parts-per-million (ppm), and designated by the symbol δ. Chemical shifts for all the compounds in the original display will be presented by a third click on the diagram.
The compounds referred to above share two common characteristics:
• The hydrogen atoms in a given molecule are all structurally equivalent, averaged for fast conformational equilibria.
• The compounds are all liquids, save for neopentane which boils at 9 °C and is a liquid in an ice bath.
The first feature assures that each compound gives a single sharp resonance signal. The second allows the pure (neat) substance to be poured into a sample tube and examined in a NMR spectrometer. In order to take the NMR spectra of a solid, it is usually necessary to dissolve it in a suitable solvent. Early studies used carbon tetrachloride for this purpose, since it has no hydrogen that could introduce an interfering signal. Unfortunately, CCl4 is a poor solvent for many polar compounds and is also toxic. Deuterium labeled compounds, such as deuterium oxide (D2O), chloroform-d (DCCl3), benzene-d6 (C6D6), acetone-d6 (CD3COCD3) and DMSO-d6 (CD3SOCD3) are now widely used as NMR solvents. Since the deuterium isotope of hydrogen has a different magnetic moment and spin, it is invisible in a spectrometer tuned to protons.
For the properties of some common NMR solvents Click Here.
From the previous discussion and examples we may deduce that one factor contributing to chemical shift differences in proton resonance is the inductive effect. If the electron density about a proton nucleus is relatively high, the induced field due to electron motions will be stronger than if the electron density is relatively low. The shielding effect in such high electron density cases will therefore be larger, and a higher external field (Bo) will be needed for the rf energy to excite the nuclear spin. Since silicon is less electronegative than carbon, the electron density about the methyl hydrogens in tetramethylsilane is expected to be greater than the electron density about the methyl hydrogens in neopentane (2,2-dimethylpropane), and the characteristic resonance signal from the silane derivative does indeed lie at a higher magnetic field. Such nuclei are said to be shielded. Elements that are more electronegative than carbon should exert an opposite effect (reduce the electron density); and, as the data in the following tables show, methyl groups bonded to such elements display lower field signals (they are deshielded). The deshielding effect of electron withdrawing groups is roughly proportional to their electronegativity, as shown by the left table. Furthermore, if more than one such group is present, the deshielding is additive (table on the right), and proton resonance is shifted even further downfield.
Proton Chemical Shifts of Methyl Derivatives
|
Proton Chemical Shifts (ppm)
|
|---|
The general distribution of proton chemical shifts associated with different functional groups is summarized in the following chart. Bear in mind that these ranges are approximate, and may not encompass all compounds of a given class. Note also that the ranges specified for OH and NH protons (colored orange) are wider than those for most CH protons. This is due to hydrogen bonding variations at different sample concentrations.
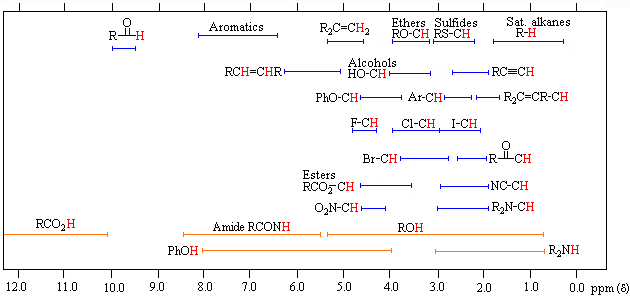
Proton Chemical Shift Ranges* |
||
|---|---|---|
|
Low Field |
|
High Field |
|
* For samples in CDCl3 solution. The δ scale is relative to TMS at δ = 0. |
||
To make use of a calculator that predicts aliphatic proton chemical shifts Click Here. This application was developed at Colby College.
Signal Strength
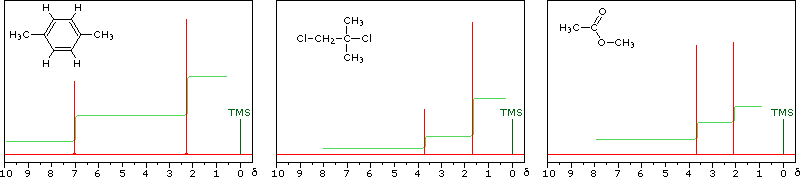
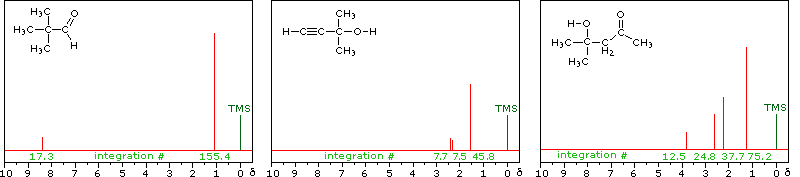
The magnitude or intensity of NMR resonance signals is displayed along the vertical axis of a spectrum, and is proportional to the molar concentration of the sample. Thus, a small or dilute sample will give a weak signal, and doubling or tripling the sample concentration increases the signal strength proportionally. If we take the NMR spectrum of equal molar amounts of benzene and cyclohexane in carbon tetrachloride solution, the resonance signal from cyclohexane will be twice as intense as that from benzene because cyclohexane has twice as many hydrogens per molecule. This is an important relationship when samples incorporating two or more different sets of hydrogen atoms are examined, since it allows the ratio of hydrogen atoms in each distinct set to be determined. To this end it is necessary to measure the relative strength as well as the chemical shift of the resonance signals that comprise an NMR spectrum. Two common methods of displaying the integrated intensities associated with a spectrum are illustrated by the following examples. In the three spectra in the top row, a horizontal integrator trace (light green) rises as it crosses each signal by a distance proportional to the signal strength. Alternatively, an arbitrary number, selected by the instrument's computer to reflect the signal strength, is printed below each resonance peak, as shown in the three spectra in the lower row. From the relative intensities shown here, together with the previously noted chemical shift correlations, the reader should be able to assign the signals in these spectra to the set of hydrogens that generates each. If you click on one of the spectrum signals (colored red) or on hydrogen atom(s) in the structural formulas the spectrum will be enlarged and the relationship will be colored blue. Hint: When evaluating relative signal strengths, it is useful to set the smallest integration to unity and convert the other values proportionally.