NS14. Stereochem in Elimination
- Page ID
- 4304
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)NS14. Stereochemistry in Elimination
Sometimes, elimination reactions may lead to multiple stereoisomers; that is, they could lead to either the cis or the trans isomer, or in more complicated structures, either the Z or the E isomer.
Of course, if there were some inherent stability difference between these isomers, that could be a factor that plays a role in influencing the outcome. Elimination reactions aren't generally reversible, so products are not directly determined by alkene isomer stabilities. Nevertheless, sometimes the barrier leading to a more stable product is a little lower than the barrier leading to a less stable product.
We do know that in simple cis vs. trans cases, the trans isomer is generally lower in energy because of fewer steric interactions between the substituents on the double bond. In the absence of other information, we could take that as a starting point. Let's see whether elimination reactions generally lead to trans isomers.
It turns out that sometimes this is true: eliminations often lead to the more stable product. Sometimes it isn't true, though. The answer depends on the mechanism.
- E1 eliminations generally lead to the more stable stereochemistry.
- E2 eliminations may or may not lead to the more stable stereochemistry.
Instead, in an E2 reaction, stereochemistry of the double bond -- that is, whether the E or Z isomer results -- is dictated by the stereochemistry of the starting material, if it is diastereomeric. In other words, if the carbon with the hydrogen and the carbon with the halogen are both chiral, then one diastereomer will lead to one product, and the other diastereomer will lead to the other product.
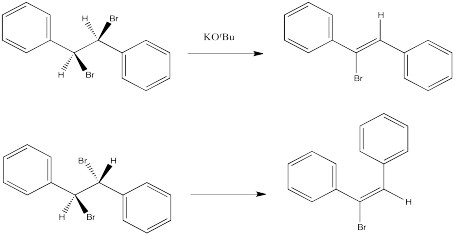
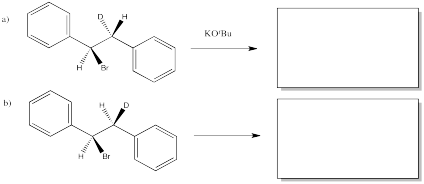
The following reactions of potassium ethoxide with dibromostilbene (1,2-dibromo-1,2-diphenylethane) both occurred via an E2 mechanism. Two different diastereomers were used. Two different stereoisomers (E vs. Z) resulted.
Problem NS14.1.
Provide the stereochemical configurations of the following compounds from the above reactions:
- 1,2-dibromo-1,2-diphenylethane (upper example)
- 1-bromo-1,2-diphenylethene (upper example)
- 1,2-dibromo-1,2-diphenylethane (lower example)
- 1-bromo-1,2-diphenylethene (lower example)
In E2 eliminations, the spatial relationship between the proton and leaving group determines the product stereochemistry. That's because pi bond formation happens at the same time that the halide leaves and at the same time that the base removes the proton. All of these events have to be coordinated together. The central, tricky event is the pi bond formation. The leaving group can leave in any direction, and the base can approach from many directions, but unless the pi bond is ready to form, nothing else happens.
Let's slow the reaction down and imagine it takes place in slightly different stages.
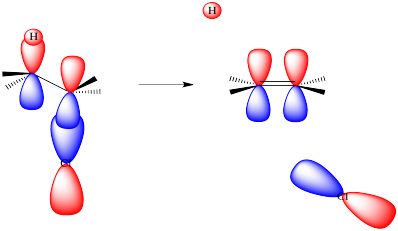
As the leaving group leaves, it takes its electrons with it. It begins to leave a positive charge behind. That positive charge will be centered on the carbon from which the halide is departing. That carbocation, if it fully formed, would have only three neighbours to bond with. It would be trigonal planar. It would have an unoccupied, non-bonding p orbital.
As the base takes the proton, the hydrogen leaves behind the electrons from the C-H bond that held it in place. These electrons stay behind on the carbon atom. They are left in a non-bonding carbon valence orbital, a p orbital or something quite like it.
Now we have a filled p orbital next to an empty p orbital. They overlap to form a pi bond.
Of course, in an E2 reaction, things don't happen in stages. Everything happens at once. That means that, as the base removes the proton, the pi bond must already start forming. Because a pi bond requires parallel alignment of two p orbitals, and the p orbitals are forming from the C-H and C-LGp bonds, then those bonds must line up in order for the elimination to occur.
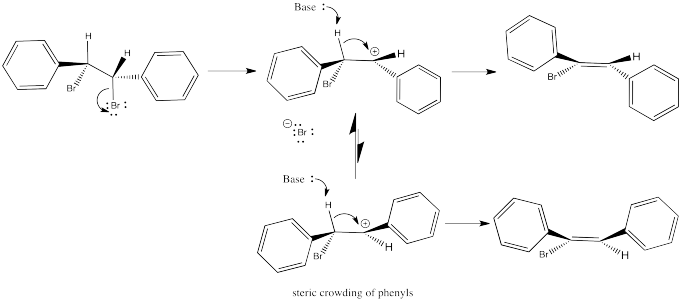
So let's look again at that dibromostilbene example.
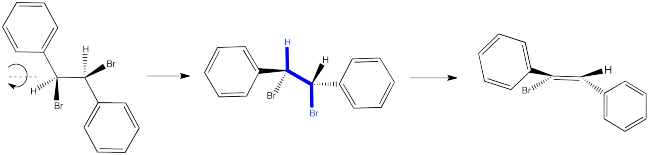
In the first case, we need to spin the molecule so that we can see how the H on one carbon and the Br on the other are aligned and ready to eliminate via an E2 reaction. The substituents coming towards us in the reactant will still be coming towards us in the product. The substituents pointing away from us in the reactant will still be pointing away from us in the product.
So the relationships between the substituents on the nascent double bond are determined by their relationship once the reactant is aligned for the E2 reaction.
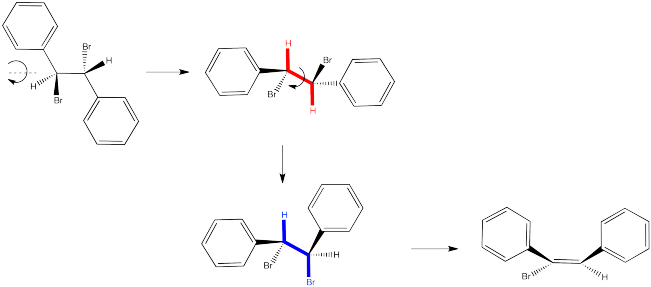
In the second case, we can spin the molecule but quickly realize the C-H and C-Br bonds are not lined up in this conformer. We need a bond rotation. Once we have made a conformational change, the C-H and C-Br bonds line up. It doesn't matter if this conformer is not favoured; if there is going to be any E2 reaction at all, this is the conformer it will have to go through.
Again, the relationships between on the new double bond are determined by their relationship once the reactant is aligned for the E2 reaction.
Problem NS14.2.
Sometimes it is easier to see the relationships between substituents by using a Newman projection. Draw Newman projections showing how the two isomers above proceed to different products in an E2 reaction.
Problem NS14.3.
Predict the product of each of the following E2 reactions. Note that the compounds differ in the incorporation of a 2H isotope (deuterium, or D) in place of a regular 1H isotope (protium, or H).
Problem NS14.4.
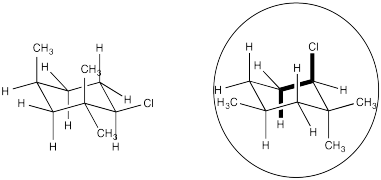
Conformational analysis of cyclohexanes requires the use of diamond lattice projections ("chairs"). Show why elimination can't proceed through the E2 mechanism in the following compound.
Problem NS14.5.
Predict the E2 elimination products from the following compounds.
In contrast to E2 reactions, E1 reactions do not occur in one step. That means there is time for reorganization in the intermediate. Once the leaving group leaves, the cation can sort itself into the most stable conformer. When the proton is taken, generally the most stable stereoisomer results because it comes from the most stable conformer of the cation. Any steric interactions in the alkene would also have occurred in the cation, so this interaction would have been sorted out at that point.
Thus, in the case of the dibromostilbenes examined before, E1 elimination would result in the same product in either case.
- E1 reactions can, in principle, lead to either stereochemistry of alkene.
- Free rotation around bonds in the carbocation intermediate allows the cation to adopt either conformer prior to elimination.
- However, steric interactions will lead to a preponderance of one conformer.
- The more stable conformer will lead to the more stable alkene.