Optical Isomerism in Organic Molecules
- Page ID
- 3652
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Optical isomerism is a form of stereoisomerism. This page explains what stereoisomers are and how you recognize the possibility of optical isomers in a molecule.
What are stereoisomers?
Isomers are molecules that have the same molecular formula, but have a different arrangement of the atoms in space. That excludes any different arrangements which are simply due to the molecule rotating as a whole, or rotating about particular bonds. Where the atoms making up the various isomers are joined up in a different order, this is known as structural isomerism. Structural isomerism is not a form of stereoisomerism, which involve the atoms of the complex bonded in the same order, but in different spatial arrangements. Optical isomerism is one form of stereoisomerism; geometric isomers are a second type.
Optical isomerism
Optical isomers are named like this because of their effect on plane polarized light. Simple substances which show optical isomerism exist as two isomers known as enantiomers.
- A solution of one enantiomer rotates the plane of polarisation in a clockwise direction. This enantiomer is known as the (+) form.
- For example, one of the optical isomers (enantiomers) of the amino acid alanine is known as (+)alanine.
- A solution of the other enantiomer rotates the plane of polarisation in an anti-clockwise direction. This enantiomer is known as the (-) form. So the other enantiomer of alanine is known as or (-)alanine.
- If the solutions are equally concentrated the amount of rotation caused by the two isomers is exactly the same - but in opposite directions.
- When optically active substances are made in the lab, they often occur as a 50/50 mixture of the two enantiomers. This is known as a racemic mixture or racemate. It has no effect on plane polarised light.
Origin of Optical Isomers
The examples of organic optical isomers contain a carbon atom joined to four different groups. These two models each have the same groups joined to the central carbon atom, but still manage to be different:
Obviously as they are drawn, the orange and blue groups are not aligned the same way. Could you get them to align by rotating one of the molecules? The next diagram shows what happens if you rotate molecule B.
They still are not the same - and there is no way that you can rotate them so that they look exactly the same. These are isomers of each other. They are described as being non-superimposable in the sense that (if you imagine molecule B being turned into a ghostly version of itself) you couldn't slide one molecule exactly over the other one. Something would always be pointing in the wrong direction.
What happens if two of the groups attached to the central carbon atom are the same? The next diagram shows this possibility.
The two models are aligned exactly as before, but the orange group has been replaced by another pink one. Rotating molecule B this time shows that it is exactly the same as molecule A. You only get optical isomers if all four groups attached to the central carbon are different.
Chiral and achiral molecules
The essential difference between the two examples we've looked at lies in the symmetry of the molecules. If there are two groups the same attached to the central carbon atom, the molecule has a plane of symmetry. If you imagine slicing through the molecule, the left-hand side is an exact reflection of the right-hand side.
Where there are four groups attached, there is no symmetry anywhere in the molecule
A molecule which has no plane of symmetry is described as chiral. The carbon atom with the four different groups attached which causes this lack of symmetry is described as a chiral center or as an asymmetric carbon atom. The molecule on the left above (with a plane of symmetry) is described as achiral. Only chiral molecules have optical isomers.
The relationship between the enantiomers
One of the enantiomers is simply a non-superimposable mirror image of the other one. In other words, if one isomer looked in a mirror, what it would see is the other one. The two isomers (the original one and its mirror image) have a different spatial arrangement, and so cannot be superimposed on each other.
If an achiral molecule (one with a plane of symmetry) looked in a mirror, you would always find that by rotating the image in space, you could make the two look identical. It would be possible to superimpose the original molecule and its mirror image.
The asymmetric carbon atom in a compound (the one with four different groups attached) is often shown by a star.
It's extremely important to draw the isomers correctly. Draw one of them using standard bond notation to show the 3-dimensional arrangement around the asymmetric carbon atom. Then draw the mirror to show the examiner that you know what you are doing, and then the mirror image.
Notice that you don't literally draw the mirror images of all the letters and numbers! It is, however, quite useful to reverse large groups - look, for example, at the ethyl group at the top of the diagram. It doesn't matter in the least in what order you draw the four groups around the central carbon. As long as your mirror image is drawn accurately, you will automatically have drawn the two isomers.
So which of these two isomers is (+)butan-2-ol and which is (-)butan-2-ol? There is no simple way of telling that. For A'level purposes, you can just ignore that problem - all you need to be able to do is to draw the two isomers correctly.
Once again the chiral center is shown by a star.
The two enantiomers are:
It is important this time to draw the COOH group backwards in the mirror image. If you don't there is a good chance of you joining it on to the central carbon wrongly.
If you draw it like this in an exam, you will not get the mark for that isomer even if you have drawn everything else perfectly.
This is typical of naturally-occurring amino acids. Structurally, it is just like the last example, except that the -OH group is replaced by -NH2
The two enantiomers are:
Only one of these isomers occurs naturally: the (+) form. You cannot tell just by looking at the structures which this is.
It has, however, been possible to work out which of these structures is which. Naturally occurring alanine is the right-hand structure, and the way the groups are arranged around the central carbon atom is known as an L- configuration. Notice the use of the capital L. The other configuration is known as D-.
So you may well find alanine described as L-(+)alanine. That means that it has this particular structure and rotates the plane of polarization clockwise.
Even if you know that a different compound has an arrangement of groups similar to alanine, you still cannot say which way it will rotate the plane of polarization. The other amino acids, for example, have the same arrangement of groups as alanine does (all that changes is the CH3 group), but some are (+) forms and others are (-) forms.
It's quite common for natural systems to only work with one of the enantiomers of an optically active substance. It is not too difficult to see why that might be. Because the molecules have different spatial arrangements of their various groups, only one of them is likely to fit properly into the active sites on the enzymes they work with.
In the lab, it is quite common to produce equal amounts of both forms of a compound when it is synthesized. This happens just by chance, and you tend to get racemic mixtures.
Identifying Chiral Centers
A skeletal formula is the most stripped-down formula possible. Look at the structural formula and skeletal formula for butan-2-ol.
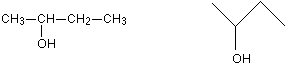
Notice that in the skeletal formula all of the carbon atoms have been left out, as well as all of the hydrogen atoms attached to carbons. In a skeletal diagram of this sort:
- there is a carbon atom at each junction between bonds in a chain and at the end of each bond (unless there is something else there already - like the -OH group in the example);
- there are enough hydrogen atoms attached to each carbon to make the total number of bonds on that carbon up to 4.
We have already discussed the butan-2-ol case further up the page, and you know that it has optical isomers. The second carbon atom (the one with the -OH attached) has four different groups around it, and so is a chiral center.
Is this obvious from the skeletal formula? Well, it is, provided you remember that each carbon atom has to have 4 bonds going away from it. Since the second carbon here only seems to have 3, there must also be a hydrogen attached to that carbon. So it has a hydrogen, an -OH group, and two different hydrocarbon groups (methyl and ethyl).
Four different groups around a carbon atom means that it is a chiral center.
The diagrams show an uncluttered skeletal formula, and a repeat of it with two of the carbons labeled.

Look first at the carbon atom labeled 2. Is this a chiral center? No, it is not. Two bonds (one vertical and one to the left) are both attached to methyl groups. In addition, of course, there is a hydrogen atom and the more complicated hydrocarbon group to the right. It doesn't have 4 different groups attached, and so is not a chiral center.
What about the number 3 carbon atom? This has a methyl group below it, an ethyl group to the right, and a more complicated hydrocarbon group to the left. Plus, of course, a hydrogen atom to make up the 4 bonds that have to be formed by the carbon. That means that it is attached to 4 different things, and so is a chiral center.
Introducing Rings
We will start with a fairly simple ring compound:
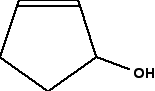
When you are looking at rings like this, as far as optical isomerism is concerned, you don't need to look at any carbon in a double bond. You also don't need to look at any junction which only has two bonds going away from it. In that case, there must be 2 hydrogens attached, and so there cannot possibly be 4 different groups attached.
In this case, that means that you only need to look at the carbon with the -OH group attached. It has an -OH group, a hydrogen (to make up the total number of bonds to four), and links to two carbon atoms. How does the fact that these carbon atoms are part of a ring affect things?
You just need to trace back around the ring from both sides of the carbon you are looking at. Is the arrangement in both directions exactly the same? In this case, it is not. Going in one direction, you come immediately to a carbon with a double bond. In the other direction, you meet two singly bonded carbon atoms, and then one with a double bond. That means that you haven't got two identical hydrocarbon groups attached to the carbon you are interested in, and so it has 4 different groups in total around it. It is asymmetric - a chiral center.
What about this near-relative of the last molecule?
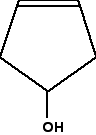
In this case, everything is as before, except that if you trace around the ring clockwise and counter-clockwise from the carbon at the bottom of the ring, there is an identical pattern in both directions. You can think of the bottom carbon being attached to a hydrogen, an -OH group, and two identical hydrocarbon groups. It therefore is not a chiral center.
The other thing which is very noticeable about this molecule is that there is a plane of symmetry through the carbon atom we are interested in. If you chopped it in half through this carbon, one side of the molecule would be an exact reflection of the other. In the first ring molecule above, that is not the case.
If you can see a plane of symmetry through the carbon atom it will not be a chiral center. If there is not a plane of symmetry, it will be a chiral center.
The skeletal diagram shows the structure of cholesterol. Some of the carbon atoms have been numbered for discussion purposes below. These are not part of the normal system for numbering the carbon atoms in cholesterol.
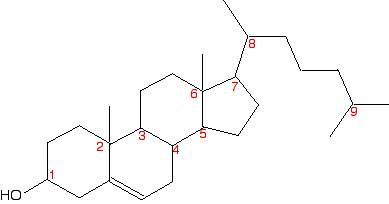
Before you read on, look carefully at each of the numbered carbon atoms, and decide which of them are chiral centers. The other carbon atoms in the structure cannot be chiral centers, because they are either parts of double bonds, or are joined to either two or three hydrogen atoms.
So . . . how many chiral centers did you find? In fact, there are 8 chiral centers out of the total of 9 carbons marked. If you didn't find all eight, go back and have another look before you read any further. It might help to sketch the structure on a piece of paper and draw in any missing hydrogens attached to the numbered carbons, and write in the methyl groups at the end of the branches as well.
This is done for you below, but it would be a lot better if you did it yourself and then checked your sketch afterwards .
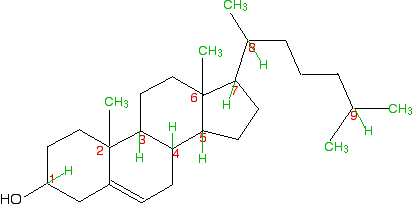
Starting with the easy one - it is obvious that carbon 9 has two methyl groups attached. It doesn't have 4 different groups, and so cannot be chiral. If you take a general look at the rest, it is fairly clear that none of them has a plane of symmetry through the numbered carbons. Therefore they are all likely to be chiral centers. But it's worth checking to see what is attached to each of them.
- Carbon 1 has a hydrogen, an -OH and two different hydrocarbon chains (actually bits of rings) attached. Check clockwise and anticlockwise, and you will see that the arrangement is not identical in each direction. Four different groups means a chiral center.
- Carbon 2 has a methyl and three other different hydrocarbon groups. If you check along all three bits of rings , they are all different - another chiral center. This is also true of carbon 6.
- Carbons 3, 4, 5 and 7 are all basically the same. Each is attached to a hydrogen and three different bits of rings. All of these are chiral centers.
- Finally, carbon 8 has a hydrogen, a methyl group, and two different hydrocarbon groups attached. Again, this is a chiral center.
This all looks difficult at first glance, but it is not. You do, however, have to take a great deal of care in working through it - it is amazingly easy to miss one out.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


