Hückel's Rule
- Page ID
- 927
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In 1931, German chemist and physicist Erich Hückel proposed a rule to determine if a planar ring molecule would have aromatic properties. This rule states that if a cyclic, planar molecule has \(4n+2\; \pi\) electrons, it is aromatic. This rule would come to be known as Hückel's Rule.
Four Criteria for Aromaticity
When deciding if a compound is aromatic, go through the following checklist. If the compound does not meet all the following criteria, it is likely not aromatic.
- The molecule is cyclic (a ring of atoms)
- The molecule is planar (all atoms in the molecule lie in the same plane)
- The molecule is fully conjugated (p orbitals at every atom in the ring)
- The molecule has \(4n+2\; \pi\) electrons (n=0 or any positive integer)
Why 4n+2 π Electrons?
According to Hückel's Molecular Orbital Theory, a compound is particularly stable if all of its bonding molecular orbitals are filled with paired electrons. This is true of aromatic compounds, meaning they are quite stable. With aromatic compounds, 2 electrons fill the lowest energy molecular orbital, and 4 electrons fill each subsequent energy level (the number of subsequent energy levels is denoted by \(n\)), leaving all bonding orbitals filled and no anti-bonding orbitals occupied. This gives a total of \(4n+2 \; \pi\) electrons. You can see how this works with the molecular orbital diagram for the aromatic compound, benzene, below.
.jpg?revision=1&size=bestfit&width=317&height=254)
Figure 1: Molecular Orbitals levels of Benzene
Benzene has 6 \(\pi\) electrons. Its first 2 \(\pi\) electrons fill the lowest energy orbital, and it has 4 \(\pi\) electrons remaining. These 4 fill in the orbitals of the succeeding energy level. Notice how all of its bonding orbitals are filled, but none of the anti-bonding orbitals have any electrons.
Confirm that benzene is aromatic.
Solution
To apply the 4n+2 rule, first count the number of π electrons in the molecule. Then, set this number equal to 4n+2 and solve for n. If is 0 or any positive integer (1, 2, 3,...), the rule has been met. For example, benzene has six π electrons:
4n + 2 = 6
4n = 4
n = 1
For benzene, we find that n=1, which is a positive integer, so the rule is met.
How Can You Tell Which Electrons are π Electrons?
Perhaps the toughest part of Hückel's Rule is figuring out which electrons in the compound are actually π electrons. Once this is figured out, the rule is quite straightforward. π electrons lie in p orbitals. Sp2 hybridized atoms have 1 p orbital each. So if every molecule in the cyclic compound is sp2 hybridized, this means the molecule is fully conjugated (has 1 p orbital at each atom), and the electrons in these p orbitals are the π electrons. A simple way to know if an atom is sp2 hybridized is to see if it has 3 attached atoms and no lone pairs of electrons. This video provides a very nice tutorial on how to determine an atom's hybridization. In a cyclic hydrocarbon compound with alternating single and double bonds, each carbon is attached to 1 hydrogen and 2 other carbons. Therefore, each carbon is sp2 hybridized and has a p orbital. Let's look at our previous example, benzene:
.jpg?revision=1)
Each double bond (π bond) always contributes 2 π electrons. Benzene has 3 double bonds, so it has 6 π electrons.
Aromatic Ions
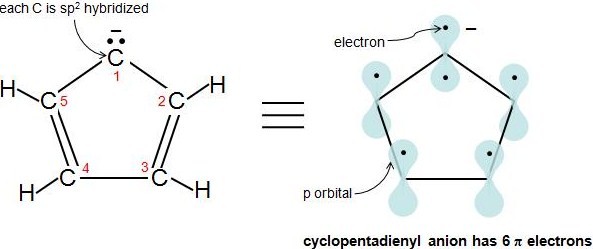
Hückel's Rule also applies to ions. As long as a compound has 4n+2 π electrons, it does not matter if the molecule is neutral or has a charge. For example, cyclopentadienyl anion is an aromatic ion. How do we know that it is fully conjugated? That is, how do we know that each atom in this molecule has 1 p orbital? Let's look at the following figure. Carbons 2-5 are sp2 hybridized because they have 3 attached atoms and have no lone electron pairs. What about carbon 1? Another simple rule to determine if an atom is sp2 hybridized is if an atom has 1 or more lone pairs and is attached to an sp2 hybridized atom, then that atom is sp2 hybridized also. This video explains the rule very clearly. Therefore, carbon 1 has a p orbital. Cyclopentadienyl anion has 6 π electrons and fulfills the 4n+2 rule.
.jpg?revision=1)
Heterocyclic Aromatic Compounds
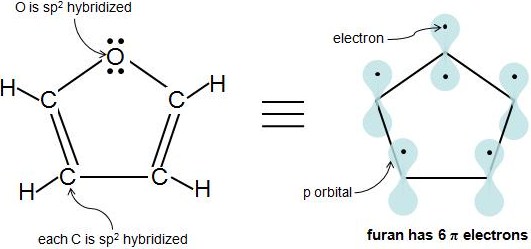
So far, you have encountered many carbon homocyclic rings, but compounds with elements other than carbon in the ring can also be aromatic, as long as they fulfill the criteria for aromaticity. These molecules are called heterocyclic compounds because they contain 1 or more different atoms other than carbon in the ring. A common example is furan, which contains an oxygen atom. We know that all carbons in furan are sp2 hybridized. But is the oxygen atom sp2 hybridized? The oxygen has at least 1 lone electron pair and is attached to an sp2 hybridized atom, so it is sp2 hybridized as well. Notice how oxygen has 2 lone pairs of electrons. How many of those electrons are π electrons? An sp2 hybridized atom only has 1 p orbital, which can only hold 2 electrons, so we know that 1 electron pair is in the p orbital, while the other pair is in an sp2 orbital. So, only 1 of oxygen's 2 lone electron pairs are π electrons. Furan has 6 π electrons and fulfills the 4n+2 rule.
.jpg?revision=1)
Problems
Using the criteria for aromaticity, determine if the following molecules are aromatic:
.jpg?revision=1)
Answers
- Aromatic - only 1 of S's lone pairs counts as π electrons, so there are 6 π electrons, n=1
- Not aromatic - not fully conjugated, top C is sp3 hybridized
- Not aromatic - top C is sp2 hybridized, but there are 4 π electrons, n=1/2
- Aromatic - N is using its 1 p orbital for the electrons in the double bond, so its lone pair of electrons are not π electrons, there are 6 π electrons, n=1
- Aromatic - there are 6 π electrons, n=1
- Not aromatic - all atoms are sp2 hybridized, but only 1 of S's lone pairs counts as π electrons, so there 8 π electrons, n=1.5
- Not aromatic - there are 4 π electrons, n=1/2
- Aromatic - only 1 of N's lone pairs counts as π electrons, so there are 6 π electrons, n=1
- Not aromatic - not fully conjugated, top C is sp3 hybridized
- Aromatic - O is using its 1 p orbital for the elections in the double bond, so its lone pair of electrons are not π electrons, there are 6 π electrons, n=1
References
- Vollhardt, Peter, and Neil E. Schore. Organic Chemistry: Structure and Function. 5th ed. New York: W. H. Freeman & Company, 2007.
- Berson, Jerome. Chemical Creativity: Ideas from the Work of Woodward, Hückel, Meerwein, and Others. New York: Wiley-VCH, 1999.
- Badger, G.M. Aromatic Character and Aromaticity. London, England: Cambridge University Press, 1969.
- Lewis, David and David Peters. Facts and Theories of Aromaticity. London, England: Macmillan Press, 1975.