Rings: cis/trans and axial/equatorial relationships
- Page ID
- 854
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The purpose of this page is to help organic chem students show how substituent groups are located on ring structures. We focus here on six-membered rings (6-rings); these are among the most common rings in organic chem (and biochem), and they suffice to raise the main issues. We will look at how to show cis and trans relationships in simple hexagon structural formulas, and we will look at structures showing the common "chair" conformation, focusing on axial vs equatorial orientations. We will also discuss the relationship between cis/trans and axial/equatorial.
Introduction
The basic approach here is to look at a series of compounds, of generally increasing complexity. They are chosen to illustrate one new feature at a time of how to draw the structures and how to see cis/trans and axial/equatorial features.
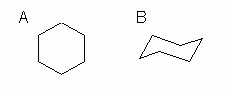
Cyclohexane
Figure 1: This basic 6-ring cycloalkane, without any special substituents (i.e., other than hydrogen), is easily shown by either of the formulas in Fig 1.
Both structures clearly imply six C in a ring, with two H at each position. Fig 1A is a simple structural formula, condensed. We say it is "condensed" because not all features are shown explicitly. In fact, in this case, not much at all is shown explicitly: the C atoms are understood (at each vertex), the H atoms are understood (enough at each C to give C its normal four bonds), and the C-H bonds are understood. About all that is explicit is the basic carbon skeleton (C-C bonds), showing that there are six C atoms in a ring. Fig 1B is very much like Fig 1A, but it adds one new feature: Fig 1B attempts to show the conformation of the molecule. In this case, we understand that cyclohexane and its simple derivatives tend to spend most of their time near this "chair" conformation. Glossary entry: Conformation.
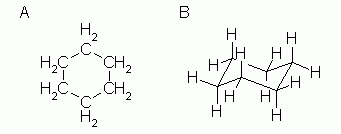
Figure 2: If we want to show the hydrogen atoms explicitly, we can do so with structural formulas such as in Fig 2.
There is little room for confusion here, since all six C atoms are equivalent, as are all 12 H atoms.
For notes on how to draw chairs, see the section E.2. Note: How to draw chairs.
Chlorocyclohexane
This is an example of the next level of complexity, a mono-substituted cycloalkane. See Fig 3. |
Figure 3 |
 |
So what is new here? Not much, with the hexagon formula, Fig 3A. That type of formula shows the basic "connectivity" of the atoms -- who is connected to whom. This chemical has one Cl on the ring, and it does not matter where we show it. There is now only one H on that C, but since we are not showing H explicitly here, that is not an issue in drawing the structure. (It is an issue when you look at it and want to count H.)
With the chair formula (Fig 3B), which shows information not only about connectivity but also about conformation, there is important new information here. In a chair, there are two "types" of substituents: those pointing up or down, and called axial, and those pointing "outward", and called equatorial. I have shown the chlorine atom in an equatorial position. Why? Two reasons: it is what we would predict, and it is what is found. Why do we predict that the Cl is equatorial? Because it is bigger than H, and there is more room in the equatorial positions.
Helpful Hints...
If possible, examine a physical model of cyclohexane and chlorocyclohexane, so that you can see the axial and equatorial positions. Common ball and stick models are fine for this. It should be easy to see that the three axial H on one side can get very near each other.
If you do not have access to physical models, examining computer models can also be useful. See my RasMol page for a program and source of structures for this.
When putting substituents on chair structures, I encourage you to use the four corner positions of the chair as much as possible. It is easier to see the axial and equatorial relationship at the corners.
In Fig 3B I have shown the H atom that is on the same carbon as the Cl atom. This is perhaps not necessary, since the correct number of H atoms is understood, by counting bonds on C. But showing the H explicitly at key C atoms helps to make the structure clearer. This may be particularly important with hand-drawn structures. I often see structures where I am not sure whether a particular atom is shown axial or equatorial. But if both atoms at the position (the H as well as the Cl) are shown, then hopefully it becomes clearer which is which. I also encourage students who are not sure of their art work to annotate their drawing. Say what you mean. That allows me to distinguish whether you are unsure which direction things point or simply unsure how to draw them.)
Again, a reminder... For notes on how to draw chairs (by hand or using a drawing program), see the section E.2. Note: How to draw chairs.
D. Dichlorocyclohexanes: an introduction
The next level of complexity is a di-substituted cycloalkane, "dichlorocyclohexane". The first question we must ask is which C the two chlorine substituents are on. For now, I want to discuss 1,3- dichlorocyclohexane. This introduces another issue: are the two Cl on the same side of the ring, or on opposite sides? We call these "cis" (same side) and "trans" (opposite sides). We focus on one of these, cis-1,3-dichlorocyclohexane. And for now, we will just look at hexagon structural formulas, leaving the question of conformation for later. Let's go through this one step at a time.
1,3-Dichlorocyclohexane
Our first attempt to draw 1,3-dichlorocyclohexane might look something like Fig 4. |
Figure 4 |
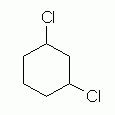 |
The structure in Fig 4 is indeed a dichlorocyclohexane. It is even a 1,3-dichlorocyclohexane. However, this structure provides no information about the orientation of the two Cl atoms relative to the plane of the ring. To show a specific isomer -- cis or trans -- we must somehow show how the two Cl atoms are oriented relative to the plane of the ring.
cis-1,3-Dichlorocyclohexane
Fig 5 shows two common ways to show how the substituents are oriented relative to the plane of the ring. The compound shown here is cis-1,3-dichlorocyclohexane. |
Figure 5 |
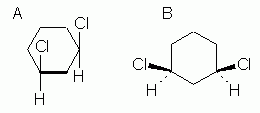 |
The basic idea in both of these is that we can imagine the ring to be planar, and then show the groups above or below the plane of the ring. How we show this is different in the two parts of Fig 5. In Fig 5A, we look at the ring "edge-on". The thick line for the bottom bond is intended to convey the edge-on view (or side view); this is sometimes omitted, especially with hand-drawn structures, but be careful then that the meaning is clear. Once we understand that we are now looking at the ring edge-on, it is clear that the two Cl atoms are both above the ring, hence cis. In Fig 5B, we view the ring "face-on" (or top view), and use special bond symbols -- "stereo bonds" -- to convey up and down: the heavy wedge -- an "up wedge" -- points upward, toward you, and the dashed bond -- a "down bond" -- points downward, away from you. Again, both Cl are "up", hence cis.
Notes...
For some notes on how to draw the stereo bonds, see the section E.1. Note: How to draw stereo bonds ("up" and "down" bonds).
In discussing Fig 5, I started by saying that we imagine the ring to be planar. Emphasize that cycloalkane rings are not really planar (except for cyclopropane rings). As so often, the structural formula represents the general layout of the atoms, but not the actual molecular geometry.
Those with the Ouellette book can see examples of these two ways of showing up/down on p 81 (top) and p 80 (middle). Most organic chemistry books will show you this.
The conformation of cis-1,3-dichlorocyclohexane
Fig 6, at the right, is one way to show this. Fig 6 shows features of the compound that we have already noted -- plus one more. Let's go through these features, emphasizing what is new. |
Figure 6 |
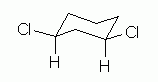 |
The structure shows cis-1,3-dichlorocyclohexane: a 6-ring; 2 Cl atoms, at positions 1 and 3; and cis, with both Cl on the same side of -- above -- the H that is on the same C.
I showed the 2 Cl atoms at corner positions, and I showed the H at the key positions explicitly. These points follow from some of the Helpful Hints discussed earlier. It is not required that you do these things, but they can make things easier for you -- and for anyone reading your structures.
Now, what is new here? The conformation. We start with the notion that the conformation of cyclohexane derivatives is based on the "chair". At each position, one substituent is axial (loosely, perpendicular to the ring), and one is equatorial (loosely, in the plane of the ring). There is more room in the equatorial positions (not easily seen with these simple drawings, but ordinary ball and stick models do help with this point). Thus we try to put the larger substituents in the equatorial positions. In this case, we put the Cl equatorial and the H axial at each position 1 and position 3.
We are now done with this compound, cis-1,3-dichlorocyclohexane. However, we have missed one very important concern -- because it is not an issue in this case. So let's look at another compound.
cis-1,2-Dichlorocyclohexane
cis-1,2-Dichlorocyclohexane is like the previous compound, except that the two chloro groups are now at 1,2, rather than at 1,3. Fig 7 shows a simple structural formula for 1,2-dichlorocyclohexane, without orientation. This is analogous to Fig 4 above for the 1,3 isomer. |
Figure 7 |
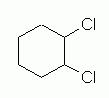 |
Figure 8 |
Fig 8 shows two ways to show the cis orientation in cis-1,2-dichlorocyclohexane. This Fig is analogous to Fig 5 above for the 1,3 isomer. |
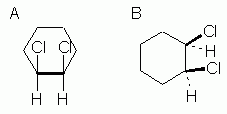 |
Figures 7 and 8 above introduce no new ideas or complications. These two figures should be straightforward.
So, what is the preferred conformation of cis-1,2-dichlorocyclohexane? This requires careful consideration; an important lesson from this exercise is to realize that we cannot propose a good conformation based simply on what we have learned so far.
The two guidelines we have so far for conformation of 6-rings are:
- The carbon ring is in a chair.
- Larger substituents are in equatorial positions.
Let's explore the difficulty here by looking at some things people might naively draw.
| Figure 9 | Fig 9 shows an attempt to draw a chair conformation of cis-1,2-dichlorocyclohexane. It satisfies both of the guidelines listed above. But it is wrong. |
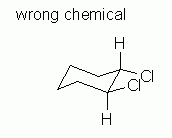 |
Why is Fig 9 wrong? It is the wrong chemical. The structure shown in Fig 9 is trans, not cis. Look carefully at the 1 and 2 positions. At one of them, the H is above the Cl; at the other, the Cl is above the H. Trans. Wrong chemical. The structure shown in Fig 9 is not the requested chemical.
| Figure 10 | Fig 10 attempts to fix the problem with Fig 9. But it is also wrong. |
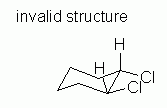 |
Why is Fig 10 wrong? After all, it seems to address the criteria presented. It contains both of the larger atoms (Cl) equatorial, and they are cis as desired. However, in Fig 10, the two axial groups on carbons # 1 and 2 (the two H that are shown) are both pointing up. This is impossible. In a valid chair, the axial groups alternate up/down as one goes around the ring; see Figure 2B, above. This follows from the tetrahedral bonding of C. Adjacent axial groups, as relevant here, must point in opposite directions; that condition is violated here. That is, Fig 10 is not a valid chair.
Those who find the above point new or surprising should check their textbook. If possible, look at models of cyclohexane and simple derivatives such as the one here. Figure 2B, above, is correct. In my experience, many students have not yet noticed this feature of chair conformations.
If you think you have an alternative that is better (or even satisfactory), please show it to me. I suspect it will turn out to be equivalent to Fig 9 or Fig 10, above. But if you think it is good, let's discuss it.
So now what? We have a contradiction. And that really is the most important point here. It is important to realize that we cannot draw a conformation for cis-1,2-dichlorocyclohexane which easily fits the criteria we have used so far: a chair, with large groups equatorial. So what do we do? Clearly, the conformation of this compound must, in some way, involve more issues than what we have considered so far.
Instructors and books will vary in how much further explanation they want to give on this matter. Therefore, how you proceed from here must take into account the preferences in your course. Here is one way to proceed.
One simple way to proceed is to re-examine the two criteria we have been using, and then state a generality about what to do in the event of a conflict. That generality is: use the chair, and then fit the groups as best you can. That is, try to put as many of the larger groups equatorial as you can, but realize that you may not get them all equatorial.
| Figure 11 | Fig 11 shows a plausible chair conformation of cis-1,2-dichlorocyclohexane. |
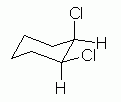 |
What have we accomplished here? First, this is the correct compound. Convince yourself that this really is cis-1,2-dichlorocyclohexane. In particular, it is cis because at each substituted position the Cl is "above" the H; that is, both Cl are on the same side of the ring.
Second, this is a proper chair. Adjacent axial groups point in opposite directions. Only two of them are shown here: the axial Cl on the upper right C is "up", and the axial H on the lower right C is "down". Thus, these aspects satisfy the proper way to orient things, in general, on a cyclohexane chair.
How good a conformation is the one shown in Fig 11? Actually, it is quite good, in this case. The actual conformation has been measured, and it follows the basic ideas shown here.
Is this the end of the story? No, but it is about enough for now. The main purpose here was to show how one must carefully look at conformation, within the constraints of the specific isomer one is trying to draw. Some compounds cannot be easily drawn within the common "rules". cis-1,2-dichlorocyclohexane is one such example. In this case, we kept the basic chair conformation, but put one larger group in the less favored axial orientation. Measurements on many such chemicals have shown that the energetic penalty of moving a cyclohexane ring much away from the basic chair conformation is quite large -- certainly larger than the energetic penalty of putting one "somewhat large" group in an axial position. Of course, with larger groups or more groups, this might not hold.
How to draw stereo bonds ("up" and "down" bonds)
There are various ways to show these orientations. The solid (dark) "up wedge" I used is certainly common. Some people use an analogous "down wedge", which is light, to indicate a down bond; unfortunately, there is no agreement as to which way the wedge should point, and you are left relying on the lightness of the wedge to know it is "down". The "down bond" avoids this wedge ambiguity, and just uses some kind of light line. The down bond I used (e.g., in Figure 5B) is a dashed line; IUPAC encourages a series of parallel lines, something like ![]() . What I did is a variation of what is recommended by IUPAC: http://www.chem.qmul.ac.uk/iupac/stereo/intro.html.
. What I did is a variation of what is recommended by IUPAC: http://www.chem.qmul.ac.uk/iupac/stereo/intro.html.
In ISIS/Draw, the "up wedge" and "down bond" that I used, along with other variations, are available from a tool button that may be labeled with any of them, depending on most recent use. It is located directly below the tool button for ordinary C-C bonds.
In Symyx Draw, the "up wedge" and "down bond", along with other variations, are available from a tool button that may be labeled with any of them, depending on most recent use. It is located directly below the "Chain" tool button.
ChemSketch provides up and down wedges, but not the simple up and down bonds discussed above. The wedges are available from the second toolbar across the top. For an expanded discussion of using these wedges, see the section of my ChemSketch Guide on Stereochemistry: Wedge bonds.
As always, the information provided on these pages in intended to help you get started. Each program has more options for drawing bonds than discussed here. When you feel the need, look around!
How to draw chairs
Most of the structures shown on this page were drawn with the free program ISIS/Draw. I have posted a guide to help you get started with ISIS/Draw. ISIS/Draw provides a simple cyclohexane (6-ring) hexagon template on the toolbar across the top. It provides templates for various 6-ring chair structures from the Templates menu; choose Rings. There are templates for simple chairs, without substituents (e.g., Fig 1B), and for chairs showing all the substituents (e.g., Fig 2B). In either case, you can add, delete, or change things as you wish. Various kinds of stereo bonds (wedges and bars) are available by clicking the left-side tool button that is just below the regular C-C single bond button. It may have a wedge shown on it, but this will vary depending on how it has been used. To choose a type of stereo bond, click on the button and hold the mouse click; a new menu will appear to the right of the button.
The free drawing program Symyx Draw, the successor to ISIS/Draw, provides similar templates and tools. A basic chair structure is provided on the default template bar that is shown. More options are available by choosing the Rings template. See my page Symyx Draw for a general guide for getting started with this program.
The free drawing program ChemSketch provides similar templates and tools. To find the special templates for chairs, go to the Templates menu, choose Template Window, and then choose "Rings" from the drop-down menu near upper left. See my page ChemSketch for a general guide for getting started with this program.
If you want to draw chair structures by hand (and if you are going on in organic chemistry, you should)... Be careful. The precise zigs and zags, and the angles of substituents are all important. Your textbook may offer you some hints for how to draw chairs. A short item in the Journal of Chemical Education offers a nice trick, showing how the chair can be thought of as consisting of an M and a W. The article is V Dragojlovic, A method for drawing the cyclohexane ring and its substituents. J Chem Educ 78:923, 7/01. (I thank M Farooq Wahab, Chemistry, Univ Karachi, for suggesting that this article be noted here.)
Aside from drawing the basic chair, the key points in adding substituents are:
- Axial groups alternate up and down, and are shown "vertical".
- Equatorial groups are approximately horizontal, but actually somewhat distorted from that, so that the angle from the axial group is a bit more than a right angle -- reflecting the common 109 degree bond angle.
- As cautioned before, it is usually easier to draw and see what is happening at the four corners of the chair than at the two middle positions. Try to use the corners as much as possible.
Other ring sizes
The main issues raised here for showing cis and trans hold for other ring sizes. Specifically, Figure 5 (parts A and B) holds for other ring sizes. The only difference would be the geometric figure used to show the ring. Discussion of conformation is more complex, and must be considered for each ring size. The "chair" is a likely conformation for 6-rings, but not for other sizes. Discussing conformations for other ring sizes is beyond the scope of this page. 6-rings are among the most common, in both organic and biochemistry.
Contributors
>Robert Bruner (http://bbruner.org)