Carbonyl Group-Mechanisms of Addition
- Page ID
- 751
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Carbonyl Group is a polar functional group that is made up a carbon and oxygen double bonded together. There are two simple classes of the carbonyl group: Aldehydes and Ketones. Aldehydes have the carbon atom of the carbonyl group is bound to a hydrogen and ketones have the carbon atom of the carbonyl group is bound to two other carbons. Since the carbonyl group is extremely polar across the carbon-oxygen double bond, this makes it susceptible to addition reactions like the ones that occur in the pi bond of Alkenes, especially by nucleophilic and electrophilic attack.
Regions of Reactivity
There are three regions of reactivity for both aldehydes and ketones: the electron donating oxygen, the electron withdrawing carbon, and the carbon adjacent to the carbonyl group (labeled "alpha"). This module will only address the oxygen and electron withdrawing carbon areas of reactivity.
.bmp?revision=1&size=bestfit&width=345&height=156)
Figure 1: Regions of Reactivity
Resonance structure is defined as any of two or more possible structures of the same compound that have identical geometry but different arrangements of their paired electrons; none of the structures have physical reality or adequately account for the properties of the compound. Examination of the resonance structures of the carbonyl group clearly shows its polar nature, and highlights the areas for either electrophilic or nucleophilic attack in the addition reaction.
Figure 2: Resonance structures of the carbonyl group
Ionic Addition to Carbonyl Group
As a result of the dipole shown in the resonance structures, polar reagents such as LiAlH4 and NaBH4 (hydride reagents) or R'MgX (Grignard reagent) will reduce the carbonyl groups, and ultimately convert unsaturated aldehydes and ketones into unsaturated alcohols. Since these reagents are extremely basic, their addition reactions are irreversible.
There are, however, addition reactions with less basic nucleophiles such as water, thiols, and amines that are capable of establishing equilibria or reversible reactions. These less basic reagents can react with the carbonyl group via two pathways: nucleophilic addition-protonation and electrophilic addition-protonation.
Nucleophilic Addition-Protonation
Under neutral or basic conditions, nucleophilic attack of the electrophilic carbon takes place. As the nucleophile approaches the electrophilic carbon, two valence electrons from the nucleophile form a covalent bond to the carbon. As this occurs, the electron pair from the pie bond transfers completely over to the oxygen which produces the intermediate alkoxide ion. This alkoxide ion, with a negative charge on oxygen is susceptible to protonation from a protic solvent like water or alcohol, giving the final addition reaction.
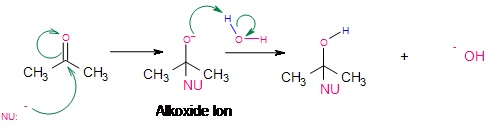
Figure 3: Alkoxide Ion Intermediate
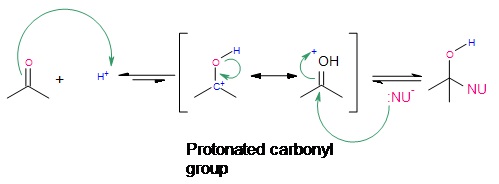
Electrophilic Addition-Protonation
Under acidic conditions, electrophilic attack of the carbonyl oxygen takes place. Initially, protonation of the carbonyl group at the oxygen takes place because of excess \(H^+\) all around. Once protonation has occurred, nucleophilic attack by the nucleophile finishes the addition reaction. It should be noted that electrophilic attack is extremely unlikely, however, a few carbonyl groups do become protonated initially to initiate addition through electrophilic attack. This type of reaction works best when the reagent being used is a very mildly basic nucleophile.
.jpg?revision=1&size=bestfit&width=499&height=184)
Figure 4: Electrophilic Addition
Outside links
References
- Vollhardt, K. P.C. & Shore, N. (2007). Organic Chemistry (5th Ed.). New York: W. H. Freeman. p. 775-777
- Otera, Junzo, ed. Modern Carbonyl Chemistry. Weinheim; Chichester: Wiley-VCH, 2000.
Problems
1. What is the best reagent to do the following conversion?
- H2/Ni
- Hg(OAc)2, H3O+
- 1. BH3, THF & 2.H2O2, NaOH
- NaBH4, THF
2. What is the Product of this reaction?
3. What is the Product of this reaction?
4. What is the Product of this reaction?
5. What is the product of this reaction?
Solutions
1. D
2.
3.
4.
5.