Alpha-carbon Reactions
- Page ID
- 1174
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Many aldehydes and ketones undergo substitution reactions at alpha carbons.
Reactions at the α-Carbon
Many aldehydes and ketones undergo substitution reactions at an alpha carbon, as shown in the following diagram (alpha-carbon atoms are colored blue). These reactions are acid or base catalyzed, but in the case of halogenation the reaction generates an acid as one of the products, and is therefore autocatalytic. If the alpha-carbon is a chiral center, as in the second example, the products of halogenation and isotopic exchange are racemic. Indeed, treatment of this ketone reactant with acid or base alone serves to racemize it. Not all carbonyl compounds exhibit these characteristics, the third ketone being an example.
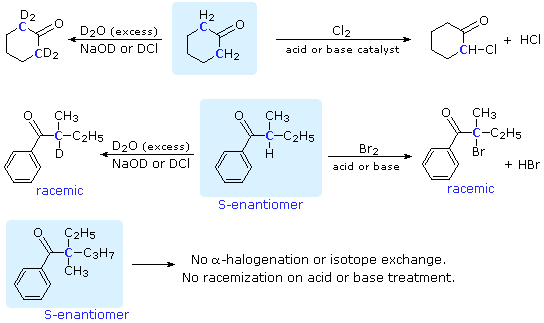
Figure 1: Reactions at the \(\alpha\) carbon
Two important conclusions may be drawn from these examples. First, these substitutions are limited to carbon atoms alpha to the carbonyl group. Cyclohexanone (the first ketone) has two alpha-carbons and four potential substitutions (the alpha-hydrogens). Depending on the reaction conditions, one or all four of these hydrogens may be substituted, but none of the remaining six hydrogens on the ring react. The second ketone confirms this fact, only the alpha-carbon undergoing substitution, despite the presence of many other sites. Second, the substitutions are limited to hydrogen atoms. This is demonstrated convincingly by the third ketone, which is structurally similar to the second but has no alpha-hydrogen.
Mechanism of Electrophilic α-Substitution
Kinetic studies of these reactions provide additional information. The rates of halogenation and isotope exchange are essentially the same (assuming similar catalysts and concentrations), and are identical to the rate of racemization for those reactants having chiral alpha-carbon units. At low to moderate halogen concentrations, the rate of halogen substitution is proportional (i.e. first order) to aldehyde or ketone concentration, but independent of halogen concentration. This suggests the existence of a common reaction intermediate, formed in a slow (rate-determining step) prior to the final substitution. Acid and base catalysts act to increase the rate at which the common intermediate is formed, and their concentration also influences the overall rate of substitution.
From previous knowledge and experience, we surmise that the common intermediate is an enol tautomer of the carbonyl reactant. Several facts support this proposal:
- Compounds that do not have any α-hydrogen atoms cannot enolize and do not undergo any of the reactions described above.
- The carbon-carbon double bond of an enol is planar, so any chirality that existed at the α carbon is lost on enolization. If chiral products are obtained from enol intermediates they will necessarily be racemic.
- In simple aldehydes and ketones enol tautomers are present in very low concentration. Reactions that involve enol reactants will therefore be limited in rate by the enol concentration. Increasing the amounts of other reactants will have little effect on the reaction rate.
- Enolization is catalyzed by acids and bases. These catalysts will therefore catalyze reactions proceeding via enol intermediates.
The reactions shown above, and others to be described, may be characterized as an electrophilic attack on the electron rich double bond of an enol tautomer. This resembles closely the first step in the addition of acids and other electrophiles to alkenes. Therefore, if electrophilic substitution reactions of this kind are to take place it is necessary that nucleophilic character be established at the alpha-carbon. A full description of the acid and base-catalyzed keto-enol tautomerization process (shown below) discloses that only two intermediate species satisfy this requirement. These are the enol tautomer itself and its conjugate base (common with that of the keto tautomer), usually referred to as an enolate anion.
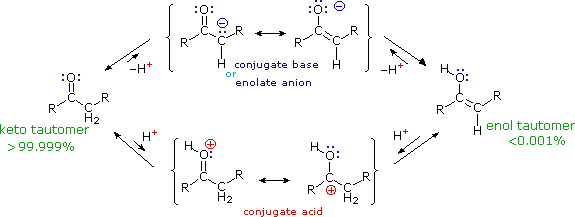
Figure 2: Keto-enol tautomerization
Clearly, the proportion of enol tautomer present at equilibrium is a critical factor in alpha substitution reactions. In the case of simple aldehydes and ketones this is very small, as noted above. A complementary property, the acidity of carbonyl compounds is also important, since this influences the concentration of the more nucleophilic enolate anion in a reaction system. Ketones such as cyclohexanone are much more acidic than their parent hydrocarbons (by at least 25 powers of ten); nevertheless they are still very weak acids (pKa = 17 to 21) compared with water. Together with some related acidities, this is listed in the following table. Even though enol tautomers are about a million times more acidic than their keto isomers, their low concentration makes this feature relatively unimportant for many simple aldehydes and ketones.
Table 1: Acidity of α-Hydrogens in Some Activated Compounds
| Compound | RCH2–NO2 | RCH2–COR | RCH2–C≡N | RCH2–SO2R |
|---|---|---|---|---|
| pKa | 9 | 20 | 25 | 25 |
In cases where more than one activating function influences a given set of alpha-hydrogens, the enol concentration and acidity is increased. Examples of such doubly (and higher) activated carbon acids are given elsewhere.
Enols and Enolate Anions
In view of these facts it may seem surprising that alpha-substitution reactions occur at all. However, we often fail to appreciate the way in which a rapid equilibrium involving a minor reactive component may spread the consequences of its behavior throughout a much larger population. Consider, for example, a large group of hungry, active hamsters running about in a big cage. Opening onto the cage there is a small annex that can hold a maximum of three hamsters. Out of two hundred hamsters in the cage, there are an average of two hamsters in the annex at any given time. The hamsters are free to enter and exit the annex, but any hamster that does so is marked by a bright red dye. Although the hamster concentration in the annex is small relative to the whole population, it will not be long before all the hamsters are dyed red. If we substitute molecules for hamsters, their numbers will be extraordinarily large (recall the size of Avogadro's number), but the equilibrium between keto tautomers (hamsters in the cage) and enol tautomers (hamsters in the annex) is so rapid that complete turnover of all the molecules in a sample may occur in fractions of a second rather than minutes or hours. The principle is the same in both cases.
Racemization and isotope exchange are due to the rapid equilibrium between chiral keto tautomers and achiral enol tautomers, as well as statistical competition between hydrogen and its deuterium isotope. For halogenation there is also a thermodynamic driving force, resulting from increased bond energy in the products. For example, the alpha-chlorination of cyclohexane, shown above, is exothermic by over 10 kcal/mole.
The Aldol Reaction
A useful carbon-carbon bond-forming reaction known as the Aldol Reaction or the Aldol Condensation is yet another example of electrophilic substitution at the alpha carbon in enols or enolate anions. Three examples of the base-catalyzed aldol reaction are shown in the following diagram, and equivalent acid-catalyzed reactions also occur. The fundamental transformation in this reaction is a dimerization of an aldehyde (or ketone) to a beta-hydroxy aldehyde (or ketone) by alpha C–H addition of one reactant molecule to the carbonyl group of a second reactant molecule. By clicking the "Structural Analysis" button below the diagram, a display showing the nucleophilic enolic donor molecule and the electrophilic acceptor molecule together with the newly formed carbon-carbon bond will be displayed. Stepwise mechanisms for the base-catalyzed and acid-catalyzed reactions may be seen by clicking the appropriate buttons.
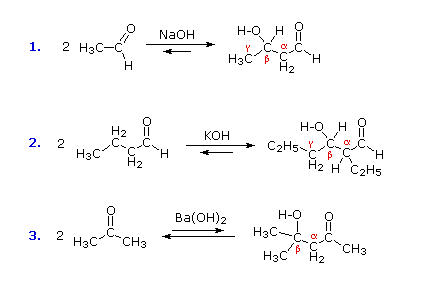
Figure 3: Aldol reaction
In the presence of acid or base catalysts the aldol reaction is reversible, and the beta-hydroxy carbonyl products may revert to the initial aldehyde or ketone reactants. In the absence of such catalysts these aldol products are perfectly stable and isolable compounds. Because of this reversibility, the yield of aldol products is related to their relative thermodynamic stability. In the case of aldehyde reactants (as in reactions #1 & 2 above), the aldol reaction is modestly exothermic and the yields are good. However, aldol reactions of ketones are less favorable (e.g. #3 above), and the equilibrium product concentration is small. A clever way of overcoming this disadvantage has been found. A comparatively insoluble base, Ba(OH)2, is used to catalyze the aldol reaction of acetone, and the product is removed from contact with this base by filtration and recirculation of the acetone.
Dehydration of Aldol Products
The products of aldol reactions often undergo a subsequent elimination of water, made up of an alpha-hydrogen and the beta-hydroxyl group. The product of this beta-elimination reaction is an α,β-unsaturated aldehyde or ketone, as shown in the following diagram. Acid-catalyzed conditions are more commonly used to effect this elimination (examples #1, 2 & 5), but base-catalyzed elimination also occurs, especially on heating (examples #3, 4 & 5). The additional stability provided by the conjugated carbonyl system of the product makes some ketone aldol reactions thermodynamically favorable (#4 & 5), and mixtures of stereoisomers (E & Z) are obtained from reaction #4. Reaction #5 is an interesting example of an intramolecular aldol reaction; such reactions create a new ring.
Reactions in which a larger molecule is formed from smaller components, with the elimination of a very small by-product such as water are termed Condensations. Hence the following examples are properly referred to as aldol condensations. The dehydration step of an aldol condensation is also reversible in the presence of acid and base catalysts. Consequently, on heating with aqueous solutions of strong acids or bases, many α, β-unsaturated carbonyl compounds fragment into smaller aldehyde or ketones, a process known as the retro-aldol reaction.
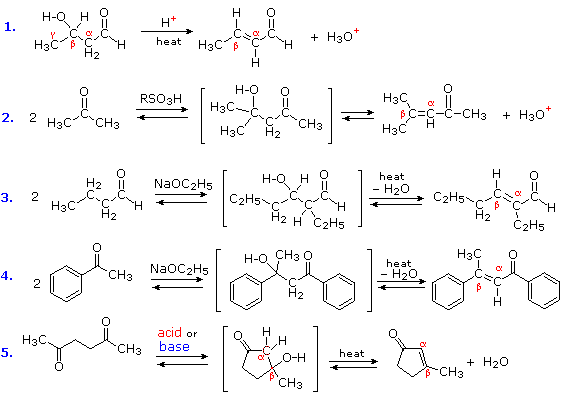
Figure 4: Aldol condensations
The acid-catalyzed elimination of water is not exceptional, since this was noted as a common reaction of alcohols. Nevertheless, the conditions required for the beta-elimination are found to be milder than those used for simple alcohols. The most surprising aspect of beta-elimination, however, is that it can be base-catalyzed. In earlier discussions we have noted that hydroxyl anion is a very poor leaving group. Why then should the base-catalyzed elimination of water occur in aldol products? To understand this puzzle we need to examine plausible mechanisms for beta-elimination, and these will be displayed by clicking the "Beta-Elimination Mechanism" button under the diagram.
As shown by the equations, these eliminations might proceed from either the keto or enol tautomers of the beta-hydroxy aldol product. Although the keto tautomer route is not unreasonable (recall the enhanced acidity of the alpha-hydrogens in carbonyl compounds), the enol tautomer provides a more favorable pathway for both acid and base-catalyzed elimination of the beta oxygen. Indeed, the base-catalyzed loss of hydroxide anion from the enol is a conjugated analog of the base-catalyzed decomposition of a hemiacetal.
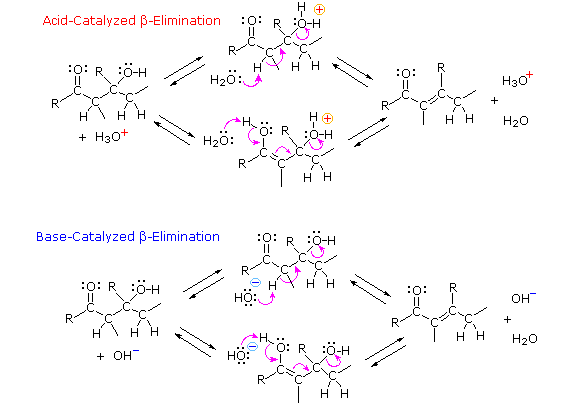
Figure 5: Beta-elimination
Mixed Aldol Condensations
The previous examples of aldol reactions and condensations used a common reactant as both the enolic donor and the electrophilic acceptor. The product in such cases is always a dimer of the reactant carbonyl compound. Aldol condensations between different carbonyl reactants are called crossed or mixed reactions, and under certain conditions such crossed aldol condensations can be effective. Some examples are shown below, and in most cases beta-elimination of water occurs under the conditions used. The exception, reaction #3, is conducted under mild conditions with an excess of the reactive aldehyde formaldehyde serving in the role of electrophilic acceptor. The first reaction demonstrates that ketones having two sets of alpha-hydrogens may react at both sites if sufficient acceptor co-reactant is supplied. The interesting difference in regioselectivity shown in the second reaction (the reactants are in the central shaded region) illustrates some subtle differences between acid and base-catalyzed aldol reactions. The base-catalyzed reaction proceeds via an enolate anion donor species, and the kinetically favored proton removal is from the less substituted alpha-carbon. The acid-catalyzed aldol proceeds via the enol tautomer, and the more stable of the two enol tautomers is that with the more substituted double bond. Finally, reaction #4 has two reactive alpha-carbons and a reversible aldol reaction may occur at both. Only one of the two aldol products can undergo a beta-elimination of water, so the eventual isolated product comes from that reaction sequence. The aldol condensation of ketones with aryl aldehydes to form α,β-unsaturated derivatives is called the Claisen-Schmidt reaction.
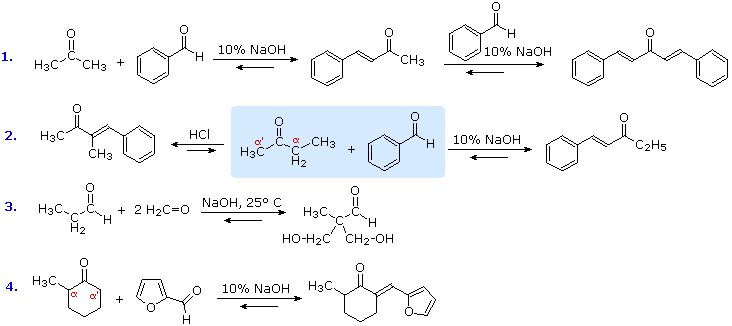
Figure 6: Claisen-Schmidt reaction
The success of these mixed aldol reactions is due to two factors. First, aldehydes are more reactive acceptor electrophiles than ketones, and formaldehyde is more reactive than other aldehydes. Second, aldehydes lacking alpha-hydrogens can only function as acceptor reactants, and this reduces the number of possible products by half. Mixed aldols in which both reactants can serve as donors and acceptors generally give complex mixtures of both dimeric (homo) aldols and crossed aldols. The following abbreviated formulas illustrate the possible products in such a case, red letters representing the acceptor component and blue the donor. If all the reactions occurred at the same rate, equal quantities of the four products would be obtained. Separation and purification of the components of such a mixture would be difficult.
ACH2CHO + BCH2CHO + NaOH  A–A + B–B + A–B + B–A
A–A + B–B + A–B + B–A
The effectiveness of the aldol reaction as a synthetic tool has been enhanced by controlling the enolization of donor compounds, and subsequent reactions with acceptor carbonyls. To see how this is done Click Here.
Irreversible Substitution Reactions
In its simplest form the aldol reaction is reversible, and normally forms the thermodynamically favored product. To fully appreciate the complex interplay of factors that underlie this important synthesis tool, we must evaluate the significance of several possible competing reaction paths.
A. The Ambident Character of Enolate Anions
Since the negative charge of an enolate anion is delocalized over the alpha-carbon and the oxygen, as shown earlier, electrophiles may bond to either atom. Reactants having two or more reactive sites are called ambident, so this term is properly applied to enolate anions. Modestly electrophilic reactants such as alkyl halides are not sufficiently reactive to combine with neutral enol tautomers, but the increased nucleophilicity of the enolate anion conjugate base permits such reactions to take place. Because alkylations are usually irreversible, their products should reflect the inherent (kinetic) reactivity of the different nucleophilic sites.
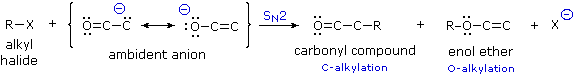
Figure 7: ambident enolates
If an alkyl halide undergoes an SN2 reaction at the carbon atom of an enolate anion the product is an alkylated aldehyde or ketone. On the other hand, if the SN2 reaction occurs at oxygen the product is an ether derivative of the enol tautomer; such compounds are stable in the absence of acid and may be isolated and characterized. These alkylations (shown above) are irreversible under the conditions normally used for SN2 reactions, so the product composition should provide a measure of the relative rates of substitution at carbon versus oxygen. It has been found that this competition is sensitive to a number of factors, including negative charge density, solvation, cation coordination and product stability.
For alkylation reactions of enolate anions to be useful, these intermediates must be generated in high concentration in the absence of other strong nucleophiles and bases. The aqueous base conditions used for the aldol condensation are not suitable because the enolate anions of simple carbonyl compounds are formed in very low concentration, and hydroxide or alkoxide bases induce competing SN2 and E2 reactions of alkyl halides. It is necessary, therefore, to achieve complete conversion of aldehyde or ketone reactants to their enolate conjugate bases by treatment with a very strong base (pKa > 25) in a non-hydroxylic solvent before any alkyl halides are added to the reaction system. Some bases having pKa's greater than 30 were described earlier, and some others that have been used for enolate anion formation are: NaH (sodium hydride, pKa > 45), NaNH2 (sodium amide, pKa = 34), and (C6H5)3CNa (trityl sodium, pKa = 32). Ether solvents like tetrahydrofuran (THF) are commonly used for enolate anion formation. With the exception of sodium hydride and sodium amide, most of these bases are soluble in THF. Certain other strong bases, such as alkyl lithium and Grignard reagents, cannot be used to make enolate anions because they rapidly and irreversibly add to carbonyl groups. Nevertheless, these very strong bases are useful in making soluble amide bases. In the preparation of lithium diisopropylamide (LDA), for example, the only other product is the gaseous alkane butane.
| C4H9–Li + butyl lithium |
[(CH3)2CH]2N–H  diisopropylamine |
[(CH3)2CH]2N(–) Li(+) + C4H10 LDA |
| O=C-C-H | + LDA  |
(–)O–C=C + [(CH3)2CH]2N–H |
Because of its solubility in THF, LDA is a widely used base for enolate anion formation. In this application one equivalent of diisopropylamine is produced along with the lithium enolate, but this normally does not interfere with the enolate reactions and is easily removed from the products by washing with aqueous acid. Although the reaction of carbonyl compounds with sodium hydride is heterogeneous and slow, sodium enolates are formed with the loss of hydrogen, and no other organic compounds are produced. The following equation provides examples of electrophilic substitution at both carbon and oxygen for the enolate anion derived from cyclohexanone.

Figure 8: Enolate anion formation
A full analysis of the factors that direct substitution of enolate anions to carbon or oxygen is beyond the scope of this text. However, an outline of some significant characteristics that influence the two reactions shown above is illustrative.
|
Reactant |
Important Factors |
|---|---|
|
CH3–I |
The negative charge density is greatest at the oxygen atom (greater electronegativity), and coordination with the sodium cation is stronger there. Because methyl iodide is only a modest electrophile, the SN2 transition state resembles the products more than the reactants. Since the C-alkylation product is thermodynamically more stable than the O-alkylated enol ether, this is reflected in the transition state energies. |
|
(CH3)3Si–Cl |
Trimethylsilyl chloride is a stronger electrophile than methyl iodide (note the electronegativity difference between silicon and chlorine). Relative to the methylation reaction, the SN2 transition state will resemble the reactants more than the products. Consequently, reaction at the site of greatest negative charge (oxygen) will be favored. Also, the high Si–O bond energy (over 25 kcal/mole greater than Si–C) thermodynamically favors the silyl enol ether product. |
B. Alkylation Reactions of Enolate Anions
The reaction of alkyl halides with enolate anions presents the same problem of competing SN2 and E2 reaction paths that was encountered earlier in the alkyl halide chapter. Since enolate anions are very strong bases, they will usually cause elimination when reacted with 2º and 3º-halides. Halides that are incapable of elimination and/or have enhanced SN2 reactivity are the best electrophilic reactants for this purpose. Four examples of the C-alkylation of enolate anions in synthesis are displayed in the following diagram. The first two employ the versatile strong base LDA, which is the reagent of choice for most intermolecular alkylations of simple carbonyl compounds. The dichloro alkylating agent used in reaction #1 nicely illustrates the high reactivity of allylic halides and the unreactive nature of vinylic halides in SN2 reactions.
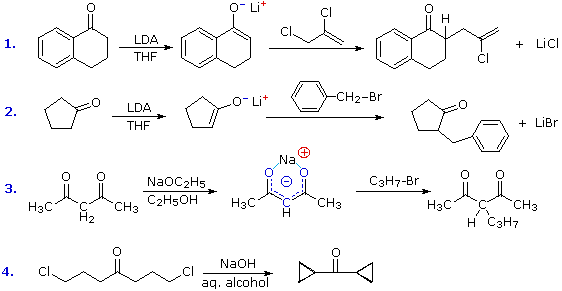
Figure 9: C-alkylation of enolate anions
The additive effect of carbonyl groups on alpha-hydrogen acidity is demonstrated by reaction #3. Here the two hydrogen atoms activated by both carbonyl groups are over 1010 times more acidic than the methyl hydrogens on the ends of the carbon chain. Indeed, they are sufficiently acidic (pKa = 9) to allow complete conversion to the enolate anion in aqueous or alcoholic solutions. As shown (in blue), the negative charge of the enolate anion is delocalized over both oxygen atoms and the central carbon. The oxygens are hydrogen bonded to solvent molecules, so the kinetically favored SN2 reaction occurs at the carbon. The monoalkylated product shown in the equation still has an acidic hydrogen on the central carbon, and another alkyl group may be attached there by repeating this sequence.
The last example (reaction #4) is an interesting case of intramolecular alkylation of an enolate anion. Since alkylation reactions are irreversible, it is possible to form small highly strained rings if the reactive sites are in close proximity. Reversible bond-forming reactions, such as the aldol reaction, cannot be used for this purpose. The use of aqueous base in this reaction is also remarkable, in view of the very low enolate anion concentration noted earlier for such systems. It is the rapid intramolecular nature of the alkylation that allows these unfavorable conditions to be used.
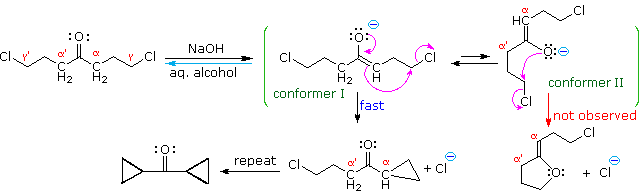
Figure 10: O-alkylation of enolate anion
The five-carbon chain of the dichloroketone can adopt many conformations, two of which are approximated in the preceding diagram. Although conformer II of the enolate anion could generate a stable five-membered ring by an intramolecular SN2 reaction, assuming proper orientation of the α and γ' carbon atoms, the concentration of this ideally coiled structure will be very low. In this case O-alkylation of the enolate anion, rather than C-alkylation, is preferred from stereoelectronic arguments (see Baldwin rules). On the other hand, conformations in which the α and γ-carbons are properly aligned for three-membered ring formation are much more numerous, the result being that as fast as the enolate base is formed it undergoes rapid and irreversible cyclization.
Ring closures to four, five, six and seven-membered are also possible by intramolecular enolate alkylation, as illustrated by the following example. In general, five and six-membered rings are thermodynamically most stable, whereas three-membered ring formation is favored kinetically.

Figure 11: Intramolecular enolate alkylation
Alternatives to Enolate Anions
Several enolate-like compounds and ions have been studied as alternative intermediates for synthesis. To learn more about these possibilities Click Here.
Contributors
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry


