VI. Rate Constants for Hydrogen-atom abstraction by Carbohydrate Radicals
- Page ID
- 23939
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)A. Extrapolating Results From Model Radicals
Radical philicity first was encountered in this chapter in the reactions of simple organic compounds (Section I.B). The assumption was that information about the reactivity of these compounds could be extrapolated to more complex ones, specifically, carbohydrates. Experimental data supported the validity of this assumption by providing examples of reactions of carbohydrate radicals that qualitatively paralleled those of simpler radicals. For instance, the reactions in eq 2 showed the cyclohexyl radical (a carbohydrate model) to be nucleophilic because it added more rapidly to electron-deficient multiple bonds than to electron-rich ones.6 A similar, nucleophilic behavior was seen in the reactions of the carbohydrate radical 26 (Scheme 2). In another example, the reactions described in equations 4 and 5 for simple organic molecules showed that polarity matching increased the rate of hydrogen-atom abstraction. Extending polarity matching to carbohydrate radicals offered a rationale for the electrophilic radical 22 abstracting an electron-rich hydrogen atom more rapidly than an electron-deficient one (Scheme 1). There is, of course, a limitation to extrapolation of results obtained from simple radicals to radicals that are more complicated. Identifying a limitation, as is done in the following section, can be useful and can lead to increased understanding of the reactivity of the more complicated radical.
B. A Limitation on Extrapolating Alkyl Radical Reactivity to Carbohydrate Radicals
Extrapolating results from reactions of structurally simple intermediates sometimes provides the only information available for judging reactivity of more complex ones. Successful extrapolation builds confidence in the models selected, but since model systems by their very nature have limitations, such extrapolation is always subject to some uncertainty. The reaction shown in eq 9 illustrates the need for caution in projecting reactivity from a simple to a more complex radical. The data in Table 2 show that rate constants for hydrogen-atom abstraction from compounds with H–Sn, H–S, and H–Si bonds are essentially independent of whether the abstracting radical is primary, secondary, or tertiary. (Steric factors have little effect on rate constants for hydrogen abstracttion.41) Extending this reactivity pattern to compounds with H–Se bonds and knowing that the rate constant for hydrogen-atom abstraction from C6H5SeH by the primary radical 27 is 2.1 x 109 M-1s-1 at 25 oC14 leads to the prediction that the rate constant for reaction of the pyranos-1-yl radical 9 with C6H5SeH should have a similar value. It does not; the value is far smaller (3.6 x 106 M‑1s-1 at 78 oC).15
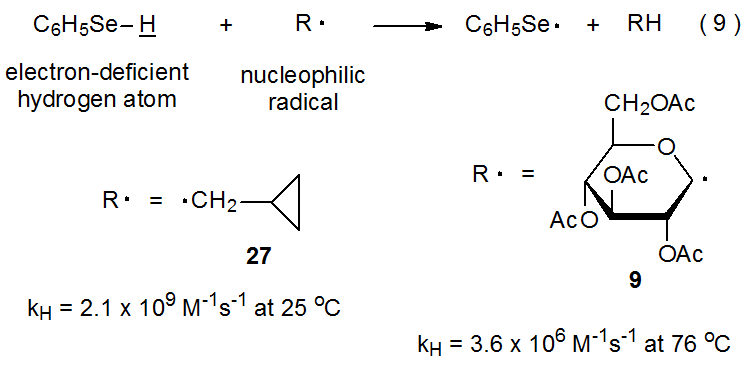.png?revision=1&size=bestfit&width=380&height=187)
C. An Explanation for Unsuccessful Extrapolation: Loss of Transition-State Stabilization
In attempting to understand the smaller-than-expected rate constant for hydrogen-atom abstraction by the radical 9, it is useful to recall from Chapter 6 (Section IV.A.2.c) that the conformation of pyranos-1-yl radicals depends on the quasi-anomeric effect, that is, on the stabilizing interaction of the σ* orbital of the C2–O bond with the p-type orbitals on the ring oxygen atom and C-1. This effect is sufficiently powerful to cause 9 to adopt the otherwise unstable, boat conformation shown in Figure 12. Since quasi-anomeric stabilization can only exist in structurally complex systems, simple radicals are limited in their ability to model pyranos-1-yl radicals. The quasi-anomeric effect provides a basis for understanding the smaller-than-expected value for the rate constant for hydrogen-atom abstraction by the radical 9.
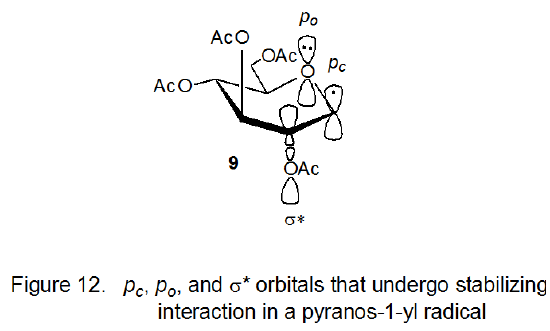
As the hydrogen-atom abstraction reaction shown in eq 9 (R· = 9) moves toward the transition state, the orbital interactions (Figure 12) that cause the electron delocalization that stabilizes the radical 9 are disappearing. (They are totally gone when the product is reached.) This loss of stabilization means that the energy of activation for hydrogen-atom abstraction by 9 will be greater than that for the radical 27, for which there is no comparable reduction in electron delocalization as the reaction progresses.15 Hydrogen-atom abstraction, in effect, forces an electron localization that causes a loss of stabilization for the delocalized radical 9 but not for the localized one 27. This decrease in stabilization at the transition state for reaction of a pyranos-1-yl radical reduces its rate constant for hydrogen-atom abstraction.
The proposal that transition-state loss of quasi-anomeric stabilization in pyranos-1-yl radicals is responsible for their reduced hydrogen-abstracting ability carries with it the prediction that carbohydrate radicals that are not so stabilized should have larger rate constants for hydrogen-atom abstraction. The quantitative information needed to evaluate this prediction does not exist, but there is qualitative information that supports the basic idea. As mentioned in Section V of Chapter 6, pyranos-1-yl radicals can be generated and observed in toluene or tetrahydrofuran but radicals centered on C-2, C-3, or C-4 (with no oxygen atom attached to the radical center and, hence, no quasi-anomeric stabilization possible) cannot be observed in these solvents because such radicals rapidly abstract hydrogen atoms from the solvent. (Only α-tetrahydrofuryl radicals are observed in reactions conducted in tetrahydrofuran and only benzyl radicals are detected in reactions in toluene.42)
The possibility that a loss of transition-state stabilization due to diminishing delocalization is responsible for a smaller-than-expected rate constant for hydrogen-atom abstraction by a pyranos-1-yl radical leads to the proposal that a similar loss of stabilization should have a similar effect on hydrogen-atom abstraction by other radicals. Rate constants for abstraction from C6H5SH have a bearing on this proposal. Simple primary, secondary, and tertiary radicals all have rate constants for hydrogen-atom abstraction from C6H5SH near 1 x 108 M-1s-1 at 25 oC (Table 2), but the rate constant for abstraction from this thiol by the benzyl radical is far smaller (3.13 x 105 M‑1s-1 25 oC).13 Because the benzyl radical loses resonance stabilization as hydrogen-atom abstraction takes place, it would be expected to parallel the pyranos-1-yl radical in having a smaller rate constant hydrogen-atom abstraction than the 1 x 108 M-1s-1 observed for unstabilized radicals. The fact that the rate constant for hydrogen-atom abstraction by the benzyl radical (3.13 x 105 M‑1s-1) is a substantially smaller than 1 x 108 M-1s-1 strengthens the diminishing-delocalization explanation for reduced reactivity of the pyranos-1-yl radical 9.

