IV. Explaining Radical Philicity

A. Valence Bond Theory

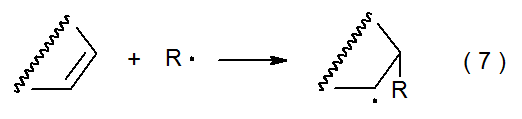
One way to explain the existence of radical philicity ­begins with the addition reaction shown in eq 7. The trans­ition-state struc­ture in this reaction can be represented as a hybrid of va­lance-bond structures. If there is no separ­ation of charge, the transition state can be represented by the contributors 3 and 4 shown in Figure 1. Unequal electron distribution at the transition state can be taken into account by including additional resonance contributors. If in the trans­i­tion state there is a transfer of electron density from R· to the C–C double bond, this transfer can be repre­sented by adding contri­butors 5 and 6 (Figure 2). If electron transfer is in the other direction, reson­ance con­tri­butors 7 and 8 (but not 5 and 6) make a significant contribution to the transition state struc­ture (Figure 2).

1. Nucleophilic Radicals

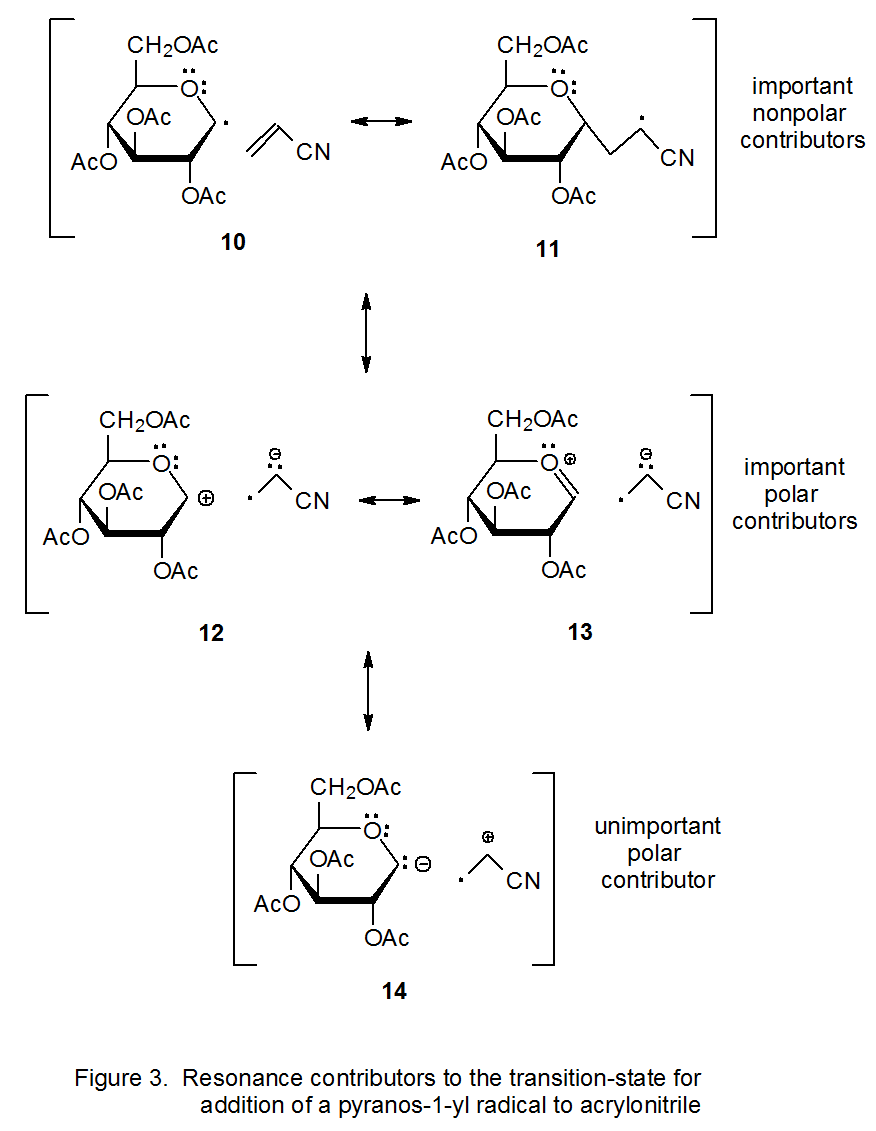
To illustrate the way in which valance bond theory explains radical nucleo­philicity, it is instruc­tive to examine the reaction shown in eq 8. In this reaction the D-gluco­pyranos-1-yl radical 9 is consid­ered to be nucleo­philic because it adds to the electron-deficient double bond in acrylo­nitrile.²⁴ The valence-bond structures 10-14 (Figure 3) all potentially contribute to the trans­i­tion-state structure in this reaction. Structures 10 and 11 are major contri­butors that have no separ­ation of charge. Struc­tures 12 and 13 are minor but signif­i­cant contributors, minor because they involve separation of charge but signif­icant because they stabilize either negative charge (12) or positive and nega­tive (13) charges effec­tively. Struc­ture 14 is not significant because it has charge-sep­aration and the charges are not effectively stabilized. Since struc­tures 12 and 13 make a greater contri­bution than does 14 to the transition state in this reaction (eq 8), the radical 9 becomes a net electron-donor at the transition state and, thus, is considered to be nucleophilic.

2. Electrophilic Radicals

If a radical center has a sufficiently strongly electron-withdrawing substit­uent (or sub­stit­u­ents) attached, the inherently nucleophilic character of a carbon-centered radical is reduced to the point that the radical becomes electro­philic.¹⁸ For example, the malonyl radical 1, which has two electron-withdrawing groups attached to the radical center, is considered to be electrophilic be­cause it adds to the electron-rich double bond in the D‑glucal 2 (eq 3).⁷ ­The electro­phi­licity of 1 can be understood primarily in terms of the impor­tance to the transition-state structure of the charge-trans­fer contributor 15, a structure in which the electron-withdraw­ing methoxy­carbonyl groups stabil­ize the negative charge and the ring oxygen atom stabilizes the positive charge (Fig­ure 4). Together these stabilizing interactions increase the contri­bution at the transition state from a structure in which the radical 1 is acting as an electrophile by accepting elec­tron density from the D-glucal 2. The reson­ance structure 16 is not an important contributor at the trans­ition state be­cause within 16 there is a destabilizing shift of electron density away from a radical center that con­tains electron-withdrawing, meth­oxy­carbonyl substit­uents.

3. Ambiphilic Radicals

Inherent in defining radical philicity in terms of electron-transfer is the idea that the philicity of a radical is a function of the reaction in question. This means that instead of describing a radical as nucleophilic, it should be des­cribed as nucleophilic in a particular reaction. It is fair to say, how­ever, that radicals that are moderately or strongly electrophilic or nucleophilic in one reaction are likely to have the same philicity in all reactions, but radicals that are weakly nucleophilic or elec­trophilic in one reaction are better candi­dates for a philicity change in a different reaction. Radi­cals that are nucleo­philic in one reaction but electrophilic in another are classified as ambiphilic.

B. Molecular Orbital Theory: Frontier-Orbital Interactions

When a transition-state structure for a reaction resembles the structure of the starting mater­ials, frontier-orbital interactions provide qualitative infor­ma­tion about energy changes taking place at the transition state. (Since fron­tier orbitals are based on the structures of the starting mater­ials, the further the transition state is along the reaction pathway the less reliable frontier-orbital inter­act­ions will be in predicting or rationalizing reactivity.) Accord­ing to Hammond’s post­ulate,²⁵ an exothermic reaction should have an early trans­ition state with a structure resembling that of the starting materials; therefore, such a reaction should be suitable for analysis by frontier-orbital inter­actions. A reaction involv­ing addition of a carbon-centered radical to a carbon–carbon double bond is a prime candidate for this type of analysis because such a reaction replaces a π bond with a more stable σ bond, a change that should produce a decidedly exo­thermic reaction.^1,3,6,26

1. Nucleophilic Radicals

A beginning point for explaining radical nucleophilicity in terms of frontier-orbital inter­ac­tions is found in Figure 5, which pictures the singly occupied molecular orbital (SOMO) in the radi­cal 17 interacting with both the π* (LUMO) and the π (HOMO) orbitals of the alkene 18. Iden­tifying the most important inter­action is critical to determining the nucleophilicity of the add­ing radi­cal. When the SOMO of 17 interacts with the alkene 18, the greater interaction is with the π* orbital of the alkene (Figure 5).⁶ Con­vinc­ing evidence supporting this position comes from plot­ting calculated HOMO and LUMO energies of substituted alkenes against the natural loga­rithm of the relative rate constants (ln k_rel) for addition of a carbon-centered radical (the tert-butyl radical was used) to these alkenes.²⁷ A linear correlation exists between ln k_rel and LUMO ener­gies, but no such correlation exists between ln k_rel and HOMO energies. The correlation with LUMO energies then is consistent with the dominant frontier-orbital interaction being between the SOMO of the radical 17 and the π* orbital of the alkene 18 (Figure 5).

The next step in understanding how frontier-orbital interactions can explain radical nucleo­phil­icity involves the addition of the radical 17 to the alkene 19, a compound in which the double bond contains the electron-withdrawing substituent Z (Figure 6). When Z replaces one of the hydro­gen atoms attached to a doubly bonded carbon atom, the π* orbital is stabil­ized and the asso­ciated energy level moves closer to that of the SOMO of 17.²⁸ This change in energy level position increases the interaction between the SOMO and the π* orbital (Figure 6). Greater inter­action trans­lates into a lower transition-state barrier for reaction; therefore, the radical 17 will add more rapidly to the alkene containing the electron-withdrawing Z group than to an unsubstituted alkene. This preferential reac­tion with electron-deficient alkenes makes the radical 17 nucleo­philic.

It is possible to increase the nucleophilicity of a carbon-centered radi­cal still further if its SOMO energy level moves even closer to that of the π* orbital of an alkene. This type of change occurs when an oxygen atom is attached directly to the radical center because interaction between the p‑type orbital on the carbon atom and the p-type orbital on the adjacent oxygen atom raises the SOMO energy level in the resulting radical (20) (Figure 7). This higher energy level places the SOMO closer ener­get­ic­ally to the π* orbital of the reactant alkene. Such a change further increases orbital inter­ac­tion and in so doing causes greater transition-state stabilization. The enhanced reac­tivity, due to the presence of the attached oxygen atom, means that the radical 20 will be even more nucleophilic than 17; thus, this oxygen-substituted radical (20) is considered to be strongly nucleophilic.

There is an additional way of viewing the frontier-orbital interaction between an alkene and a carbon-centered radical. Understanding this alternative view begins by recalling that the major, fron­tier-orbital interaction between a carbon-centered radical and an unsaturated compound is between the SOMO of the radi­cal and the π* orbital (LUMO) of the alkene (Figures 5-7). Since SOMO-LUMO inter­action is the most important and since any electron donation at the transition state resulting from this inter­action must involve electron transfer from the SOMO (the LUMO has no electrons to trans­fer), the radical is acting as an electron donor and, therefore, is behaving as a nucleo­phile.²⁹

2. Electrophilic Radicals

If a hydrogen atom attached to a carbon-centered radical is replaced by an elec­tron-with­drawing substituent (e.g., a cyano or car­bonyl group), the resulting radical becomes more elec­tro­philic.^6,18,30,31 Additional substitution of this type further increases radical electrophilicity (Fig­ure 8). The electron-withdrawing group causes the energy level associated with the singly occu­pied molec­ular orbital of the substituted radical to move to a posi­tion lower in energy; that is, the radical becomes more stable.^6,32 When the energy level of an SOMO in a carbon-centered radical becomes suf­fic­iently low, the major, frontier-orbital interaction with an alkene changes; that is, the primary interaction is no longer with the π* orbital of the alkene but rather with its π orbital (Figure 9). When this change occurs, the primary shift in electron density at the transition state is away from the filled HOMO toward the partially filled SOMO; thus, the radical is elec­tro­philic.

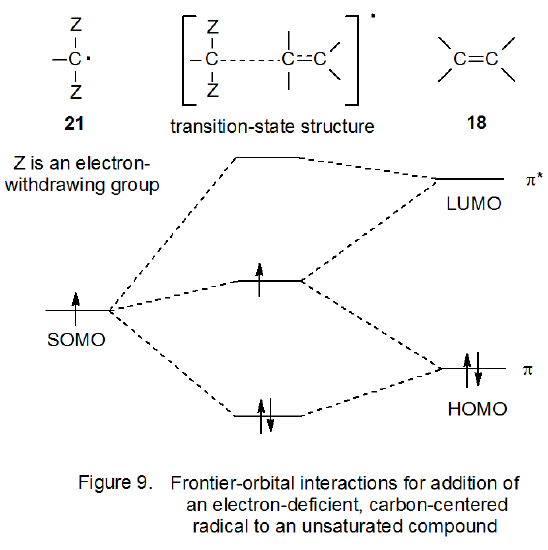
Figure 10 pictures the frontier-orbital interaction of the radical 21 with an alkene that has an electron-donating substituent. Since the HOMO for the sub­sti­tuted alkene (Figure 10) is higher in energy than the HOMO of the unsub­sti­tuted alkene (Figure 9),²⁸ transition-state stabilization from SOMO-HOMO interaction will be greater for reaction involving the substituted alkene (Figure 10). Due to this greater stabilization, the radical 21 reacts more rapidly with the more electron-rich alkene, a behavior expected from an electrophilic intermediate.

C. Balancing Polar and Enthalpy Effects

The discussion at the beginning of this chapter focused on groups of similar reactions that obey the Evans-Polanyi relation, that is, reactions in which the energies of activation can be deter­mined from reaction enthalpies using eq 1. Attention then turned to reactions where this sim­ple relation (eq 1) does not hold. The energies of activation for reactions that do not obey the Evans-Polanyi relation are influenced by polar effects operative at the trans­ition state. Since some reactions are more subject to enthalpy effects and others to polar effects, the question naturally arises as to what the balance is between these two. Principal component analysis answers this question with the finding that “the dominant factors influ­encing radical addition reactions are polar effects alone for strongly nucleo­philic or strongly electrophilic radicals...and enthalpy effects alone for weakly nucleophilic or weakly electro­philic radicals”.¹⁸ For moder­ately nucleophilic or moderately electro­philic radicals both polar and enthalpy effects are important.¹⁸