1.3: Electrocyclic Reactions

Objectives

After completing this section, you should be able to:

1. Identify electrocyclic reactions including 4 pi, 6 pi, and 8 pi ring opening and closing reactions
2. Understand the orbital analysis of electrocyclic reactions
3. Draw curved arrows to illustrate electron flow for electrocyclic reactions
4. Given electrocylic starting materials, accurately predict the product including stereochemistry
5. Use retrosynthetic analysis to determine starting materials given an electrocyclic target

Key Terms

Make certain that you can define, and use in context, the key terms below.

• Conrotatory
• Disrotatory
• Nazarov reaction

Study Notes

Electrocyclic reactions are often reversible ring opening and closing reactions that cleave and form 4-, 6-, and 8-membered rings with excellent stereocontrol. (The ring opened products must contain a p orbital at every atom.) We will also learn about cationic and anionic electrocyclic reactions that enable formation of 5-membered rings. Your goal is to understand the theoretical basis of these reactions using a molecular orbital analysis and to apply these reactions in synthesis. You should focus on accurately predicting products with a focus on stereochemistry and, given a complicated product, to accurately predict the starting material used to generate it.

Chapter 1.1 provided an overview of pericyclic reactions, including electrocyclic reactions. Electrocyclic reactions are intramolecular reactions involved in the formation of rings starting from a conjugated pi system or the formation of a conjugated pi system by cleaving a ring. In ring forming reactions, a new sigma bond (shown below in magenta) is formed at the terminus of a conjugated pi system, while ring opening reactions break a sigma bond (in magenta below) to generate a fully conjugated pi system. These are important reactions but they are not nearly as synthetically useful as cycloadditions. We will begin by looking at standard ring opening and closing reactions of neutral carbon-containing compounds. We will then explore applications of ionic electrocyclic reactions including the cationic Nazarov reaction for the synthesis of 5-membered rings.

Example Electrocyclic Reactions

Building on the introduction to electrocyclic reactions presented in Chapter 1.1, we must understand the following results for the formation and cleavage of 6-membered rings. (Note: Electrocyclic reactions are only possible for 1,3-cyclohexadiene derivatives or similar heterocycles and not other 6-membered rings lacking 2 pi bonds in the correct orientation.) We can easily draw curved arrows to illustrate electron flow for these reactions, but without molecular orbital analysis, we are unable to explain the resulting stereochemistry. In the next section, we will perform this molecular orbital analysis. The following scheme also illustrates the results for 4-membered ring systems. We will see an application of electrocyclic reactions in 8-membered ring systems in one of the summary problems at the end of this chapter. (Similar reactions of larger ring systems are possible but are rare for synthetically useful applications.)

Molecular Orbital Analysis of Electrocyclic Reactions

The molecular orbital analysis for electrocyclic reactions is best understood by focusing on the molecule in its acyclic fully conjugated form. (It doesn't matter whether this is the reactant or the product.) For the 6 pi system, we must first generate the pi molecular orbitals, add pi electrons, and identify the Highest Occupied Molecular Orbital (HOMO). This is similar to the strategy we used to understand the molecular orbital basis for cycloadditions in the previous chapter; however, the only reactive orbital for electrocyclic reactions is the HOMO. The ground state and excited state molecular orbital (MO) diagrams are shown below and highlight that the ground state HOMO is psi 3 while the excited state HOMO is psi 4*. Thus, our analysis of the ground state reaction will focus exclusively on psi 3 and the excited state on psi 4*.

We will begin our analysis of the reactions shown above by looking only at the thermal conditions for the 6 pi system. How can the psi 3 MO explain the results? We must draw out the structure with the psi 3 orbital and see how it will rotate to generate positive overlap for the formation of a new sigma bond in the ring at the terminal carbons. The orbitals must rotate in opposite directions, one clockwise and one counterclockwise, to enable positive overlap and bond formation. This process is called disrotatory and provides the insight we need to explain the stereochemical outcome. Also note that the same analysis works when thinking about the ring opening reaction. The question to answer for this process is, "How will the sigma bonding orbitals rotate to yield psi 3 for the acyclic product MO?". Since this is a reversible process, the rotation must be the same for the forward or reverse reaction.

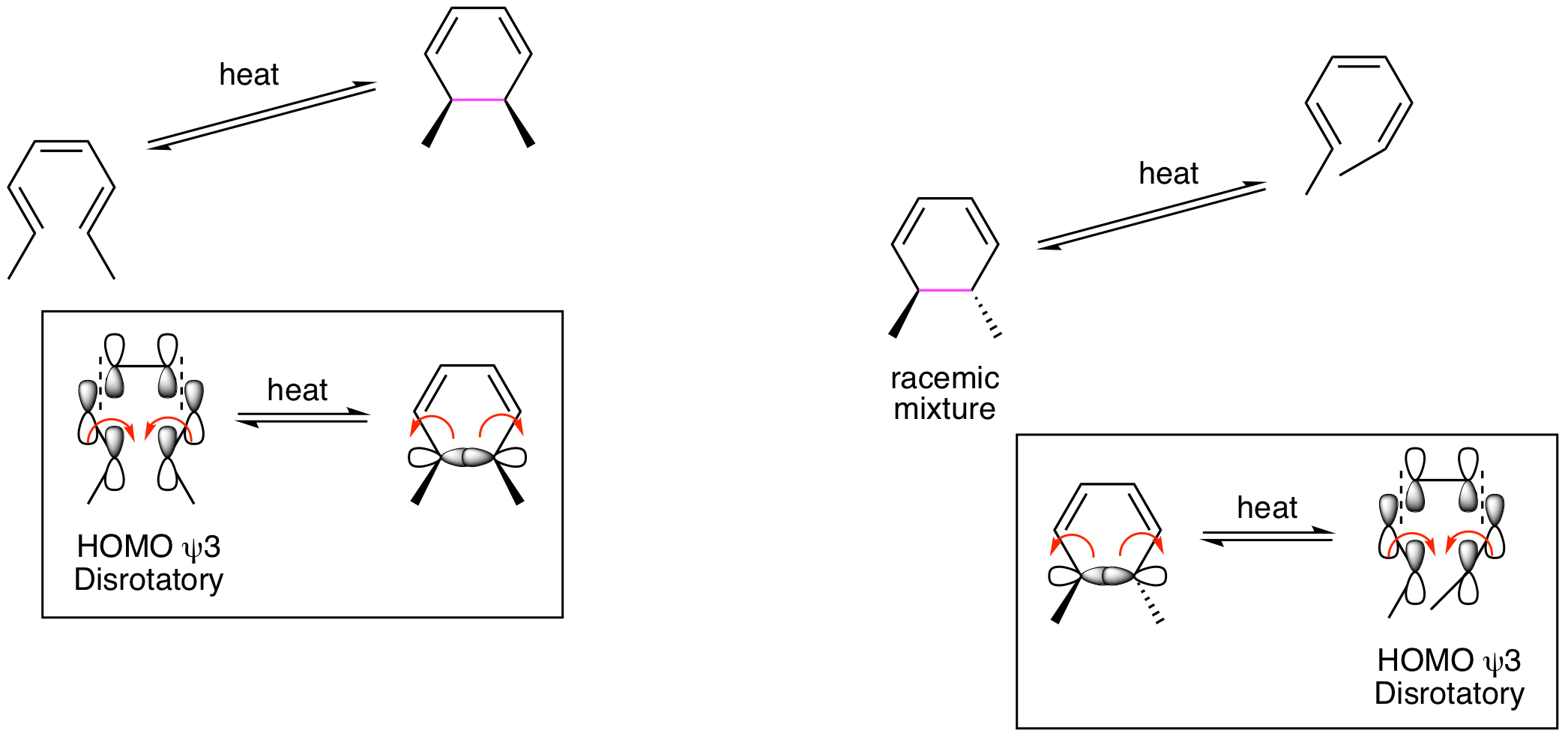
Now lets look at the photochemical reactions. As we've seen in previous chapters, light promotes a ground state electron from the HOMO to the Lowest Unoccupied Molecular Orbital (LUMO). This generates a new HOMO (the previous LUMO) in the excited state molecule. So, when analyzing the 6 pi system, we will look to psi 4* to understand the stereochemical outcomes. Contrary to the thermal reactions, the orbitals now rotate in the same direction, both clockwise or both counterclockwise, to provide positive overlap for the formation of the new sigma bond in the ring forming reaction. This is called conrotatory. For the ring opening reaction, the orbitals forming the sigma bond rotate in the same direction to generate psi 4* in the acyclic molecule. We are now able to explain the stereochemical results. Thermal and photochemical reactions yield different stereochemical results because reactions happen from different HOMOs. These different orbitals rotate by either a disrotatory or conrotatory process. If the thermal reaction is disrotatory, the photoreaction must be conrotatory, and vice versa.

Exercise \(\PageIndex{1}\)

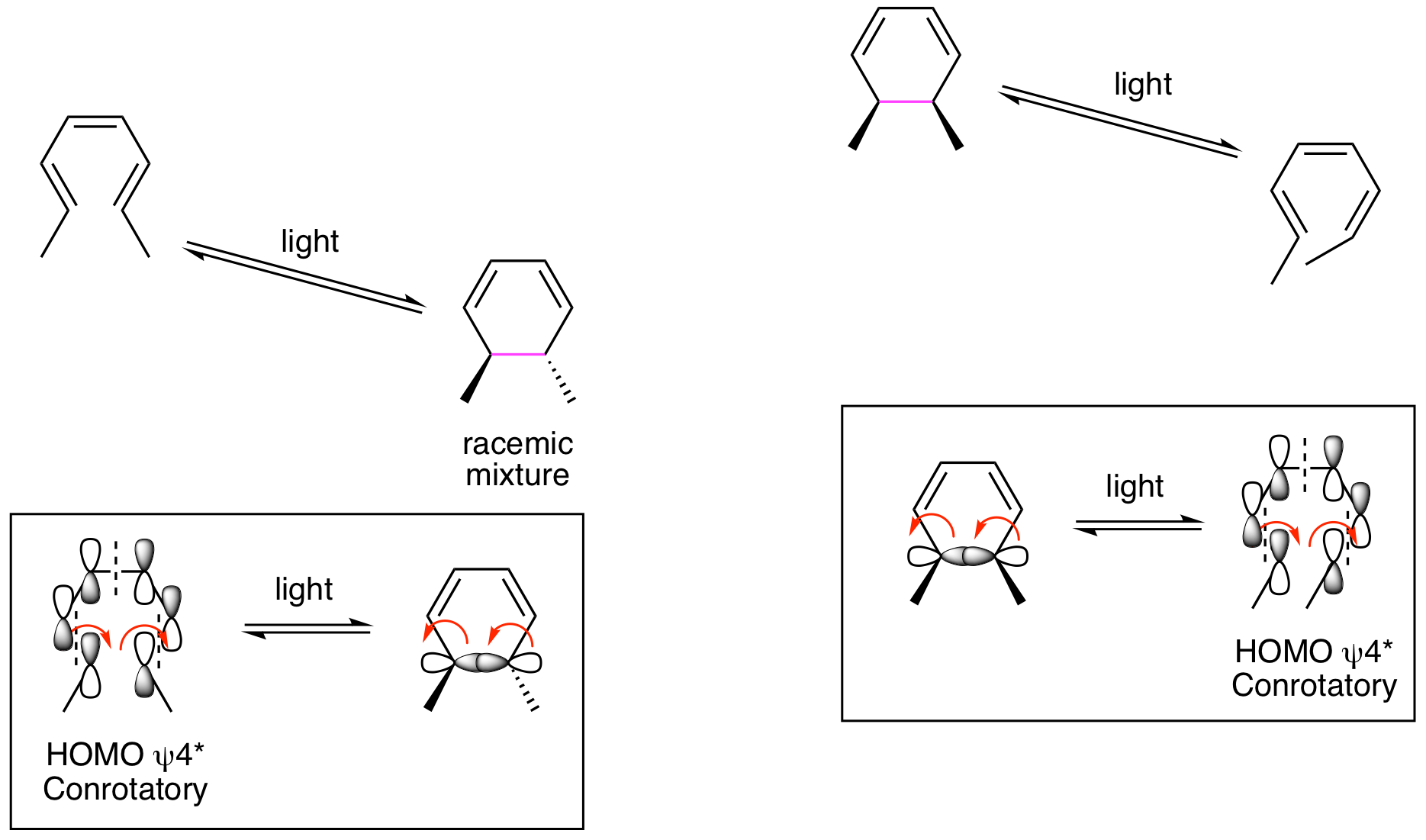
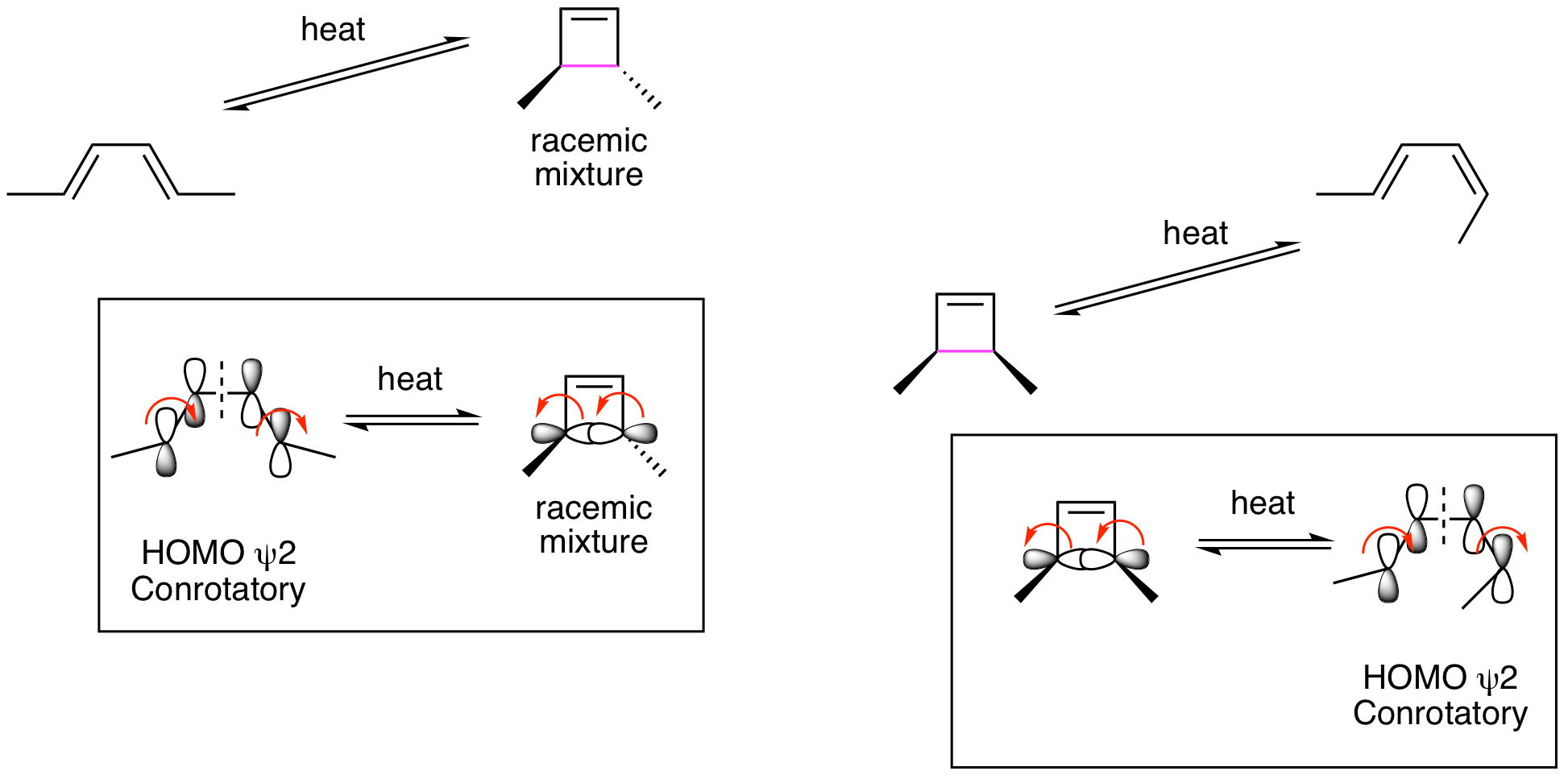
Using the same strategy illustrated above, draw out the molecular orbitals for the 4 pi reactions to explain the stereochemistry for both the thermal and photochemical reactions.

Answer

To begin, we must draw out the 4 atom pi MO diagrams to determine the ground state and excited state HOMOs.

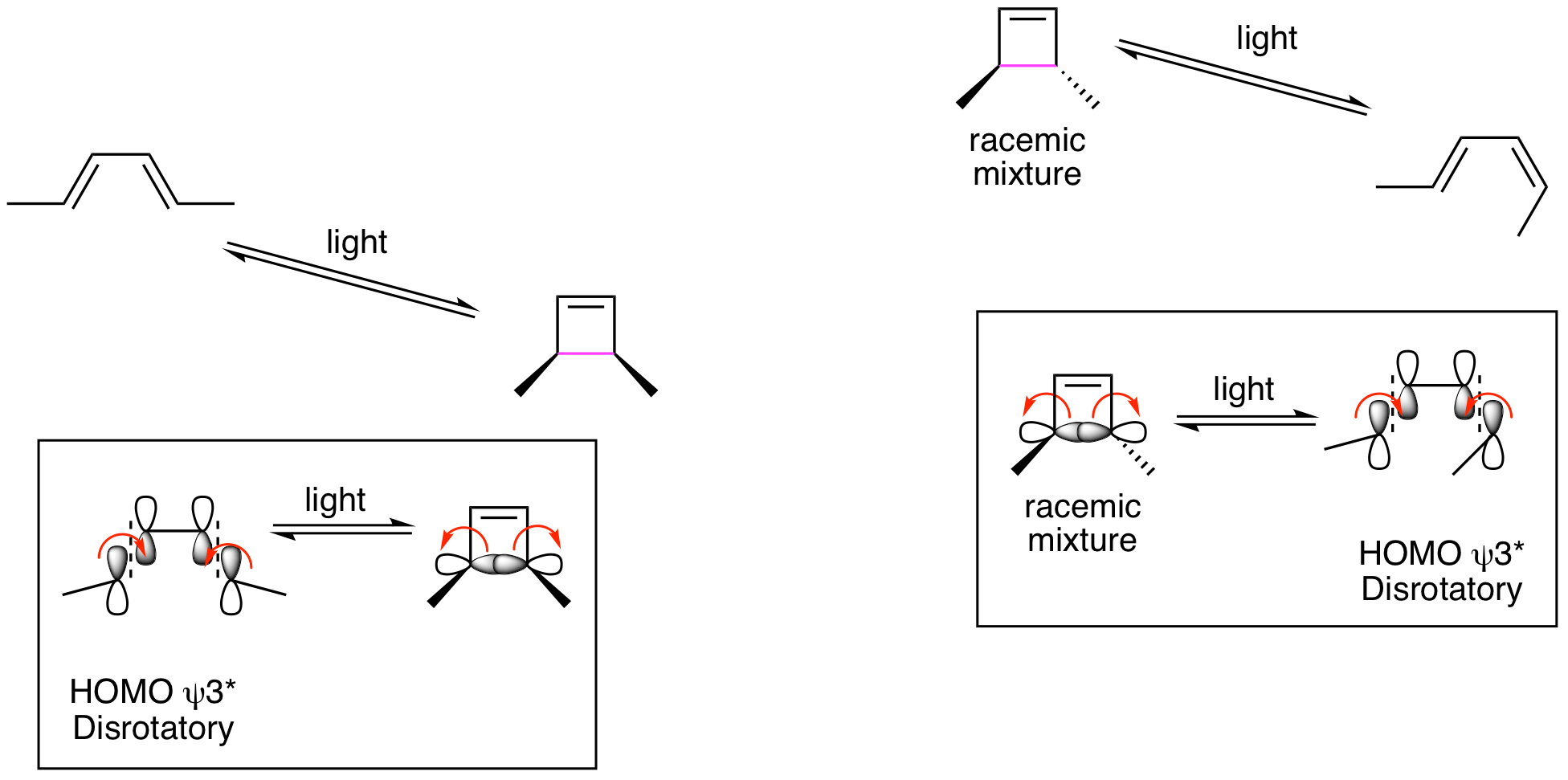
This shows that we will be analyzing HOMO psi 2 for the ground state thermal reactions and HOMO psi 3* for the excited state photoreactions. The thermal reactions are shown below and demonstrate that they are proceeding by conrotatory processes to provide the indicated stereochemistry.

This means that the photochemical reactions must be proceeding by disrotatory processes. This is illustrated below and accounts for the indicated stereochemistry.

Generalized Statement of Woodward-Hoffmann Rules for Electrocyclic Reactions

The table below provides a useful summary for electrocyclic reactions. Drawing out the key orbitals will always provide you with the correct mode of orbital rotation. However, you can use the number of electrons involved (just count your curved arrows and multiply by two) and the table below to quickly determine whether the reaction is con- or disrotatory.

Number of Electrons	Thermal	Photochemical
4n + 2	Disrotatory	Conrotatory
4n	Conrotatory	Disrotatory

Exercise \(\PageIndex{2}\)

What are the products of the following two reactions? Pay careful attention to stereochemistry.

Answer

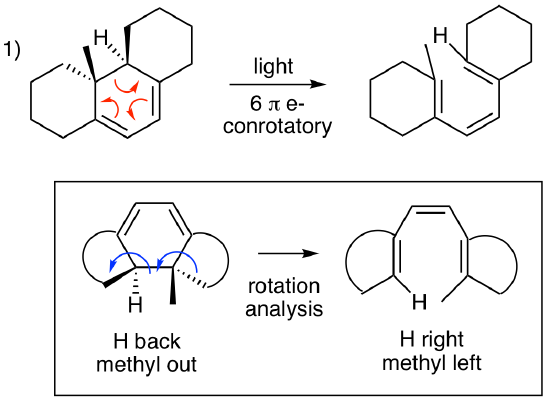
For the first problem, this is a six pi electrocyclic ring opening. Three curved arrows show that 6 electrons are involved. The central ring is the ring that reacts since it is the only ring that produces a fully conjugated pi system when it opens. The other rings are unreactive. Using the chart above, we can quickly see that this is a conrotatory process (4n+2 = 6, light). So, what is the alkene geometry in the product? We need to do a rotation analysis as illustrated in the box below. (Many students find this easiest if the bond that is breaking/forming is always on the bottom of the structure, so we have rotated the structure of the starting material and the product to make this possible.) The blue rotation arrows are going in the same direction (conrotatory). This puts the H pointing left and the methyl pointing right. When doing this analysis, we can ignore the details of the other rings which are abbreviated by the curved lines. An interesting follow up quesiton is what would happen if the starting material was heated? This would be a 6 pi disrotatory process. What would the product structure look like? This reaction doesn't happen. Why not? (This is a good question to discuss with classmates or your instructor.)

For the second problem, this is a four pi electrocyclic ring opening. Two curved arrows show that 4 electrons are involved. The four membered ring is the ring that reacts since it is the only ring that produces a fully conjugated pi system when it opens. The five membered ring is unreactive. Using the chart above, we see that this is a conrotatory process (4n = 4, heat). What is the alkene geometry in the product? Here's where this problem gets interesting. The result would be one cis alkene and one trans alkene in a 7-membered ring. What happens if you try to build this structure with your model kit? Exactly. You can't do it. There's too much strain, and the molecule doesn't exist. So, this is a trick question. (Sorry.) There is no reaction. What happens if you shine light on this molecule? Another trick question. (Again, sorry.) An isolated alkene doesn't absorb light, so a photoreaction isn't possible.

Electrocyclic Reactions of Cations (Nazarov Reaction) and Anions for the Synthesis of 5-Membered Rings

One of the most synthetically useful electrocyclic reactions is the Nazarov reaction. This is a cationic 4 pi thermal reaction (thus, conrotatory) beginning with a conjugated dienone that generates a cyclopentenone product. When thinking retrosynthetically, a cyclopentenone target is the Nazarov retron. An example of the reaction is shown below along with its mechanism. Strong acid is present to protonate the ketone in the first step. This generates a resonance stabilized cation that undergoes the requisite 4 pi ring closing reaction. This generates the cyclopentene ring that contains a resonance stabilized positive charge. The ring closing reaction initially generates two chiral centers, one of which will return to an achiral carbon upon the following E1 reaction. The mechanism ends with an acid catalyzed enol to ketone tautomerization. So, the final product is a racemic cyclopentenone where one new chiral center is present in the product.

Though much less common, anions can also participate in electrocyclic reactions. For example, deprotonating the most acidic proton in the 8-membered ring shown below with n-butyllithium results in a delocalized carbanion that undergoes a thermal 6 pi (disrotatory) ring closing reaction to form a new 5-membered ring as part of an interesting bicyclic product.

Exercise \(\PageIndex{3}\)

What happens when the starting dienone for the Nazarov reaction is not symmetrical? We explore that in this problem. Draw the two possible Nazarov reaction products and predict which will be the major product.

Answer

Following the mechanism above, we can identify the two cyclopentenone products. One contains a trisubstituted alkene while the other is a tetrasubstituted alkene. Further, working through the mechanism, the tetrasubstituted alkene product is generated from the more substituted carbocation resonance contributor. So, the major product is the more stable tetrasubstituted alkene that is generated from the more stable resonance contributor of the carbocation.

Summary Problems

Exercise \(\PageIndex{4}\)

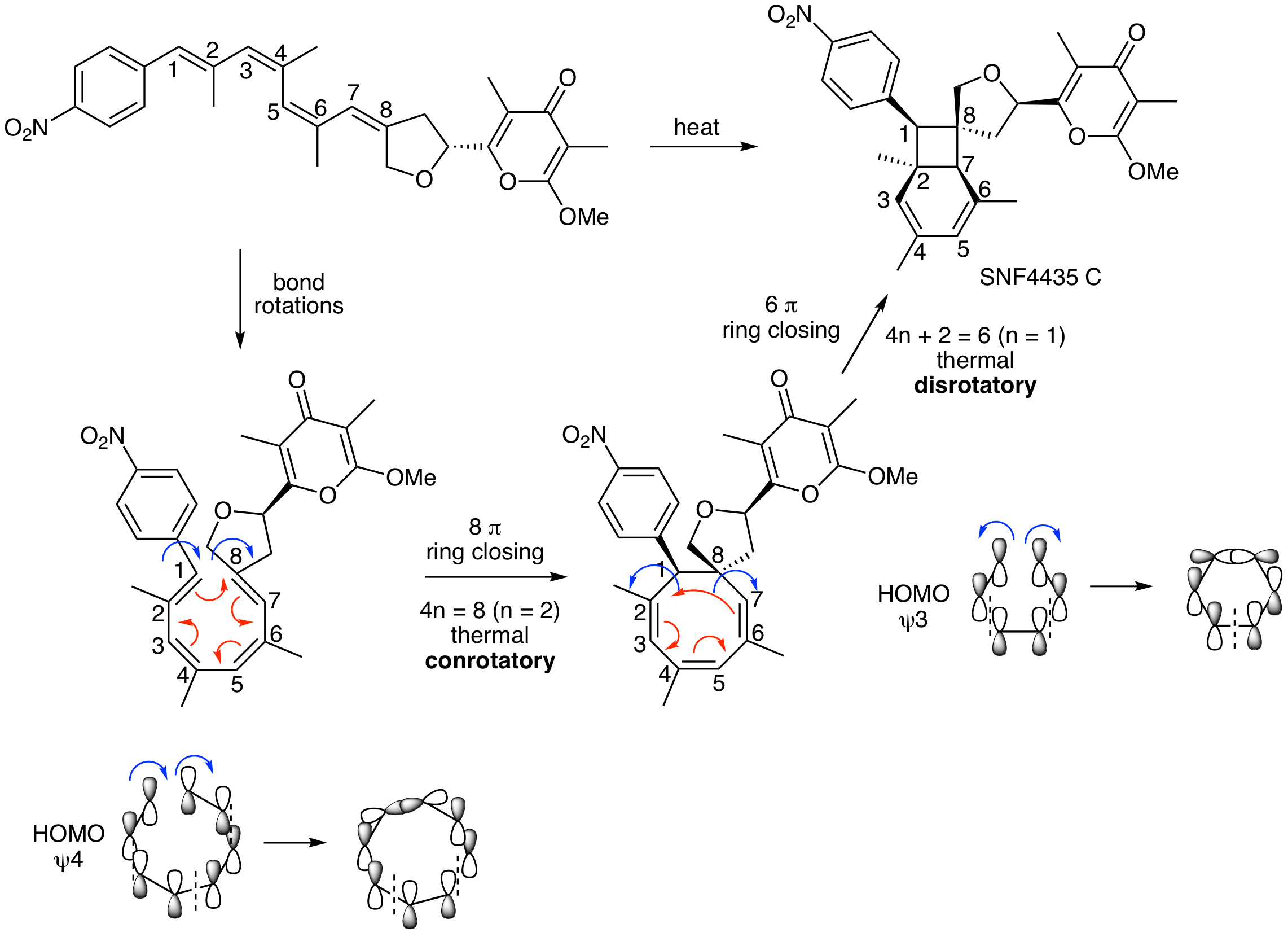
In 2005, Dirk Trauner's lab published an application of electrocyclic reactions for the synthesis of the natural product SNF4435 C. This process involves two consecutive electrocyclic reactions. Propose a mechanism for these two reactions. Clearly state what type of electrocyclic reaction is occuring, draw curved arrows, indicate if it is conrotatory or disrotatory, and draw an MO diagram for each step to explain the observed stereochemistry. The starting material is drawn exactly as depicted in the paper. The first step in your analysis is to redraw this tetraene in a reactive conformation (perform bond rotations being careful not to alter the geometry of an alkenes) so that it is more obvious what electrocyclic reactions are possible.

Answer

DOI - 10.1021/ol051790q (Organic Letters 2005)

Redrawing the starting material to place carbons 1 and 8 near each other enables you to see that the first step is a conrotatory (thermal) 8 pi electrocyclic ring closing reaction. Drawing the HOMO for this process (psi 4) illustrates that this must be conrotatory. The second reaction is a disrotatory (thermal) 6 pi ring closing reaction that occurs from HOMO psi 3. The stereochemistry agrees with these rotations.

Exercise \(\PageIndex{5}\)

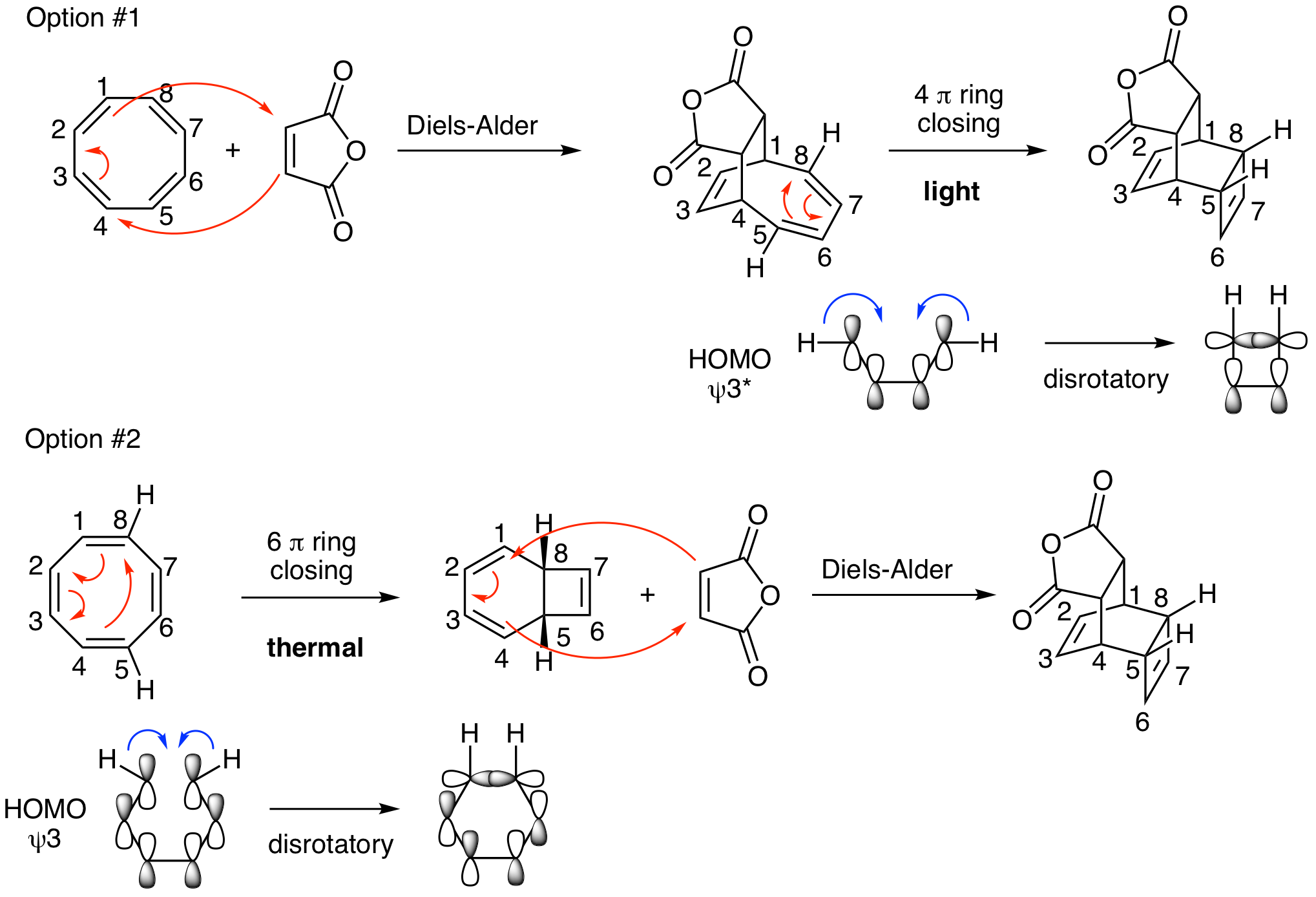
Carolyn Bertozzi is a pioneer of bioortogonal reactions. These are highly selective non-natural reactions that happen spontaneously in biological systems to label biomolecules. An interesting introduction to the work of the Bertozzi lab is described in a 2010 review entitled "Cu-free click cycloaddition reactions in chemical biology" in Chemical Society Reviews. A transformation mentioned in that review is pictured below. Propose a mechanism for this reaction. Does it happen thermally or photochemically? Justify your answer with MO diagrams. Hints: This is a two-step reaction. Both are pericyclic reactions; one is a cycloaddition and the other is an electrocyclic reaction.

DOI - 10.1039/B901970G

Answer

This problem can be approached in either the forward or reverse direction. Either way, there are two reasonable possibilities for the mechanism. The cycloaddition must be a Diels-Alder reaction which could happen in the first or second step. If the Diels-Alder happens first, the second step is a 4 pi electrocyclic ring closing reaction (Option #1). If the Diels-Alder happens second, the first step must be a 6 pi electrocyclic ring closing reaction (Option #2). Does it matter? The curved arrows look fine either way. However, as we've seen above, it is critical to analyze the stereochemistry to see what happens with reactions that are con- or disrotatory. The key piece of stereochemical information is that the Hs on carbons 5 and 8 in the product must be syn. This means that the 4 pi ring closing reaction in Option #1 must be disrotatory which requires a photochemical reaction. In Option #2, with the 6 pi ring closing happening first, it would also have to occur in a disrotatory fashion which happens with a thermal reaction. So, Option #1 is a thermal reaction (remember, Diels-Alder reactions must be thermal) followed by a photochemical reaction. Option #2 is two sequential thermal reactions. Both are possible; however, Option #2 is much more reasonable and is what actually happens in the Bertozzi lab.

Contributors

• Prof. Kevin Shea (Smith College)