1.1: Introduction to Pericyclic Reactions

Learning Objectives

After completing this section, you should be able to:

1. identify a reaction as a cycloaddition, electrocyclic reaction, or sigmatropic rearrangement.
2. draw curved arrows to explain the electron movement in a pericyclic reaction.

Key Terms

Make certain that you can define, and use in context, the key terms below.

• pericyclic reaction
• cycloaddition
• electrocyclic reaction
• sigmatropic rearrangement

Study Notes

Pericyclic reactions proceed by a rearrangement of electrons through a cyclic transition state and are distinct from polar and radical reactions that students first learn about in introductory organic chemistry. This brief chapter introduces the topic of pericyclic reactions and provides examples of the three classes of reactions. The following chapters go into depth for cycloadditions, electrocyclic reactions, and sigmatropic rearrangements.

Content

Prior to 1965, pericyclic reactions were known as "no mechanism reactions" since no one could adequately explain why reaction outcomes changed depending on whether reactants were exposed to heat or light. In 1965 Robert Burns Woodward and Roald Hoffmann used Frontier Molecular Orbital Theory, initially proposed by Kenichi Fukui, to develop their Theory of Conservation of Orbital Symmetry where outcomes of pericyclic reactions are explained by examining the Highest Occupied Molecular Orbital (HOMO) or Lowest Unoccupied Molecular Orbital (LUMO) of the reacting system. Their analysis of cycloadditions, electrocyclic reactions, and sigmatropic rearrangements is commonly referred to as the Woodward-Hoffmann Rules. A brief overview of these three reaction types is shown below and a detailed analysis is provided in the subsequent chapters.

All pericyclic reactions are concerted, they occur in one step with no intermediates formed. They are highly stereoselective, thus providing excellent methods for the synthesis of stereocenters. Product formation depends on three things: 1) Structure of the reactant, 2) Number of electrons (orbitals) involved, and 3) Conditions (heat or light). Understanding the outcome of pericyclic reactions is only possible by looking at the molecular orbitals involved, and only in-phase orbitals can overlap to form bonds during pericyclic reactions.

Cycloadditions

Cycloaddition reactions can be inter- or intramolecular and involve two different pi systems combining to form two new sigma bonds. (Cycloadditions are the only pericyclic reactions that can involve intermolecular reactions. The reverse of a cycloaddition is a cycloreversion.) They are the most convergent and synthetically useful pericyclic reactions. Common examples of cycloadditions include the Diels-Alder reaction to form 6-membered rings, dipolar cycloadditions to form 5-membered rings, and photo [2+2] cycloadditions to form 4-membered rings. Examples are shown below with the newly formed sigma bonds in the products highlighted in magenta. It is important to note that the first two examples are possible with heat while the final example only happens with light.

To understand these results, as mentioned above, we must look carefully at the pi system HOMO and LUMO involved in each reaction. An example of this is provided below. In a standard Diels-Alder reaction, an electron rich diene reacts with an electron poor dienophile, meaning the diene reacts from its pi HOMO (psi 2) while the dienophile reacts from its pi LUMO (psi 2). (Note: The dashed black lines in the figure below represent nodes in the pi molecular orbitals of the diene and dienophile.) The two new sigma bonds, shown as dashed magenta lines below, are formed from constructive overlap of the dienophile orbitals with the terminal orbitals of the diene.

We will explore a more detailed analysis of these orbital interactions in the next chapter. For now, we can summarize the most common outcomes in the table below. We should note that there is one important cycloaddition, the [2+2] thermal reaction of ketenes that does not conform to this generalized analysis.

Generalized Statement of Woodward-Hoffmann Rules for Cycloadditions

Number of Electrons	Thermal	Photochemical
4n + 2	Allowed	Forbidden
4n	Forbidden	Allowed

Electrocyclic Reactions

Electrocyclic reactions are intramolecular reactions that are ring closing (form a sigma bond) or ring opening (break a sigma bond). The key sigma bond, either formed or broken, must be at the terminus of a pi system so that either the product or reactant must be a fully conjugated diene, triene, etc. These reactions are often reversible and are classified by the number of pi electrons involved. Thus, 4 pi reactions involve the forming/breaking of 4 membered rings, 6 pi reactions involve the forming/breaking of 6 membered rings, and so on. The 4 pi and 6 pi variants are by far the most common and are illustrated below with the key sigma bond highlighted in magenta.

Electrocyclic reactions happen from the HOMO of the molecule and differ in their outcomes based on orbital rotation for the forming/breaking sigma bond. If the orbitals involved rotate in the same direction (both counterclockwise or both clockwise), the process is called conrotatory. If the orbitals involved rotate in opposite directions (one clockwise and one counterclockwise), the process is called disrotatory. These differences in rotation are critically important when stereocenters are formed or broken.

As illustrated below, treatment of the susbstituted hexatriene shown yields the cis product when heated but the trans product when treated with light. This can be explained by looking at the pi HOMO for each case. For the thermal reaction, the HOMO is psi 3 which rotates in a disrotatory fashion to yield the cis product while the trans product is formed under irradiation due to the conrotatory motion of the HOMO psi 4.

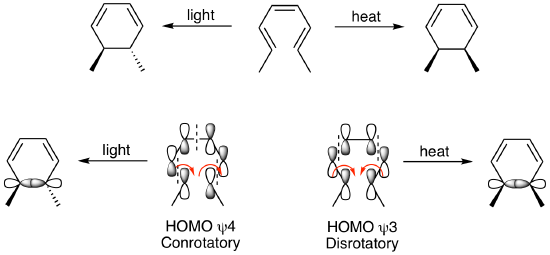
We will delve deeper into this analysis in a subsequent chapter. In general, electrocyclic reactions behave according the generalized rules outlined below.

Generalized Statement of Woodward-Hoffmann Rules for Electrocyclic Reactions

Number of Electrons	Thermal	Photochemical
4n + 2	Disrotatory	Conrotatory
4n	Conrotatory	Disrotatory

Sigmatropic Rearrangements

Sigmatropic rearrangements involve an intramolecular rearrangement of a pi system where a sigma bond in the reactant is broken and reformed in a different position in the product. The reactant and product have the same number and type of bonds, just different bond locations. The most common examples include hydrogen shifts across a diene system (called a [1,5] H shift) and rearrangements of double allyl-type systems (called [3,3] rearrangements). Sigmatropic rearrangements are labeled based on the position of the sigma bond in the reactant that is broken compared to the position of the sigma bond in the product that is formed. As shown in the examples below, the atoms on the sigma bond in the reactant that is broken (magenta bond) are both labeled "1", and the numbering of atoms on each side of that sigma bond continue until the atoms connected by the new sigma bond in the product (magenta) are reached. Thus, the H shift is [1,5] because the key sigma bond in both the reactant and product is to the H while the H moves from C-1 to C-5. For the [3,3] rearrangement, the broken sigma bond migrates across two allyl-type systems and forms between atoms "3" and "3" in the product. This particular example is a Claisen rearrangement since an allyl vinyl ether is transformed into a 1,4-carbonyl alkene.

Sigmatropic rearrangements can occur on one face of the molecule (think top or bottom, like a syn addition to an alkene) which is called a suprafacial reaction or from one face to the other (think from top to bottom or vice versa, like an anti addition to an alkene) which is called antarafacial. Suprafacial reactions are much more common. For example, a [1,5] H shift like the one shown below illustrates a hydrogen atom (s orbital) moving across a 5 atom pi system in a suprafacial fashion. The bond breaking and the bond forming, magenta dashed lines, are both on the bottom face of the pi system. Since three curved arrows are involved in the mechanism, this is a 6 pi reaction.

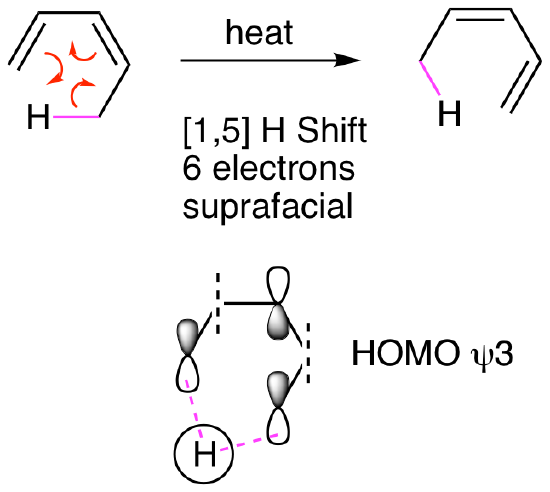
We will explore these ideas further in a subsequent chapter. The general rules for sigmatropic rearrangements are shown in the table below.

Generalized Statement of Woodward-Hoffmann Rules for Sigmatropic Rearrangements

Number of Electrons	Thermal	Photochemical
4n + 2	Suprafacial	Antarafacial
4n	Antarafacial	Suprafacial