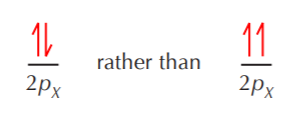2.3: Electronic Configurations
- Page ID
- 214183
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)To indicate the electronic configuration of the atom, that is to say, where the electrons reside, we use the following notation.
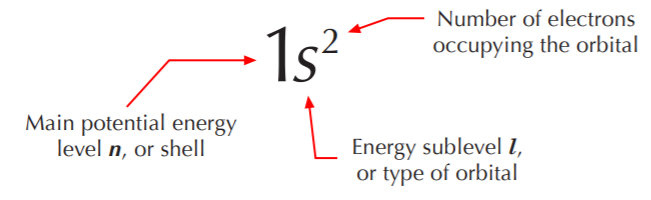
Given a periodic table, all we need to know to write the electronic configuration for a given atom is the atomic number Z, which tells us the number of electrons in the neutral atom. We start by writing the first potential energy level (n=1), then the possible types of orbitals in this level (s, p, etc.), and then the number of electrons occupying that orbital, which is always either 1or 2. It will always be 2 unless Z is an odd number and we’re down to the last electron in the valence shell. In this course we will seldom be concerned with elements beyond the second row, so we’ll keep it simple. The electronic configurations for the nonmetals of the second row are shown below.
| BORON | B | Z=5 | 1s2, 2s2, 2pX1 | Total of 5 electrons, 3 in the valence shell |
| CARBON | C | Z=6 | 1s2, 2s2, 2pX1, 2pY1 | Total of 6 electrons, 4 in the valence shell |
| NITROGEN | N | Z=7 | 1s2, 2s2, 2pX1, 2pY1, 2pZ1 | Total of 7 electrons, 5 in the valence shell |
| OXYGEN | O | Z=8 | 1s2, 2s2, 2pX2, 2pY1, 2pZ1 | Total of 8 electrons, 6 in the valence shell |
| FLUORINE | F | Z=9 | 1s2, 2s2, 2pX2, 2pY2, 2pZ1 | Total of 9 electrons, 7 in the valence shell |
| NEON | Ne | Z=10 | 1s2, 2s2, 2pX2, 2pY2, 2pZ2 | Total of 10 electrons, 8 in the valence shell |
We can also write electronic configurations where electrons are shown as half-arrows and potential energy levels are shown as horizontal dashes positioned at different heights to indicate those levels. The following diagram shows the electronic configuration for carbon.

The half-arrows shown together in opposite directions indicate that the electrons are paired. Single arrows indicate unpaired electrons. Notice that an empty orbital does not mean that such orbital does not exist. It only means there are no electrons in it. Given the right circumstances, it could hold electrons. This is in opposition to an orbital whose existence is not possible. For example d orbitals are not possible for second row elements and therefore are nonexistent in those elements.
Orbitals which are of exactly the same energy, such as the 2pX, 2pY, and 2pZ orbitals, are said to be degenerate.
In writing electronic configurations, we follow the Aufbau principle, Hund’s rule, and the Pauli exclusion principle.
The Aufbau principle (German for building up) makes reference to the process of building an atom from the ground up. That is to say, the manner in which electrons are placed in the atom one by one. We start by placing the first electron at the lowest potential energy level, which is the 1s orbital, and then following with the rest of the electrons always placing them at the lowest available level of potential energy. In other words, electrons always go into orbitals with the lowest possible energy.
Hund’s rule says that when electrons go into degenerate orbitals, they occupy them singly before pairing begins. That’s the reason why in the carbon atom shown in the previous page, the electrons in the 2pX and 2pY orbitals are placed one in each orbital, unpaired, rather than two in one orbital and paired.

Finally, the Pauli exclusion principle states that only electrons with opposite spins can occupy the same orbital. In other words, if two electrons must go into the same orbital, they must be paired. In the example shown above we have