25.4: Configurations of Aldoses

Objectives

After completing this section, you should be able to

1. draw the structures of all possible aldotetroses, aldopentoses, and aldohexoses, without necessarily being able to assign names to the individual compounds.
2. draw the Fischer projection of D-glyceraldehyde, D-ribose and D-glucose from memory.

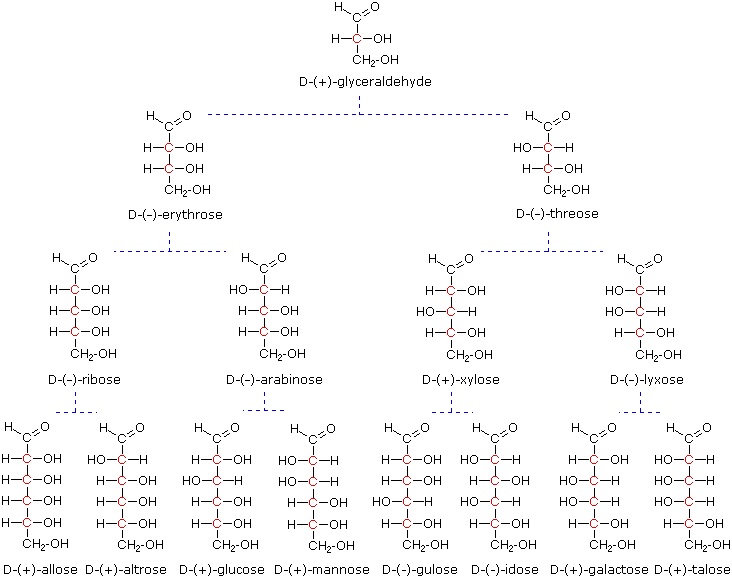
The four chiral centers in glucose indicate there may be as many as sixteen (2⁴) stereoisomers having this constitution. These would exist as eight diastereomeric pairs of enantiomers, and the initial challenge was to determine which of the eight corresponded to glucose. This challenge was accepted and met in 1891 by the German chemist Emil Fischer. His successful negotiation of the stereochemical maze presented by the aldohexoses was a logical tour de force, and it is fitting that he received the 1902 Nobel Prize for chemistry for this accomplishment. At the time Fischer undertook the glucose project it was not possible to establish the absolute configuration of an enantiomer. Consequently, Fischer made an arbitrary choice for (D)-glucose and established a network of related aldose configurations that he called the D-family. The mirror images of these configurations were then designated the L-family of aldoses. To illustrate using present day knowledge, Fischer projection formulas and names for the D-aldose family (three to six-carbon atoms) are shown below, with the asymmetric carbon atoms (chiral centers) colored red.

Aldotrioses: 3 carbon sugars with one chiral center. Aldotrioses have two (2¹) possible stereoisomers. A pair of enantiomers called D-gylceraldehyde and L-glyceraldehyde.

Aldotetroses: 4 carbon sugars with two chiral centers. Aldotetroses have four (2²) possible stereoisomers. Two pairs of D/L enantiomers called erythrose and threose.

Aldopentoses: 5 carbon sugars with three chiral centers. Aldopentoses have eight (2³) possible stereoisomers. Four pairs of D/L enantiomers called ribose, arabinose, xylose, and lyxose.

Aldohexoses: 6 carbon sugars with four chiral centers. Aldohexoses have sixteen (2⁴) possible stereoisomers. five pairs of D/L enantiomers called allose, altrose, glucose, mannose, gulose, idose, galactose, and talose.

Below are the Fischer projects 3-6 carbon aldoses. Starting with the three carbon aldose D-glyceraldehyde, each additional carbon adds a new chiral center and doubles the number of possible stereoisomers of the D-aldoses. Remember that only D-aldoses are represented below. Each D-aldose has an L-aldose enantiomer which is not shown. The L-aldose versions can be draw by inverting all of the chiral centers in the D-aldose's Fischer projection as discussed in the previous section.

Worked Example \(\PageIndex{1}\)

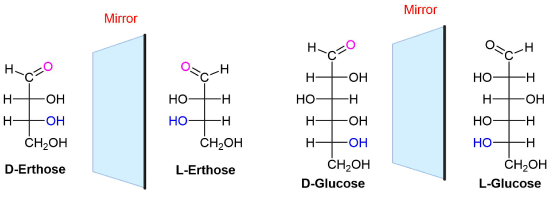
Draw the Fisher projection of L-erythrose and L-Glucose

Solution

Use the Fischer projection provided above and reverse all of the chiral centers to provide the L-sugar. Note that in both cases the D sugars have the OH going to the right on the chiral center furthest away from the carbonyl. The L-sugars have the OH going to the left.

Worked Example \(\PageIndex{2}\)

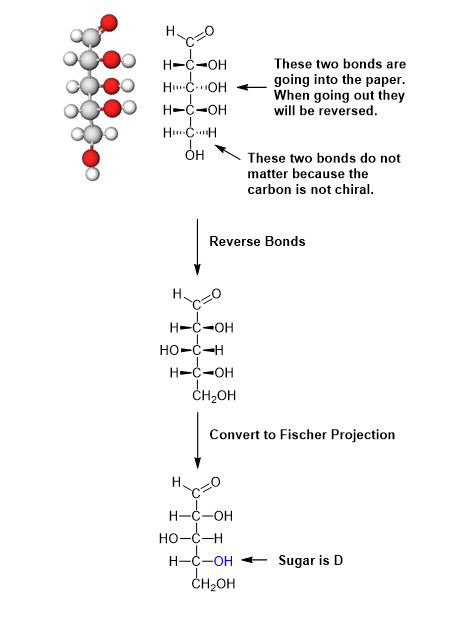
Please draw the Fischer projection fo the following aldopentose and determine if the sugars is D or L.

Solution

First, rotate the model so that the carbonyl is at the top. This is requirement of a Fischer projection. Next rotate the model so that the H and OH of the chiral carbon just below the carbonyl are facing towards you. In this orientation, a dash/wedge model will have every other set of bonds going into the plane of the page. This is not the correct orientation of a Fischer project so they must be modified. The H and OH bonds need to be coming out of the plane of the page in a Fisher projects. When converting bonds from going into the page to going out of the page the orientation of the H and OH are reversed. Remember that the last -CH₂OH of a sugar is achiral so the orientation does not need to be shown. Once the bonds are oriented correctly the wedge bonds can be converted to those of a Fischer projection.

Exercise \(\PageIndex{1}\)

For the following model of a sugar, please draw its Fischer projection and name it.

Answer

D-Mannose

Exercise \(\PageIndex{2}\)

How many heptose stereoisomers would there expected to be? How many would be D-Sugars?

Answer

There would be 2⁵ = 32 heptose stereoisomers. Half of these would be D-sugars or 16.

Exercise \(\PageIndex{3}\)

Draw the Fischer projection of the following sugars.

1. L-Ribose
2. L-Galactose
3. L-Talose

Answer

a)

b)

c)