2.8: Predicting Acid-Base Reactions from pKa Values
- Page ID
- 31391
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
After completing this section, you should be able to
- use pKa values to calculate Keq
- use pKa values to predict the equilibrium direction of an acid-base reaction.
Make certain that you can define, and use in context, the key term below.
- pKa
Using pKa values to predict reaction Equilibria
By definition, the pKa value tells us the extent to which an acid will react with water as the base, but by extension, we can also calculate the equilibrium constant for a reaction between any acid-base pair. Mathematically, it can be shown that:
Keq (for the acid base reaction in question) = 10ΔpKa
where \(ΔpK_a\) is the \(pK_a\) of product acid minus \(pK_a\) of reactant acid
Consider a reaction between methylamine and acetic acid:
First, we need to identify the acid species on either side of the equation. On the left side, the acid is of course acetic acid, while on the right side the acid is methyl ammonium. The specific pKa values for these acids are not on our very generalized pKa table, but are given in the figure above. Without performing any calculations, you should be able to see that this equilibrium lies far to the right-hand side: acetic acid has a lower pKa, is a stronger acid, and thus it wants to give up its proton more than methyl ammonium does. Doing the math, we see that
\[K_{eq} = 10^{ΔpK_a} = 10^{10.6 – 4.8} = 10^{5.8} = 6.3 \times 10^5 \nonumber \]
So \(K_{eq}\) is a very large number (much greater than 1) and the equilibrium lies far to the right-hand side of the equation, just as we had predicted.
If you had just wanted to approximate an answer without bothering to look for a calculator, you could have noted that the difference in pKa values is approximately 6, so the equilibrium constant should be somewhere in the order of 106, or one million. Using the pKa table in this way, and making functional group-based pKa approximations for molecules for which we don’t have exact values, we can easily estimate the extent to which a given acid-base reaction will proceed.
Show the products of the following acid-base reactions, and estimate the value of Keq. Use the pKa table from Section 2.8 and/or from the Reference Tables.
- Answer
- The pKa of water is 14.0. Thus the Keq for reaction d) is ~ 104.
Exercises
Use the pKa table from Section 2.8 and/or from the Reference Tables to determine if the following reactions would be expected to occur:
a) 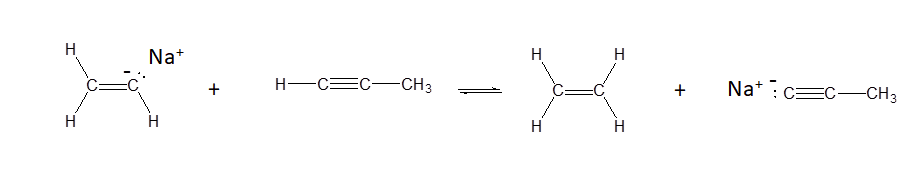
b) 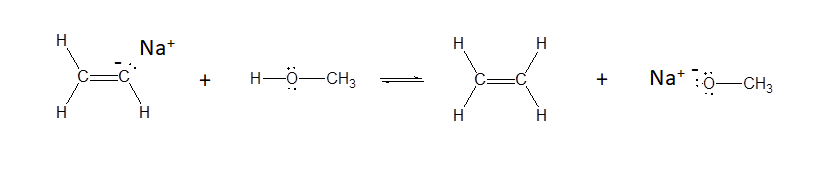
c)
- Answer
-
a) Yes - alkenes have pKa values of ~35 while alkynes have pKa values of ~25. This means that alkynes are more acidic and more likely to donate a proton.
b) Yes - alkenes have pKa values of ~35 while alcohols have pKa values of ~16-18. This means that alcohols are more acidic and more likely to donate a proton.
c) No - carboxylic acids have pKa values of ~4-5 while alcohols have pKa values of ~16-18. This means that carboxylic acids are more acidic and more likely to donate a proton (so the reverse reaction would be expected to occur).

