1.4: Electron Configurations and Electronic Orbital Diagrams (Review)

Learning Objective

Draw, interpret, and convert between Lewis (Kekule), Condensed, and Bond-line Structures

Note: The review of general chemistry in sections 1.3 - 1.6 is integrated into the above Learning Objective for organic chemistry in sections 1.7 and 1.8.

The electron configuration of an atom is the representation of the arrangement of electrons distributed among the orbital shells and subshells. Commonly, the electron configuration is used to describe the orbitals of an atom in its ground state, but it can also be used to represent an atom that has ionized into a cation or anion by compensating with the loss of or gain of electrons in their subsequent orbitals. Many of the physical and chemical properties of elements can be correlated to their unique electron configurations. The valence electrons, electrons in the outermost shell, are the determining factor for the unique chemistry of the element.

Introduction

Before assigning the electrons of an atom into orbitals, one must become familiar with the basic concepts of electron configurations. Every element on the Periodic Table consists of atoms, which are composed of protons, neutrons, and electrons. Electrons exhibit a negative charge and are found around the nucleus of the atom in electron orbitals, defined as the volume of space in which the electron can be found within 95% probability. The four different types of orbitals (s,p,d, and f) have different shapes, and one orbital can hold a maximum of two electrons. The p, d, and f orbitals have different sublevels, thus can hold more electrons.

As stated, the electron configuration of each element is unique to its position on the periodic table. The energy level is determined by the period and the number of electrons is given by the atomic number of the element. Orbitals on different energy levels are similar to each other, but they occupy different areas in space. The 1s orbital and 2s orbital both have the characteristics of an s orbital (radial nodes, spherical volume probabilities, can only hold two electrons, etc.) but, as they are found in different energy levels, they occupy different spaces around the nucleus. Each orbital can be represented by specific blocks on the periodic table. The s-block is the region of the alkali metals including helium (Groups 1 & 2), the d-block are the transition metals (Groups 3 to 12), the p-block are the main group elements from Groups 13 to 18, and the f-block are the lanthanides and actinides series.

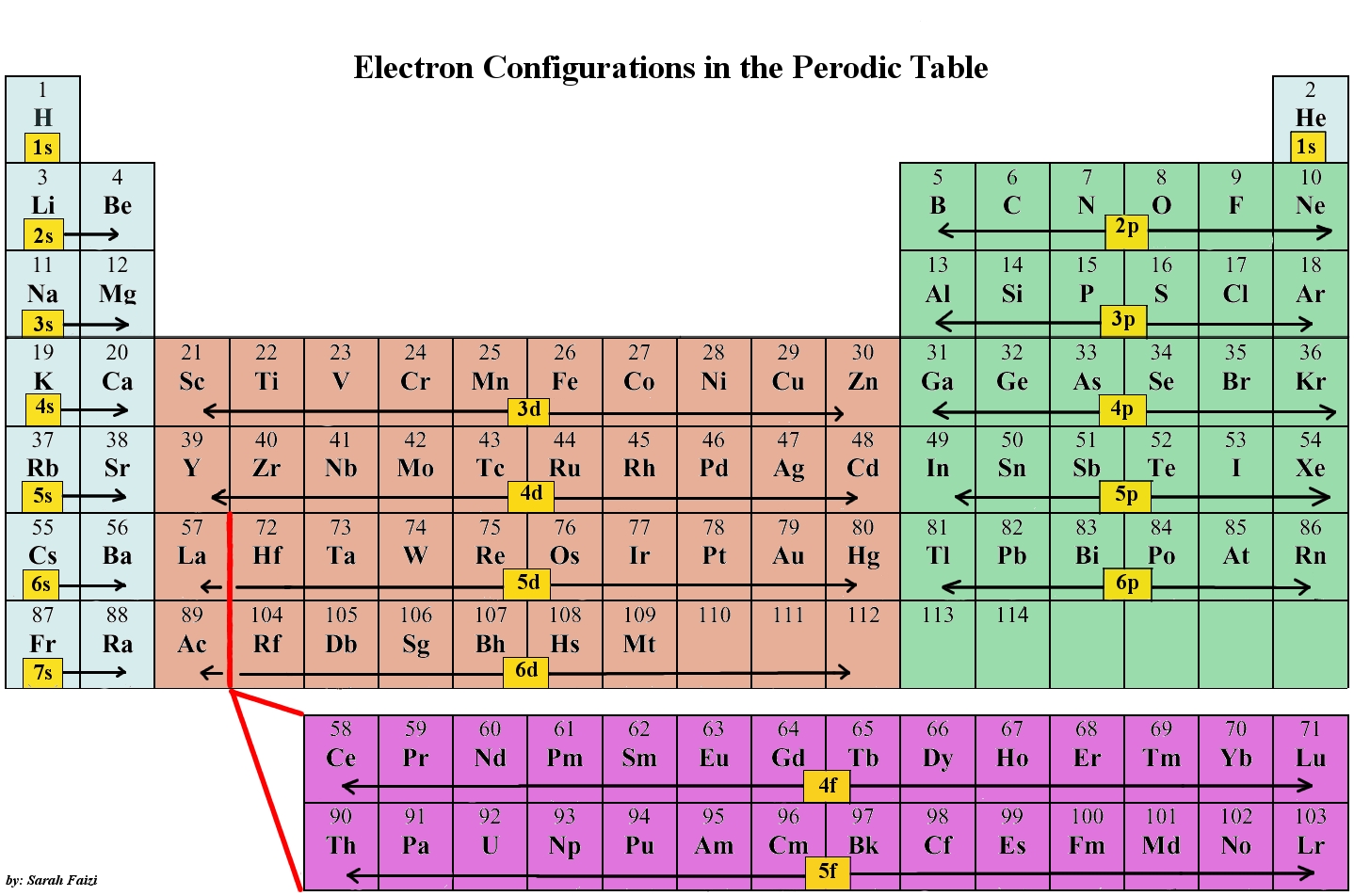
Using the periodic table to determine the electron configurations of atoms is key, but also keep in mind that there are certain rules to follow when assigning electrons to different orbitals. The periodic table is an incredibly helpful tool in writing electron configurations. For more information on how electron configurations and the periodic table are linked, visit the Connecting Electrons to the Periodic Table module.

Rules for Assigning Electron Orbitals

Occupation of Orbitals

Electrons fill orbitals in a way to minimize the energy of the atom. Therefore, the electrons in an atom fill the principal energy levels in order of increasing energy (the electrons are getting farther from the nucleus). The order of levels filled looks like this:

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, and 7p

One way to remember this pattern, probably the easiest, is to refer to the periodic table and remember where each orbital block falls to logically deduce this pattern. Another way is to make a table like the one below and use vertical lines to determine which subshells correspond with each other.

Pauli Exclusion Principle

The Pauli exclusion principle states that no two electrons can have the same four quantum numbers. The first three (n, l, and m_l) may be the same, but the fourth quantum number must be different. A single orbital can hold a maximum of two electrons, which must have opposing spins; otherwise they would have the same four quantum numbers, which is forbidden. One electron is spin up (m_s = +1/2) and the other would spin down (m_s = -1/2). This tells us that each subshell has double the electrons per orbital. The s subshell has 1 orbital that can hold up to 2 electrons, the p subshell has 3 orbitals that can hold up to 6 electrons, the d subshell has 5 orbitals that hold up to 10 electrons, and the f subshell has 7 orbitals with 14 electrons.

Example 1: Hydrogen and Helium

The first three quantum numbers of an electron are n=1, l=0, m_l=0. Only two electrons can correspond to these, which would be either m_s = -1/2 or m_s = +1/2. As we already know from our studies of quantum numbers and electron orbitals, we can conclude that these four quantum numbers refer to the 1s subshell. If only one of the m_s values are given then we would have 1s¹ (denoting hydrogen) if both are given we would have 1s² (denoting helium). Visually, this is be represented as:

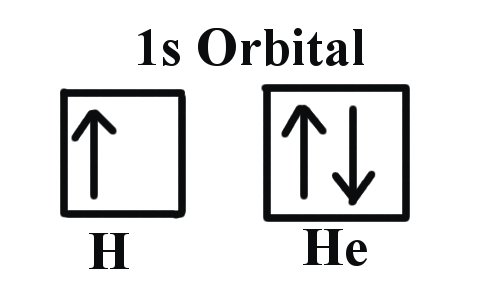
As shown, the 1s subshell can hold only two electrons and, when filled, the electrons have opposite spins.

Hund's Rule

When assigning electrons in orbitals, each electron will first fill all the orbitals with similar energy (also referred to as degenerate) before pairing with another electron in a half-filled orbital. Atoms at ground states tend to have as many unpaired electrons as possible. When visualizing this processes, think about how electrons are exhibiting the same behavior as the same poles on a magnet would if they came into contact; as the negatively charged electrons fill orbitals they first try to get as far as possible from each other before having to pair up.

Example 2: Oxygen and Nitrogen

If we look at the correct electron configuration of the Nitrogen (Z = 7) atom, a very important element in the biology of plants: 1s² 2s² 2p³

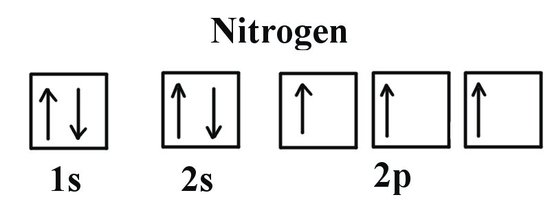
We can clearly see that p orbitals are half-filled as there are three electrons and three p orbitals. This is because Hund's Rule states that the three electrons in the 2p subshell will fill all the empty orbitals first before filling orbitals with electrons in them. If we look at the element after Nitrogen in the same period, Oxygen (Z = 8) its electron configuration is: 1s² 2s² 2p⁴ (for an atom).

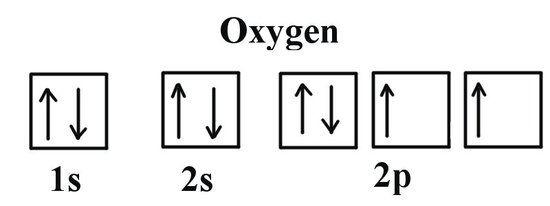
Oxygen has one more electron than Nitrogen and as the orbitals are all half filled the electron must pair up.

The Aufbau Process

Aufbau comes from the German word "aufbauen" meaning "to build." When writing electron configurations, orbitals are built up from atom to atom. When writing the electron configuration for an atom, orbitals are filled in order of increasing atomic number. However, there are some exceptions to this rule.

Example 3: 3^rd row elements

Following the pattern across a period from B (Z=5) to Ne (Z=10), the number of electrons increases and the subshells are filled. This example focuses on the p subshell, which fills from boron to neon.

• B (Z=5) configuration: 1s² 2s² 2p¹
• C (Z=6) configuration:1s² 2s² 2p²
• N (Z=7) configuration:1s² 2s² 2p³
• O (Z=8) configuration:1s² 2s² 2p⁴
• F (Z=9) configuration:1s² 2s² 2p⁵
• Ne (Z=10) configuration:1s² 2s² 2p⁶

Example

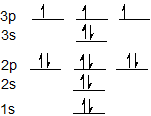
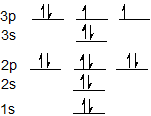
The electron configuration for sulfur is 1s² 2s² 2p⁶ 3s² 3p⁴ and can be represented using the orbital diagram below.

Exercises

Write the electron configuration for phosphorus and draw the orbital diagram.

Solution:

The electron configuration for phosphorus is 1s² 2s² 2p⁶ 3s² 3p³ and the orbital diagram is drawn below.