6.5: Thermodynamics

Equilibrium Constant

For the hypothetical chemical reaction:

\[aA + bB \rightleftharpoons cC + dD \tag{6.5.1}\]

the equilibrium constant is defined as:

\[K_C = \dfrac{[C]^c[D]^d}{[A]^a[B]^b} \tag{6.5.2}\]

The notation [A] signifies the molar concentration of species A. An alternative expression for the equilibrium constant involves partial pressures:

\[K_P = \dfrac{P_C^c P_D^d}{P_A^aP_B^b} \tag{6.5.3}\]

Note that the expression for the equilibrium constant includes only solutes and gases; pure solids and liquids do not appear in the expression. For example, the equilibrium expression for the reaction

\[CaH_2 (s) + 2H_2O (g) \rightleftharpoons Ca(OH)_2 (s) + 2H_2 (g) \tag{6.5.4}\]

is the following:

\[K_C = \dfrac{[H_2]^2}{[H_2O]^2} \tag{6.5.5}\]

Observe that the gas-phase species H₂O and H₂ appear in the expression but the solids CaH₂ and Ca(OH)₂ do not appear.

The equilibrium constant is most readily determined by allowing a reaction to reach equilibrium, measuring the concentrations of the various solution-phase or gas-phase reactants and products, and substituting these values into the Law of Mass Action.

Gibbs Energy

The interaction between enthalpy and entropy changes in chemical reactions is best observed by studying their influence on the equilibrium constants of reversible reactions. To this end a new thermodynamic function called Free Energy (or Gibbs Free Energy), symbol ΔG, is defined as shown in the first equation below. Two things should be apparent from this equation. First, in cases where the entropy change is small, ΔG ≅ ΔH. Second, the importance of ΔS in determining ΔG increases with increasing temperature.

\[ΔGº = ΔHº – TΔSº \tag{6.5.6}\]

where \(T\) is the absolute temperature measured in kelvin.

The free energy function provides improved insight into the thermodynamic driving forces that influence reactions. A negative ΔGº is characteristic of an exergonic reaction, one which is thermodynamically favorable and often spontaneous, as is the melting of ice at 1 ºC. Likewise a positive ΔGº is characteristic of an endergonic reaction, one which requires an input of energy from the surroundings.

Example 6.5.1: Decomposition of Cyclobutane

For an example of the relationship of free energy to enthalpy consider the decomposition of cyclobutane to ethene, shown in the following equation. The standard state for all the compounds is gaseous.

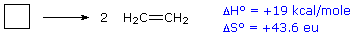
This reaction is endothermic, but the increase in number of molecules from one (reactants) to two (products) results in a large positive ΔSº.

At 25 ºC (298 ºK), ΔGº = 19 kcal/mol – 298(43.6) cal/mole = 19 – 13 kcal/mole = +6 kcal/mole. Thus, the entropy change opposes the enthalpy change, but is not sufficient to change the sign of the resulting free energy change, which is endergonic. Indeed, cyclobutane is perfectly stable when kept at room temperature.

Because the entropy contribution increases with temperature, this energetically unfavorable transformation can be made favorable by raising the temperature. At 200 ºC (473 ºK), ΔGº = 19 kcal/mol – 473(43.6) cal/mole = 19 – 20.6 kcal/mole = –1.6 kcal/mole. This is now an exergonic reaction, and the thermal cracking of cyclobutane to ethene is known to occur at higher temperatures.

\[ΔGº = –RT \ln K = –2.303RT \log K\]

with

• R = 1.987 cal/ ºK mole
• T = temperature in ºK
• K = equilibrium constant

A second equation, shown above, is important because it demonstrates the fundamental relationship of ΔGº to the equilibrium constant, K. Because of the negative logarithmic relationship between these variables, a negative ΔGº generates a K>1, whereas a positive ΔGº generates a K<1. When ΔGº = 0, K = 1. Furthermore, small changes in ΔGº produce large changes in K. A change of 1.4 kcal/mole in ΔGº changes K by approximately a factor of 10. This interrelationship may be explored with the calculator on the right. Entering free energies outside the range -8 to 8 kcal/mole or equilibrium constants outside the range 10-6 to 900,000 will trigger an alert, indicating the large imbalance such numbers imply.

Substituted Cyclohexanes​

A Values

Substituents on a cyclohexane prefer to be in the equatorial position. When a substituent is in the axial position, there are two gauche butane interactions more than when a substituent is in the equatorial position. We quantify the energy difference between the axial and equatorial conformations as the A-value, which is equivalent to the negative of the ∆G°, for the equilibrium shown below. Therefore the A-value, or -∆G°, is the preference for the substituent to sit in the equatorial position.

Recall that the equilibrium constant is related to the change in Gibbs Energies for the reaction:

\[\Delta{G^o} = -RT\ln {K_{eq}}\]

The balance between reactants and products in a reaction will be determined by the free energy difference between the two sides of the reaction. The greater the free energy difference, the more the reaction will favor one side or the other (Table 6.5.1).

Table 6.5.1: Below is a table of A-values for some common substituents.

Substituent	∆G° (kcal/mol)	A-value
-F	-0.28-0.24	0.24-0.28
-Cl	-0.53	0.53
-Br	-0.48	0.48
-I	-0.47	0.47
-CH3 (-Me)	-1.8	1.8
-CH2CH3 (-Et)	-1.8	1.8
-CH(CH3)2 (-i-Pr)	-2.1	2.1
-C(CH3)3 (-t-Bu)	<-4.5	>4.5
-CHCH2	-1.7	1.7
-CCH	-0.5	0.5
-CN	-0.25-0.15	0.15-0.25
-C6H5 (-Ph)	-2.9	2.9

Polysubstituted Cyclohexanes

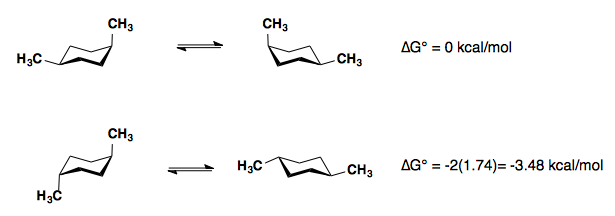
1,4-disubstitution

The A-values of the substituents are roughly additive in either the cis- or trans-diastereomers.

1,3-disubstitution

​A-values are only additive in the trans-diastereomer:

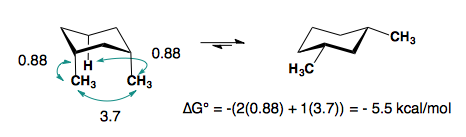
When there are cis-substituents on the chair, there is a new interaction in the di-axial conformation:

In the above example, each methyl group has one 1,3-diaxial interaction with a hydrogen. The methyl groups also interact with each other. This new diaxial interaction is extremely unfavorable based on their steric interaction (see: double-gauche pentane conformation).

Contributors

• Prof. Steven Farmer (Sonoma State University)

• William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

• Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

• Jim Clark (Chemguide.co.uk)