1.22: How Substituents Affect the Strength of an Acid
- Page ID
- 17875
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Now that we know how to quantify the strength of an acid or base, our next job is to gain an understanding of the fundamental reasons behind why one compound is more acidic or more basic than another. This is a big step: we are, for the first time, taking our knowledge of organic structure and applying it to a question of organic reactivity. Many of the ideas that we’ll see for the first here will continue to apply throughout the book as we tackle many other organic reaction types.
A: Periodic trends
First, we will focus on individual atoms, and think about trends associated with the position of an element on the periodic table. We’ll use as our first models the simple organic compounds ethane, methylamine, and ethanol, but the concepts apply equally to more complex biomolecules with the same functionalities, for example the side chains of the amino acids alanine (alkane), lysine (amine), and serine (alcohol).
Horizontal periodic trend in acidity and basicity
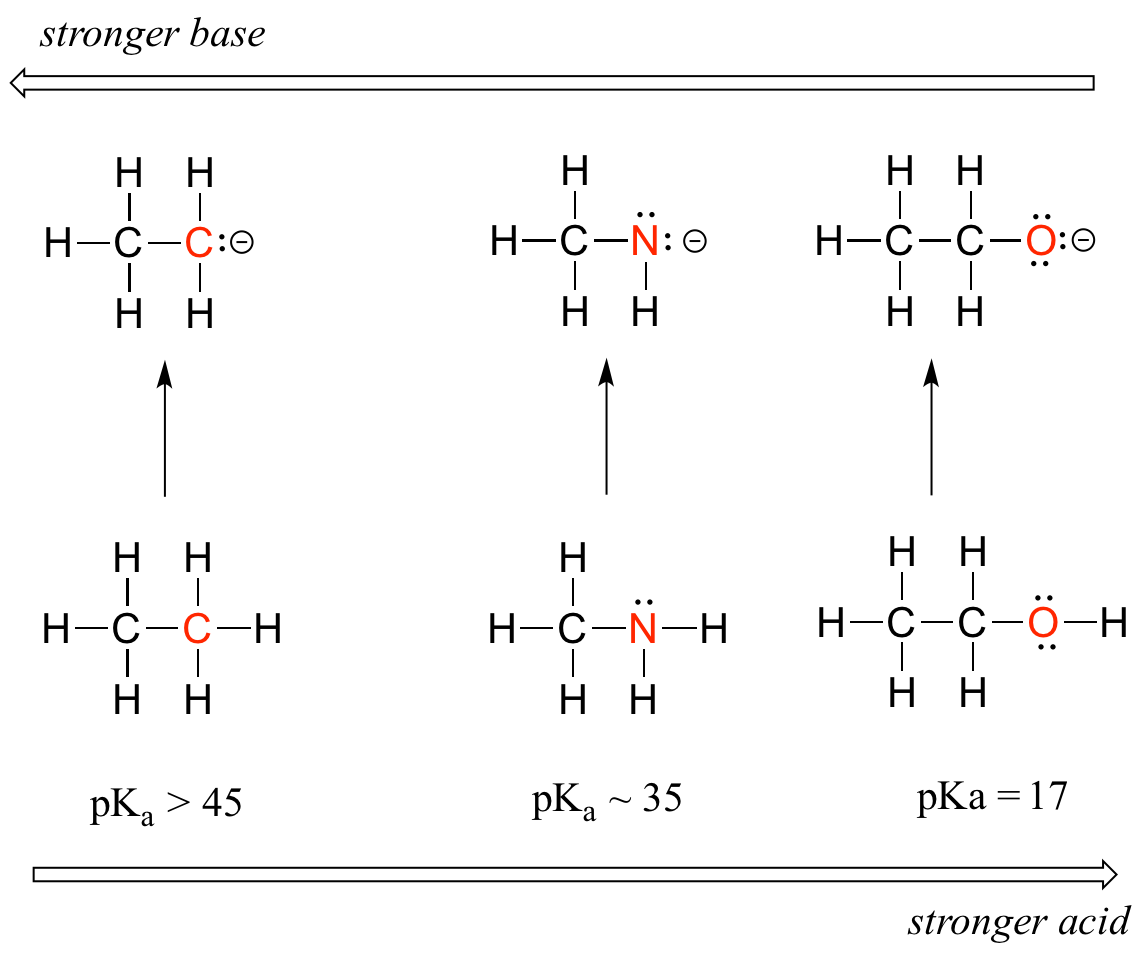
We can see a clear trend in acidity as we move from left to right along the second row of the periodic table from carbon to nitrogen to oxygen. The key to understanding this trend is to consider the hypothetical conjugate base in each case: the more stable (weaker) the conjugate base, the stronger the acid. Look at where the negative charge ends up in each conjugate base. In the conjugate base of ethane, the negative charge is borne by a carbon atom, while on the conjugate base of methylamine and ethanol the negative charge is located on a nitrogen and an oxygen, respectively. Remember that electronegativity also increases as we move from left to right along a row of the periodic table, meaning that oxygen is the most electronegative of the three atoms, and carbon the least.
The more electronegative an atom, the better able it is to bear a negative charge. Weaker bases have negative charges on more electronegative atoms; stronger bases have negative charges on less electronegative atoms.
Thus, the methoxide anion is the most stable (lowest energy, least basic) of the three conjugate bases, and the ethyl carbanion anion is the least stable (highest energy, most basic). Conversely, ethanol is the strongest acid, and ethane the weakest acid.
When moving vertically within a given column of the periodic table, we again observe a clear periodic trend in acidity. This is best illustrated with the haloacids and halides: basicity, like electronegativity, increases as we move up the column.
Vertical periodic trend in acidity and basicity
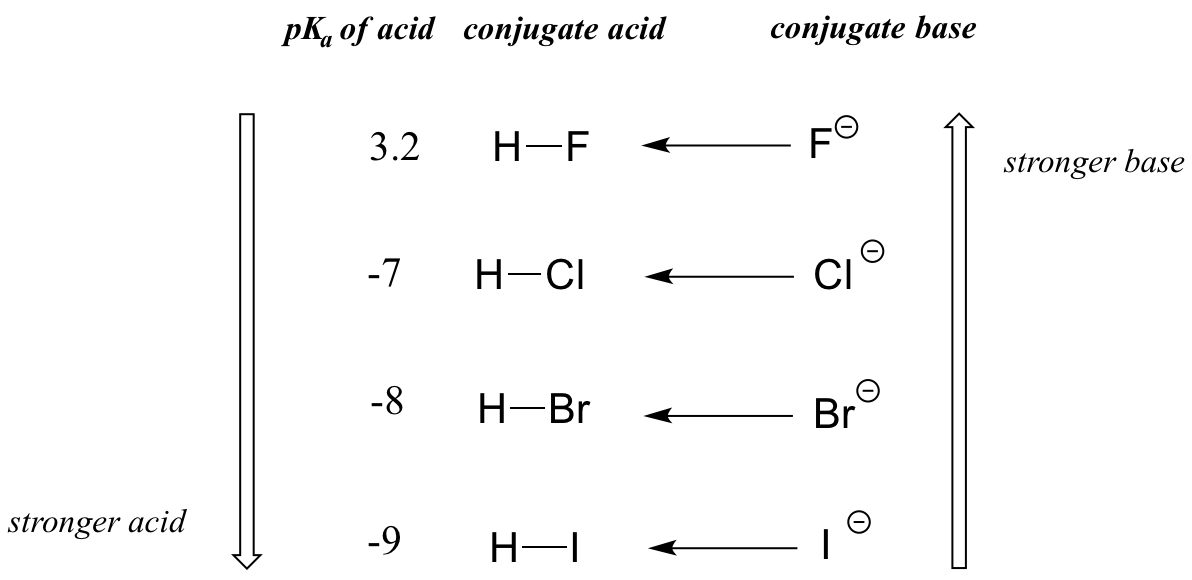
Conversely, acidity in the haloacids increases as we move down the column.
In order to make sense of this trend, we will once again consider the stability of the conjugate bases. Because fluorine is the most electronegative halogen element, we might expect fluoride to also be the least basic halogen ion. But in fact, it is the least stable, and the most basic! It turns out that when moving vertically in the periodic table, the size of the atom trumps its electronegativity with regard to basicity. The atomic radius of iodine is approximately twice that of fluorine, so in an iodide ion, the negative charge is spread out over a significantly larger volume:
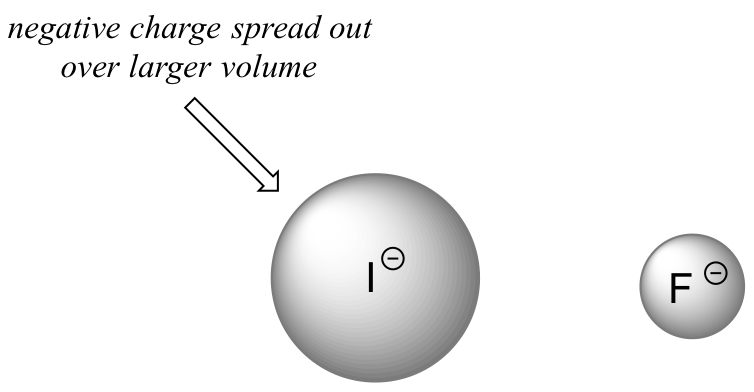
This illustrates a fundamental concept in organic chemistry:
Electrostatic charges, whether positive or negative, are more stable when they are ‘spread out’ over a larger area.
We will see this idea expressed again and again throughout our study of organic reactivity, in many different contexts. For now, we are applying the concept only to the influence of atomic radius on base strength. Because fluoride is the least stable (most basic) of the halide conjugate bases, HF is the least acidic of the haloacids, only slightly stronger than a carboxylic acid. HI, with a pKa of about -9, is almost as strong as sulfuric acid.
More importantly to the study of biological organic chemistry, this trend tells us that thiols are more acidic than alcohols. The pKa of the thiol group on the cysteine side chain, for example, is approximately 8.3, while the pKa for the alcohol group on the serine side chain is on the order of 17.
Remember the concept of 'driving force' that we learned about in chapter 6? Recall that the driving force for a reaction is usually based on two factors: relative charge stability, and relative total bond energy. Let's see how this applies to a simple acid-base reaction between hydrochloric acid and fluoride ion:
HCl + F- → HF + Cl-
We know that HCl (pKa -7) is a stronger acid than HF (pKa 3.2), so the equilibrium for the reaction lies on the product side: the reaction is exergonic, and a 'driving force' pushes reactant to product.
What explains this driving force? Consider first the charge factor: as we just learned, chloride ion (on the product side) is more stable than fluoride ion (on the reactant side). This partially accounts for the driving force going from reactant to product in this reaction: we are going from less stable ion to a more stable ion.
What about total bond energy, the other factor in driving force? If you consult a table of bond energies, you will see that the H-F bond on the product side is more energetic (stronger) than the H-Cl bond on the reactant side: 565 kJ/mol vs 427 kJ/mol, respectively). This also contributes to the driving force: we are moving from a weaker (less stable) bond to a stronger (more stable) bond.
B: Resonance effects
In the previous section we focused our attention on periodic trends - the differences in acidity and basicity between groups where the exchangeable proton was bound to different elements. Now, it is time to think about how the structure of different organic groups contributes to their relative acidity or basicity, even when we are talking about the same element acting as the proton donor/acceptor. The first model pair we will consider is ethanol and acetic acid, but the conclusions we reach will be equally valid for all alcohol and carboxylic acid groups.
Despite the fact that they are both oxygen acids, the pKa values of ethanol and acetic acid are strikingly different. What makes a carboxylic acid so much more acidic than an alcohol? As before, we begin by considering the stability of the conjugate bases, remembering that a more stable (weaker) conjugate base corresponds to a stronger acid.
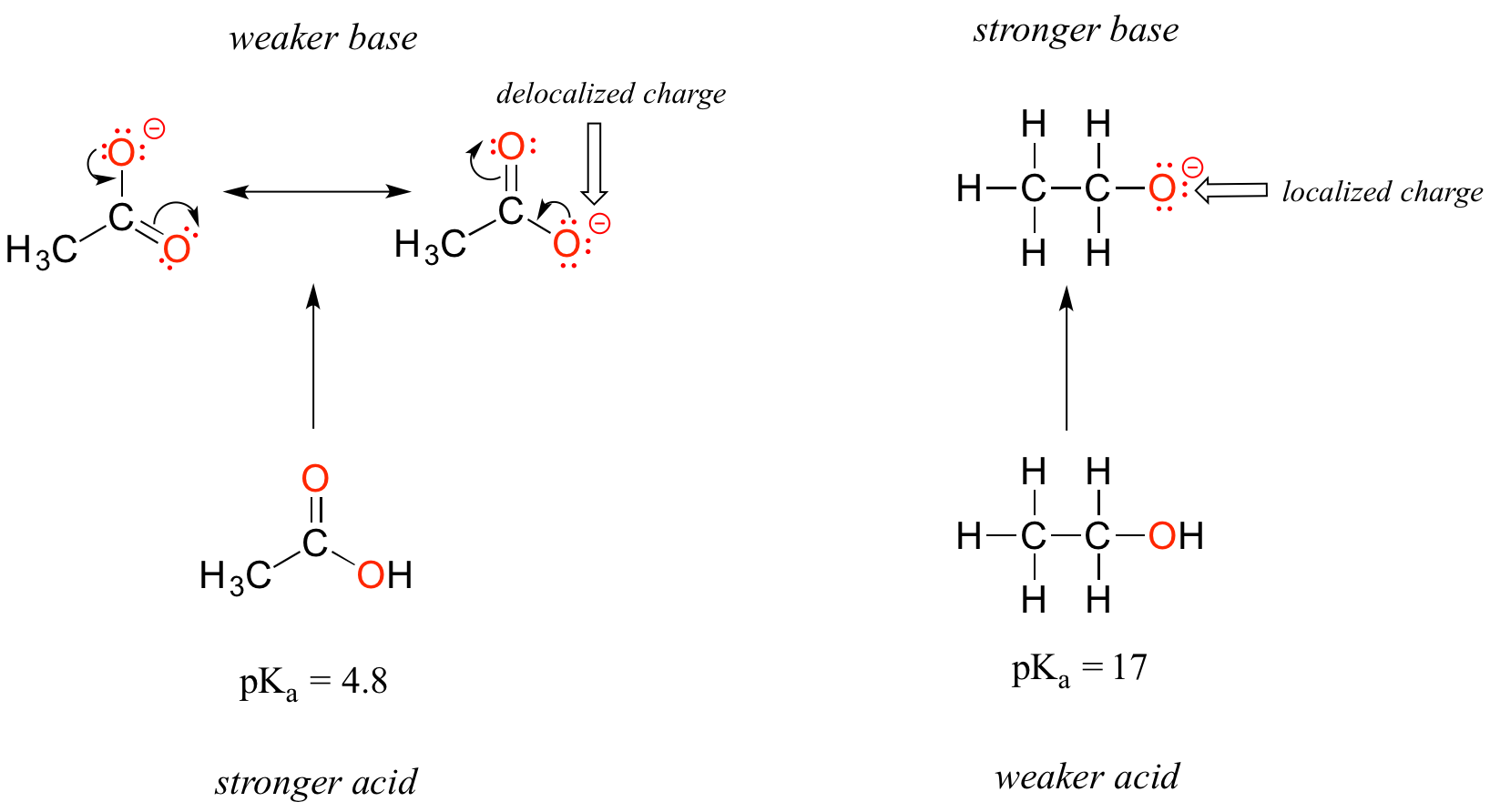
In both species, the negative charge on the conjugate base is located on oxygen, so periodic trends cannot be invoked. For acetic acid, however, there is a key difference: two resonance contributors can be drawn for the conjugate base, and the negative charge can be delocalized (shared) over two oxygen atoms. In the ethoxide ion, by contrast, the negative charge is localized, or ‘locked’ on the single oxygen – it has nowhere else to go. This makes the ethoxide ion much less stable.
Recall the important general statement that we made a little earlier: 'Electrostatic charges, whether positive or negative, are more stable when they are ‘spread out’ than when they are confined to one location.' Now, we are seeing this concept in another context, where a charge is being ‘spread out’ (in other words, delocalized) by resonance, rather than simply by the size of the atom involved.
The delocalization of charge by resonance has a very powerful effect on the reactivity of organic molecules, enough to account for the difference of over 12 pKa units between ethanol and acetic acid (and remember, pKa is a log expression, so we are talking about a fator of 1012 between the Ka values for the two molecules!)
The resonance effect also nicely explains why a nitrogen atom is basic when it is in an amine, but not basic when it is part of an amide group. Recall that in an amide, there is significant double-bond character to the carbon-nitrogen bond, due to a minor but still important resonance contributor in which the nitrogen lone pair is part of a pi bond.
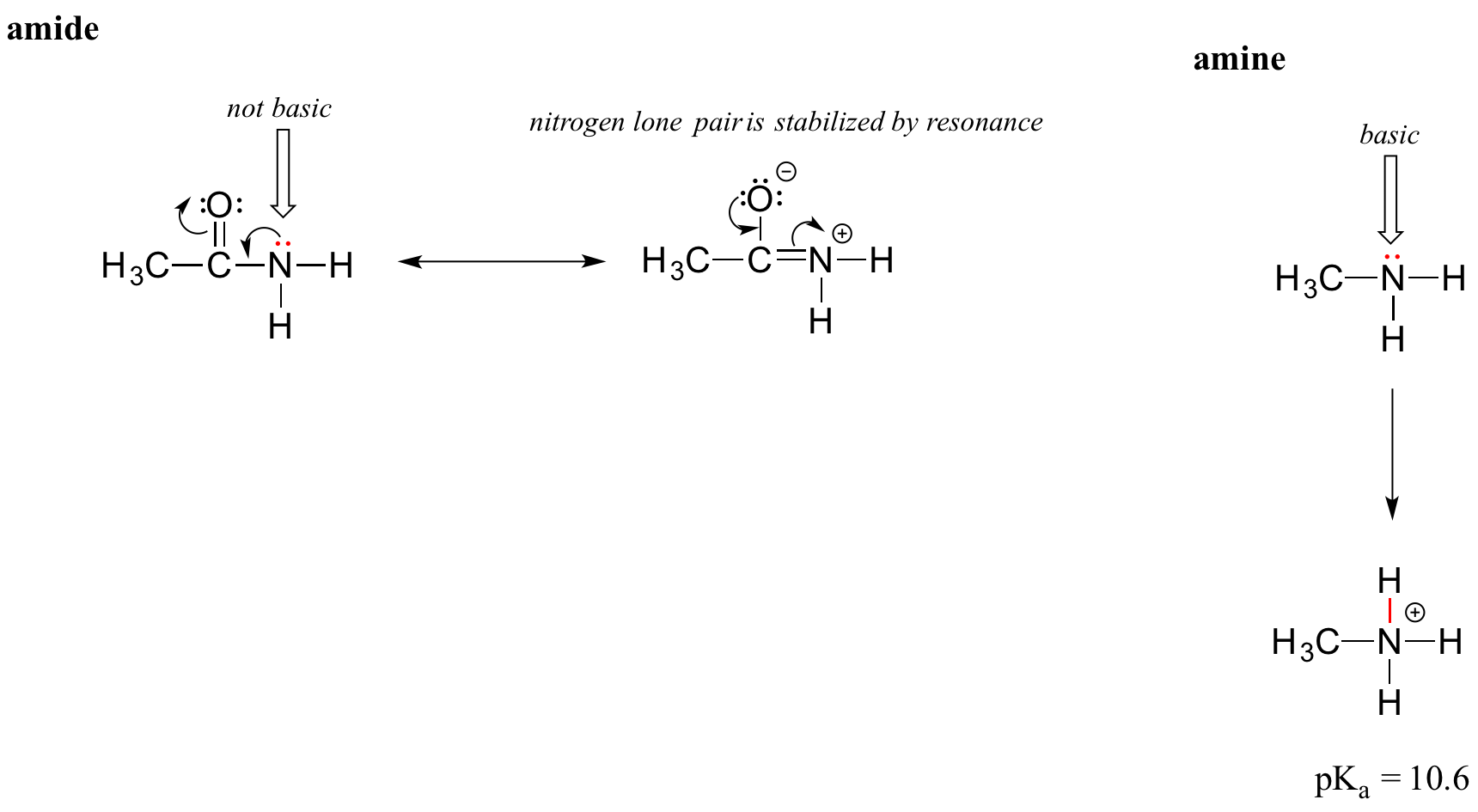
Whereas the lone pair of an amine nitrogen is ‘stuck’ in one place, the lone pair on an amide nitrogen is delocalized by resonance. Notice that in this case, we are extending our central statement to say that electron density – in the form of a lone pair – is stabilized by resonance delocalization, even though there is not a negative charge involved. Here’s another way to think about it: the lone pair on an amide nitrogen is not available for bonding with a proton – these two electrons are too ‘comfortable’ being part of the delocalized pi bonding system. The lone pair on an amine nitrogen, by contrast, is not so comfortable - it is not part of a delocalized pi system, and is available to form a bond with any acidic proton that might be nearby.
If an amide group is protonated, it will be at the oxygen rather than the nitrogen.
Exercise 7.3.1
a) Draw the Lewis structure of nitric acid, HNO3.
b) Nitric acid is a strong acid - it has a pKa of -1.4. Make a structural argument to account for its strength. Your answer should involve the structure of nitrate, the conjugate base of nitric acid.
Exercise 7.3.2
Rank the compounds below from most acidic to least acidic, and explain your reasoning.

Exercise 7.3.3
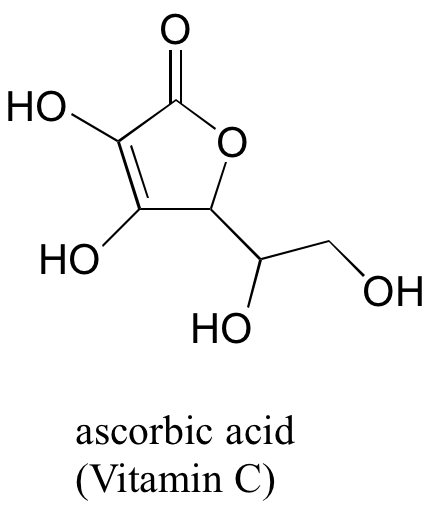
(challenging!) Often it requires some careful thought to predict the most acidic proton on a molecule. Ascorbic acid, also known as Vitamin C, has a pKa of 4.1 - the fact that this is in the range of carboxylic acids suggest to us that the negative charge on the conjugate base can be delocalized by resonance to two oxygen atoms. Which if the four OH protons on the molecule is most acidic? Draw the structure of ascorbate, the conjugate base of ascorbic acid, then draw a second resonance contributor showing how the negative charge is delocalized to a second oxygen atom. Hint - try removing each OH group in turn, then use your resonance drawing skills to figure out whether or not delocalization of charge can occur.
C: Inductive effects
Compare the pKa values of acetic acid and its mono-, di-, and tri-chlorinated derivatives:

The presence of the chlorine atoms clearly increases the acidity of the carboxylic acid group, but the argument here does not have to do with resonance delocalization, because no additional resonance contributors can be drawn for the chlorinated molecules. Rather, the explanation for this phenomenon involves something called the inductive effect. A chlorine atom is more electronegative than a hydrogen, and thus is able to ‘induce’, or ‘pull’ electron density towards itself, away from the carboxylate group. In effect, the chlorine atoms are helping to further spread out the electron density of the conjugate base, which as we know has a stabilizing effect. In this context, the chlorine substituent can be referred to as an electron-withdrawing group. Notice that the pKa-lowering effect of each chlorine atom, while significant, is not as dramatic as the delocalizing resonance effect illustrated by the difference in pKa values between an alcohol and a carboxylic acid. In general, resonance effects are more powerful than inductive effects.
Because the inductive effect depends on electronegativity, fluorine substituents have a more pronounced pKa-lowered effect than chlorine substituents.
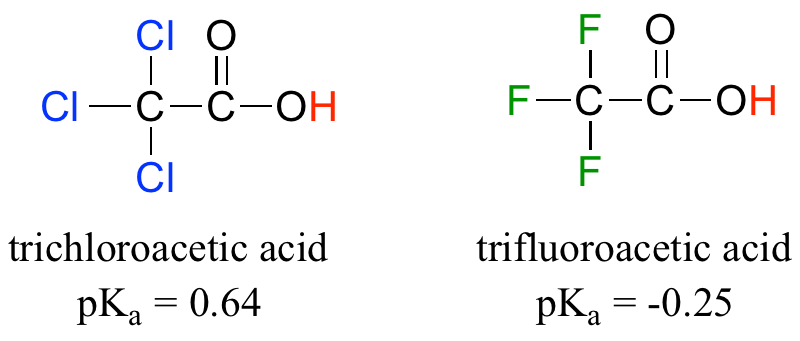
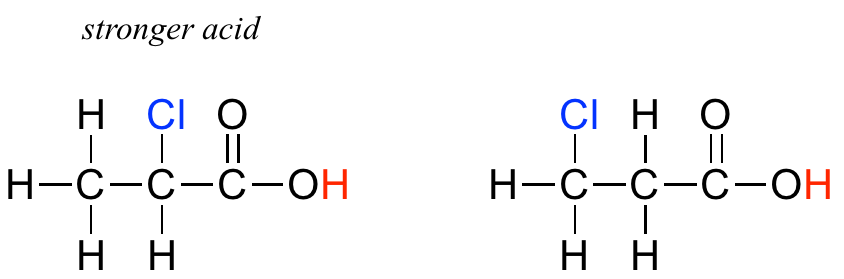
In addition, the inductive takes place through covalent bonds, and its influence decreases markedly with distance – thus a chlorine two carbons away from a carboxylic acid group has a decreased effect compared to a chlorine just one carbon away.
Exercise 7.3.4
Rank the compounds below from most acidic to least acidic, and explain your reasoning.
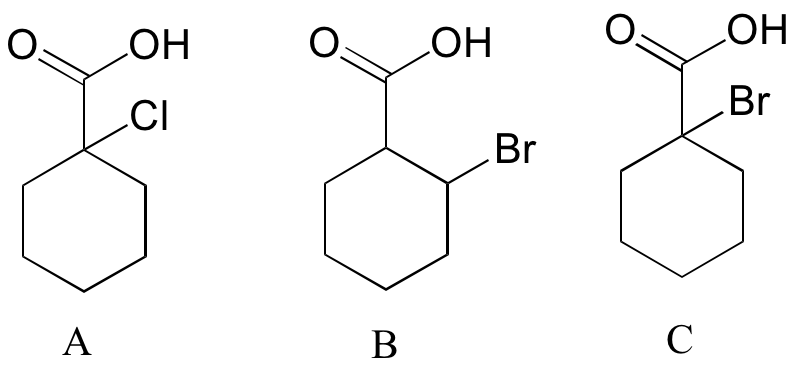
Next section⇒

