5.10: Interpreting Proton NMR Spectra

Objectives

• understand how chemical shift, integration, spin-spin splitting all come together to solve ¹H NMR problems.
• solve unknown ¹H NMR problems given the molecular formula.

This page is devoted to explaining solved ¹H NMR problems to help guide you through different scenarios. The first will be a case in which you know the structure of the product you are synthesizing, but need to prove you did indeed make it. Your strategy should be: 

• Draw your attention to pieces of data that most strongly support your expected structure. A skill necessary for this will be your ability to demonstrate evaluative understanding of the data. In other words, you can look at the data and decide what parts are more important than other parts. 
• Draw you attention to negative results: what peaks might be there if the spectrum matched another possible structure, but is missing. 

Example \(\PageIndex{1}\)

In the laboratory, you performed an esterification to make ethyl acetate. Based on the ¹H NMR spectrum, did you make your desired product? 

Expected Product:  

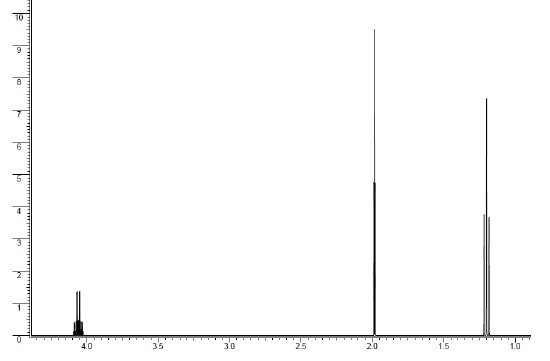
¹H NMR: The ratio of protons is 2:3:3. 

 

 

Solution

Yes, ethyl acetate was synthesized. First, the ratio of protons equals the number of protons in our expected product.

The peak at 1.20 ppm is a triplet that integrates to 3 protons. The integration indicates that the peak corresponds to a methyl group. The splitting pattern of a triplet indicates that there are two neighboring. All of this information together gives the piece -CH₂CH₃. 

The peak at 1.98 ppm is a singlet that integrates to 3 protons. The integration tells us the peak corresponds to a methyl group. The splitting pattern of a singlet indicates that there are no neighbors. The chemical shift is quite far downfield at 1.98 ppm (a methyl group attached to another carbon would be at about 0.9 ppm). Being further downfield means that the methyl group is attached to an electron-withdrawing group, which could be directly to an oxygen or the carbonyl carbon. All of this information together gives the piece -EWG-CH₃. EWG = Electron-Withdrawing Group

The peak at 4.06 ppm is a quartet that integrates to 2 protons. The integration tells us the peak corresponds to a methylene group (-CH₂-). The splitting pattern of a quartent indicates that there are 3 neighbors. The chemical shift is quite far downfield at 4.06 ppm (a methylene group attached to another carbon would be at about 1.2 ppm). Being the furthest downfield, the methylene group needs to be attached to the electron-withdrawing group that will be the most deshielding for the protons (Chemical Shift information). This is the proton must be directly attached to the oxygen. All of this information together gives the piece -O-CH₂CH₃, which means the methyl group at 1.98 ppm is directly attached to the carbonyl carbon. 

From this analysis, it can be concluded that yes, ethyl acetate was synthesized as expected. 

Next, we will look at a ¹H NMR spectrum of an unknown and determine its structure. 

Example \(\PageIndex{2}\)

Using the chemical formula and ¹H NMR spectrum, determine the structure of your unknown molecule. 

Chemical Formula: C₅H₉ClO

Unknown molecule ¹H NMR spectrum: The ratio of protons is 2:2:2:3.

 

Solution

Unknown molecule: 

First, if the molecular formula is known, then start by calculating the degree of unsaturation (DU), which will tell how many double bond, triple bond, or rings are present in the molecule. A double bond is a DU = 1. A ring is a DU = 1. A triple bond is a DU = 2. The degree of unsaturation for C₅H₉ClO is 1. Therefore, the molecule either contains a ring or a double bond. 

The peak at 1.05 ppm is a triplet that integrates to 3 protons. The integration indicates that the peak corresponds to a methyl group. The splitting pattern of a triplet indicates that there are two neighboring. All of this information together gives the piece -CH₂CH₃. 

The peak at 2.40 ppm is a quartet that integrates to 2 protons. The integration tells us the peak corresponds to a methylene group. The splitting pattern of a quartet indicates that there are 3 neighboring protons. The chemical shift is quite far downfield at 2.40 ppm (a methylene group attached to another carbon would be at about 1.2 ppm). Being further downfield means that the methylene group is attached to an electron-withdrawing group, which could be directly to the chlorine or carbonyl carbon. All of this information together gives the piece -EWG-CH₂CH₃. EWG = Electron-Withdrawing Group

The peak at 2.90 ppm is a triplet that integrates to 2 protons. The integration tells us the peak corresponds to a methylene group. The splitting pattern of a triplet indicates that there are 2 neighboring protons. The chemical shift is quite far downfield at 2.90 ppm. Being further downfield means that the methylene group is attached to an electron-withdrawing group, which could be directly to the chlorine or carbonyl carbon. All of this information together gives the piece -EWG-CH₂CH₂-.

The peak at 3.77 ppm is a triplet that integrates to 2 protons. The integration tells us the peak corresponds to a methylene group. The splitting pattern of a triplet indicates that there are 2 neighbors. The chemical shift is quite far downfield at 3.77 ppm. Being the furthest downfield, the methylene group needs to be attached to the electron-withdrawing group that will be the most deshielding for the protons (Chemical Shift information). This is the proton must be directly attached to the chlorine. All of this information together gives the piece Cl-CH₂CH₂-, which means the methylene groups at 2.40 and 2.90 ppm are directly attached to the carbonyl carbon, since the chlorine only makes one bond. 

All of this information yields the unknown molecule structure to be .

In the example just discussed, the number of hydrogens in the spectrum was equal the number of hydrogens in the molecular formula. What if this is not the case? Symmetry in a molecule can complicate your ability to determine a structure because the ¹H NMR spectrum seems more simple than expected.  

Example \(\PageIndex{3}\)

Using the chemical formula and ¹H NMR, determine the structure of the unknown molecule. 

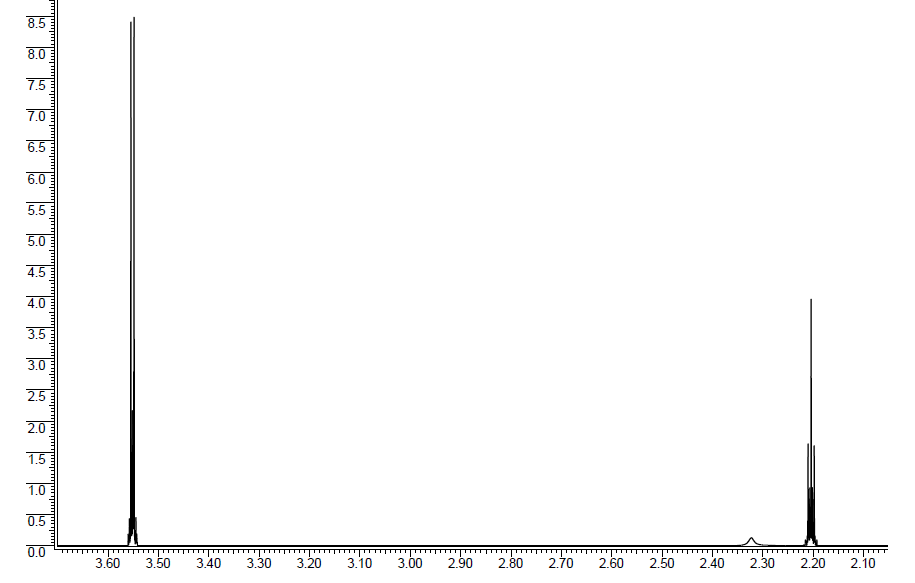
Molecular formula: C₆H₇N

Unknown molecule ¹H NMR spectrum: The ratio is 1:1:2.

Solution

Unknown molecule: .

Thus far, we have not needed to use the J-coupling constants from the splitting patterns, because the constants would have all been very similar of about 7 Hz. However, they can be very useful in determining your final product and ruling out other possibilities. 

Example \(\PageIndex{4}\)

Using the chemical formula and the ¹H NMR spectrum, determine the structure of the unknown molecule. 

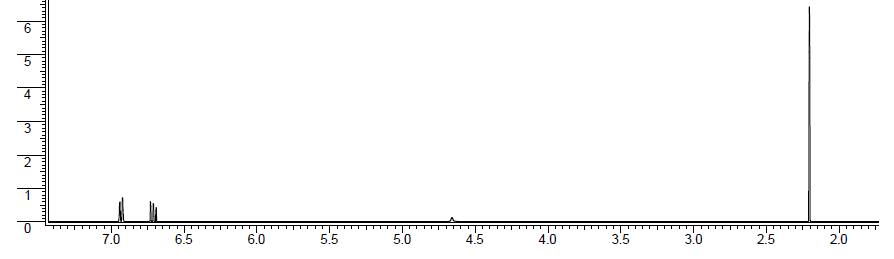
Molecular formula: C₈H₁₀O. 

Unknown molecule ¹H NMR spectrum: The proton ratio is 2:1:1:6. The coupling constant for the doublet (6.93 ppm) and triplet (6.71 ppm) is 8 Hz.

Solution

DU = 4. Anytime there is a DU of at least 4, it is often an aromatic ring. Each double bond is 1 DU and the ring is 1 DU, so 3(1) + 1 = 4.

To double check this, look to see if there are any protons in the aromatic proton region (6.5 ppm - 8 ppm). This spectrum does in fact have aromatic protons, so there must be an aromatic ring. There is a total of 3 protons in the aromatic region, which means that there are three hydrogens coming of the aromatic ring and three groups coming off the aromatic ring. The coupling constant of 8 Hz indicates that the aromatic protons are ortho to one anther. The piece from this information is . 

For the groups, since there are only two types of aromatic protons, this means that the groups ortho to the hydrogens must be the same. 

The peak at 4.66 ppm is broad and small and integrates to one proton. Broad peaks typically are from exchangeable protons attached to oxygen or nitrogen. Since our molecular formula contains an O, this must be a hydroxyl group (-OH).

The singlet at 2.20 ppm integrates to 6 protons. The most common way to have 6 equivalent protons is that there are two methyl groups with no neighbors. Two methyl groups would be two of the same group and therefore are the groups ortho to the protons on the aromatic ring.  

All of this information yields the unknown molecule structure to be  .

The final example brings in a more complex splitting pattern. 

Example \(\PageIndex{5}\)

Using the chemical formula and the ¹H NMR spectrum, determine the structure of the unknown molecule. 

Molecular formula: C₄H₆O. 

Unknown molecule ¹H NMR spectrum: The proton ratio is 1:1:1:1:2. The coupling constant for the doublet of doublet of triplets (5.93 ppm) has three coupling constants which are 17 Hz, 10 Hz, and 7 Hz. and triplet (6.71 ppm) is 8 Hz. The doublet of doublets at 5.20 ppm has coupling constants of 10 Hz and 2 Hz and the doublet of doublets at 5.10 ppm has coupling constants of 17 Hz and 2 Hz. The doublet at 3.12 ppm has a coupling constant of 7 Hz. 

Solution

DU = 2. Therefore, there is either a double bond or a ring. If we look at chemical shifts, there are peaks in the double bond region, so the molecule has at least one double bond. 

Another thing to note is that the ratio of protons equals our total number of protons of 6. Therefore, all the protons are accounted for and there is not integration of 3, so this molecule has NO methyl groups. 

The peak out at 10 ppm is an aldehyde proton. Very few peaks show up that far downfield and using the chemical shift table, it indicates that it is an aldehydic proton. An aldehyde contains a carbonyl (C=O), which is our second degree of unsaturation. 

The peak at 3.12 ppm is a methylene (-CH₂-) group, since the integration is 2. It is quite far downfield, so it must be near an electron-withdrawing group. So far, there is an aldehyde, which would be an "end" to the molecule much like a methyl group. The fragment piece could be .

This brings us to the double bond region. In total, there are three double bond protons, which means we have a terminal double bond. There is only one way to have a double bond with three protons, but let's consider the splitting. If we combine the double bond with the fragment we have, then our molecule would be . H_A is a doublet of doublets. It is split by cis coupling to H_c of 10 Hz and geminal coupling to H_B of 2 Hz, which yields a doublet of doublets. H_B is a doublet of doublets. It is split by trans coupling to H_c of 17 Hz and geminal coupling to H_A of 2 Hz, which yields a doublet of doublets. The doublet of doublet of triplets is H_c. As we just discussed, it couples through cis bonding to H_A (10 Hz) and trans to H_B (17 Hz). The triplet comes from regular 3-bond coupling to the methylene group, which is J = 7 Hz.  

All of this information yields the unknown molecule structure to be  .

The next section will have problems for you to solve.