11.3: Reduction Reactions
- Page ID
- 168839
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The enantioselective reduction of C=X double bonds (X = O, NR, C) to C-XH single bonds plays a major role in asymmetric synthesis.
Reduction of Ketones
The enantioselective reduction of ketones represents an atom-economical approach towards optically active alcohols. The biocatalytic reduction of ketones is based on the use of an alcohol dehydrogenase (ADH) as a catalyst, and a cofactor as a reducing agent. For example, ADH from Leifsonia sp. catalyses the reduction of substituted acetophenone to give secondary alcohols with high enantioselectivity (Scheme \(\PageIndex{1}\)). In this process, 2-propanol acts as a reducing agent oxidizing into acetone.

The keto group of 2,5-diketo ester can be selectively reduced with excellent regio- and enantioselectivity using E. coli cells with overexpressed ADH from Lactobacillus brevis (Scheme \(\PageIndex{2}\)). In this process 2-propanol acts as a reducing agent oxidizing into acetone.
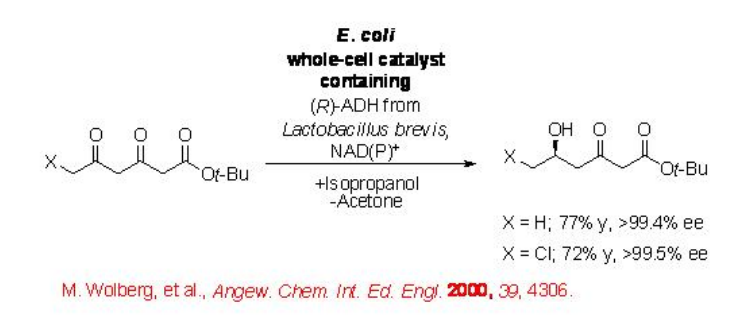
The reduction of a wide range of aliphatic and aromatic ketones can be accomplished employing R. ruber ADH to give the corresponding alcohols with excellent enantioselectivity in 2-propanol (Scheme \(\PageIndex{7}\)).
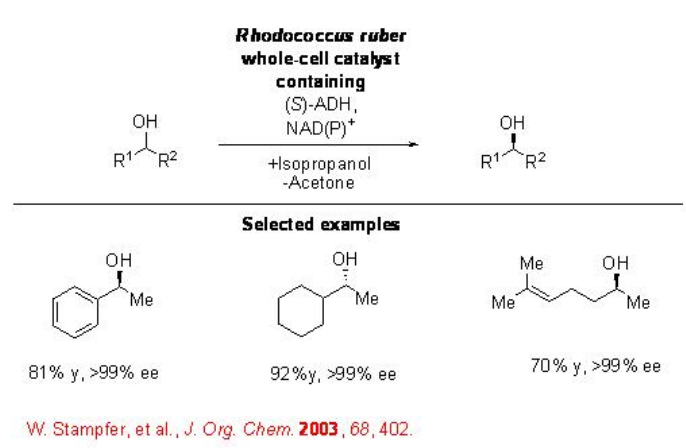
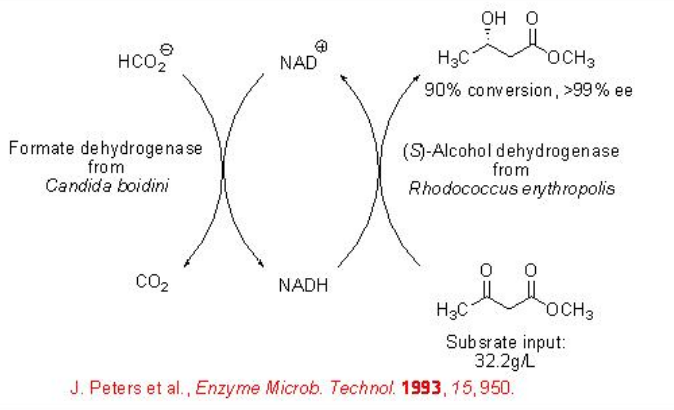
Whereas formate dehydrogenase (FDH) from C. boidinii catalyzes selectively the reduction of keto group of β -keto esters with high enantioselectivity. In this reaction, formate is oxidized into carbon dioxide (Scheme \(\PageIndex{4}\)).
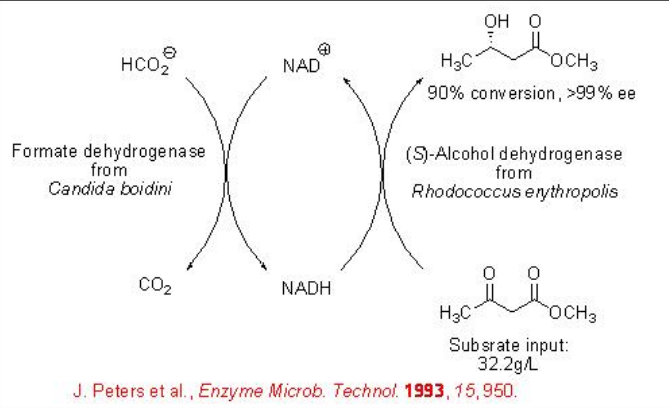
The FDH-based whole-cell can be used for the reduction of ethyl 4-chloro-3-oxobutanoate with 99% ee (Scheme \(\PageIndex{5}\)).
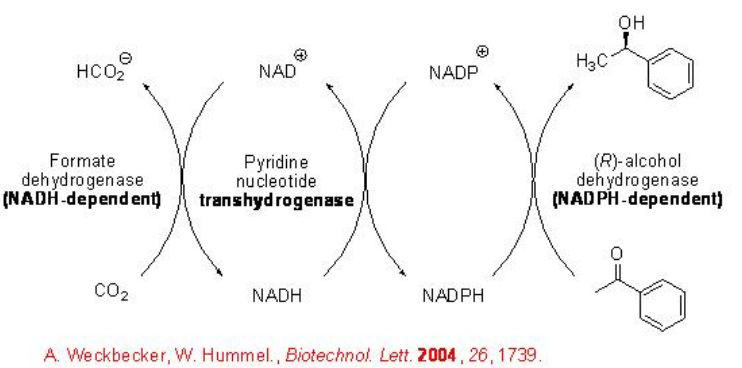
The use of FDH from C. boidinii has limitation due to its inability to regenerate NADP+. This has been overcome by expanding the application range of FDH-based cofactor regeneration to NADP+ -dependent ADHs (Scheme \(\PageIndex{6}\)). This involves the integration of an additional enzymatic step within the cofactor-regeneration cycle that is exemplified in the reduction of acetophenone to (R)-phenylethanol. In this process, the pyridine nucleotide transhydrogenase (PNT)-catalyzes regeneration of NADPH from NADP+ under consumption of NADH forming NAD+.
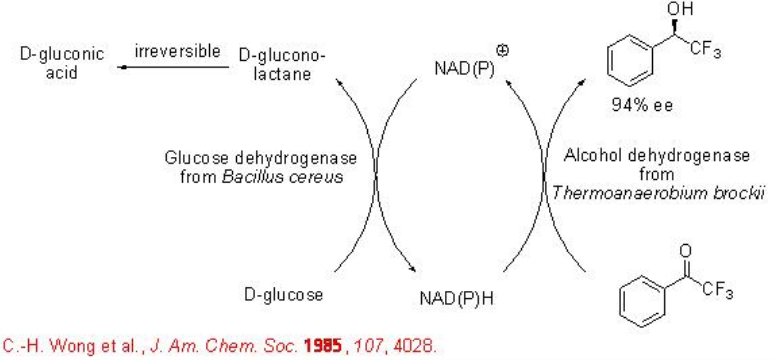
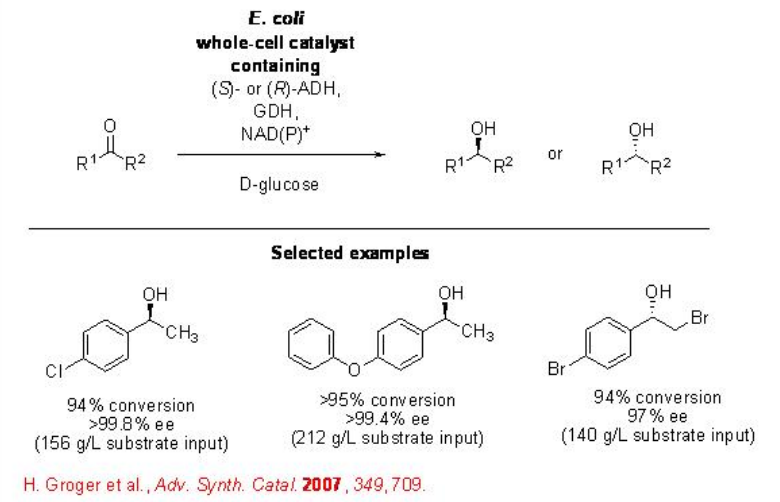
Further, for recycling the cofactor NAD(P)H, the use of a glucose dehydrogenase (GDH) has been demonstrated. In this system, D-glucose is oxidized to D-gluconolactone, while the oxidized cofactor NAD(P+) is reduced to NAD(P)H. Since D-gluconolactone is then hydrolyzed into D-gluconic acid, the reaction is irreversible shifting the whole process towards the desired alcohol product formation. This GDH coupled cofactor-regeneration process has been used for the reduction of ketone to alcohol with high enantioselectivity (Scheme \(\PageIndex{7}\)).
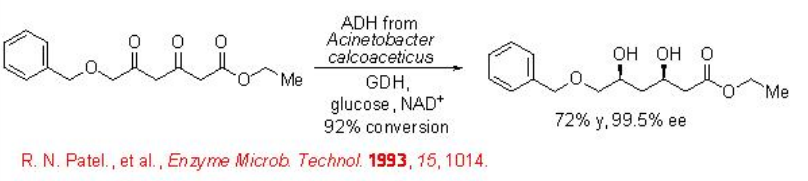
This principle has been recently used for the reduction of ethyl 6-benzyloxy-3,5-dioxohexanoate to afford ethyl (3 R,5 S )-6-benzyloxy-3,5-dihydroxyhexanoate with 99% ee employing ADH from Acinetobacter calcoaceticus in combination with a GDH and glucose (Scheme \(\PageIndex{8}\)).
Reduction of Ketones
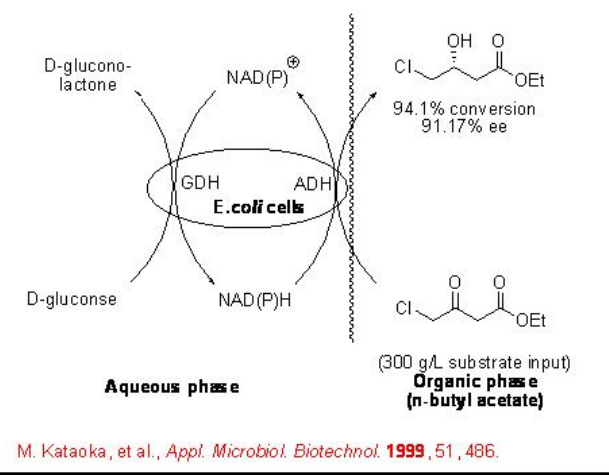
Recombinant whole-cell catalytic system having E. coli , co-expressing both the ADH from S. salmonicolor and the GDH from B. megaterium , has been developed for the asymmetric reduction of 4-chloro-3-oxobutanoate in a mixture of n -butyl acetate/water (Scheme \(\PageIndex{9}\)). It is an elegant approach toward tailor-made biocatalysts containing both of the desired enzymes, ADH and GDH, in overexpressed form (Scheme \(\PageIndex{9}\)).
The application of recombinant whole-cell biocatalytic system has been further demonstrated in pure aqueous media without the need of addition of external amount of cofactor (Scheme \(\PageIndex{10}\)). This method is economical and simple, and finds applications for the reduction of a wide range of ketones (Scheme \(\PageIndex{10}\)).
Reductive Amination of α -Keto Acids
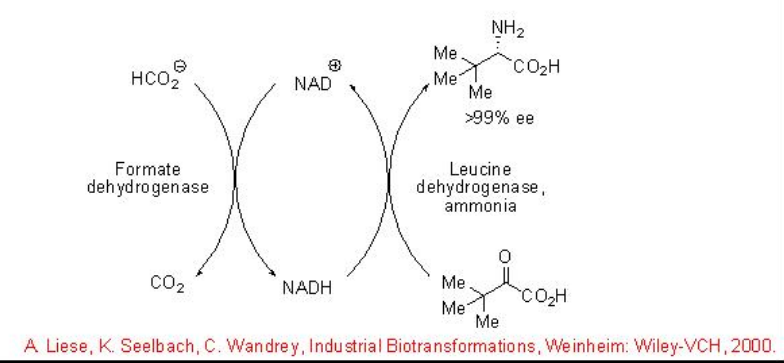
Enzyme catalyzed asymmetric reductive amination of α -keto acids represents a straightforward method to access optically active α -amino acids. For example, L- tert- leucine, which serves as building block for the pharmaceutical industry, is obtained with high conversion and enantioselectivity using a leucine dehydrogenase for the reductive amination and an FDH from C.boidinii (Scheme \(\PageIndex{11}\)). The latter is required for an in situ recycling of the cofactor NADH.
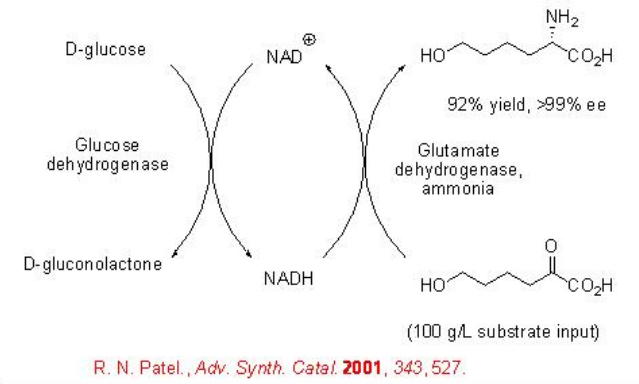
Similarly, the synthesis of L-6-hydroxynorleucine can be accomplished from α -keto acid with complete conversion and >99% enantioselectivity (Scheme \(\PageIndex{12}\)). In this reaction, a beef liver glutamate dehydrogenase has been used as L-amino acid dehydrogenase and a GDH from B. megaterium has been used for the cofactor regeneration.
However, the need for the addition of expensive cofactor NAD+ as well as the isolation and cost of the enzymes make these approaches are limited. Thus, efforts have been made to address these aspects by employing a whole-cell catalyst, having both an amino acid dehydrogenase and FDH in overexpressed form. For example, the synthesis of L-allysine ethylene acetal has been shown using a whole-cell catalyst, Pichia pastoris cells having a phenylalanine dehydrogenase from Thermoactinomyces intermedius and an FDH from P. pastoris (Scheme \(\PageIndex{13}\)).
Reduction of Activated Carbon-Carbon Double Bonds
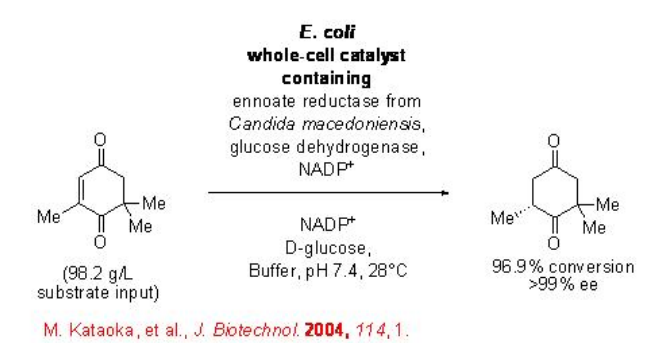
The reduction of carbon-carbon double bonds using the biocatalytic systems has high potential in organic chemistry. However, this process is less explored compared to the C=O reduction of ketones and keto esters. The reduction of the carbon-carbon double bond in ketoisophorone has been accomplished using whole-cell catalyst overexpressing an enolate reductase from Candida macedoniensis and a GDH (Scheme \(\PageIndex{13}\)). This study can be regarded as one of the pioneering works in the reduction of carbon-carbon double bonds using biocatalytic systems.
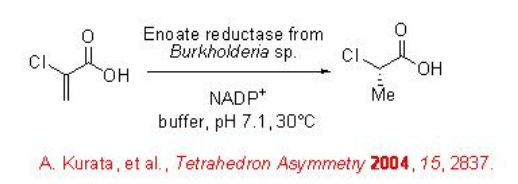
α,β -Unsaturated carboxylic acids can also be used as substrates. For example, α -chloroacrylic acid can be converted into α -chloropropionate using an enolate reductase from Burkholderia sp ., in high enantioselectivity (Scheme \(\PageIndex{14}\)).
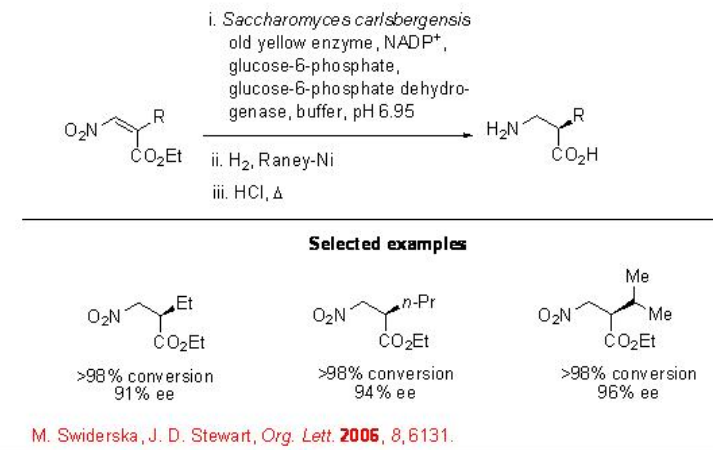
Besides, enone and α,β -unsaturated carboxylic acid, nitroalkanes are also suitable substrates for enoate reductase. For example, the reduction of carbon-carbon double bond in Z -nitroalkenes proceed reaction to give 2-substituted 3-nitropropanoates with high conversion and in most cases with high enantioselectivity (Scheme \(\PageIndex{15}\)).
Transamination\(\PageIndex{1}\)
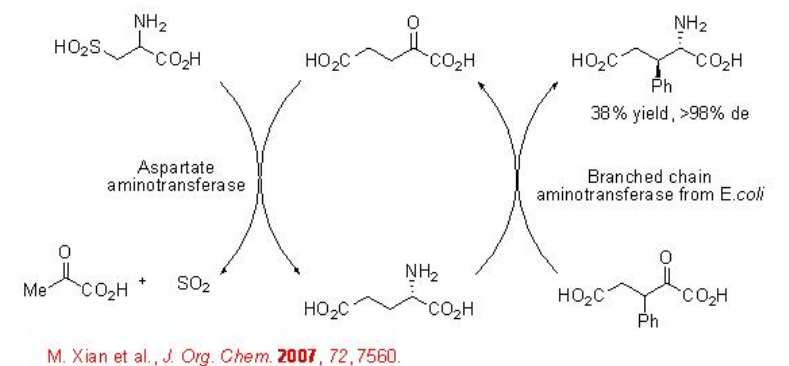
Depending on the nature of the transaminase, α -keto acids and ketones proceed reaction to give α-amino acids and amines with a stereogenic center in α -position, respectively. For example, a coupling of the transaminase process with an irreversible aspartate aminotransferase-catalyzed transamination process using cysteine sulfinic acid as an amino donor has been used for the synthesis of various types of non-natural 3- or 4-substituted glutamic acid analogues (Scheme \(\PageIndex{16}\)).
Furthermore, the highly efficient synthesis (S)-methoxyisopropylamine has been accomplished using a recombinant whole-cell catalyst overexpressing a transaminase. A key feature in this process is the high substrate concentration and the desired target molecule can be obtained with excellent enantioselectivity (Scheme \(\PageIndex{17}\)).



