14.2: Electrophilic Addition to Alkenes
- Page ID
- 106379
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Addition of \(HBr\) to alkenes
The simplest type of electrophilic reaction to visualize is the addition of a haloacid such as \(HBr\) to an isolated alkene. It is not a biological reaction, but nonetheless can serve as a convenient model to introduce some of the most important ideas about electrophilic reactions.
Electrophilic addition of \(HBr\) to an alkene:
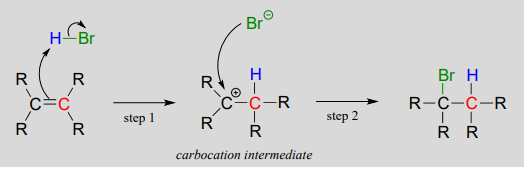
Step 1 is an acid-base reaction: the \(\pi \) electrons of the alkene act as a base and extract the acidic proton of \(HBr\). This leaves one of the carbons with a new bond to hydrogen, and the other with an incomplete octet and a positive formal charge. In step 2, the nucleophilic bromide anion attacks the electrophilic carbocation to form a new carbon-bromine bond. Overall, the \(HBr\) molecule - in the form of a proton and a bromide anion - has been added to the double bond.
To understand how \(\pi \)-bonded electrons in an alkene could be basic, let's first review the bonding picture for alkenes. Recall (section 2.1) that the both of the carbons in an alkene group are \(sp^2\) hybridized, meaning that each carbon has three \(sp^2\) hybrid orbitals extending out in the same plane at \(180^{\circ}\) angles (trigonal planar geometry), and a single, unhybridized \(p\) orbital oriented perpendicular to that plane - one lobe above the plane, one lobe below.
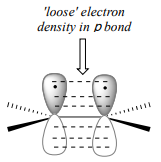
The unhybridized \(p\) orbitals on the two alkene carbons overlap, in a side-by-side fashion, to form the \(pi \) bond, which extends above and below the plane formed by the \(s\) bonds. two electrons shared in this π bond are farther away from the carbon nuclei than the electrons in the carbon-carbon \(s\) bond, and thus are more accessible to the acidic proton. In addition, recall that molecular orbital (MO) theory tells us that \(p\) orbitals are higher in energy than s orbitals (section 2.2). As a consequence, it is easier to break the \(p\) bond of an alkene than it is to break the \(s\) bond: the \(p\) bond is more reactive.
As the \(HBr\) molecule approaches the alkene, a new \(s\) bond is formed between one of the alkene carbons and the electron-poor proton from \(HBr\). The carbon, which was \(sp^2\) hybridized when it was part of the alkene, is now \(sp^3\) hybridized. The other alkene carbon is still \(sp^2\) hybridized, but it now bears a positive formal charge because it has only three bonds, and its \(p\) orbital is empty. But it won't stay empty for long: a carbocation is a very reactive, unstable intermediate. The bromide ion will rapidly act as a nucleophile, filling the orbital with a pair of electrons, and now with four \(s\) bonds the carbon is \(sp^3\)-hybridized.
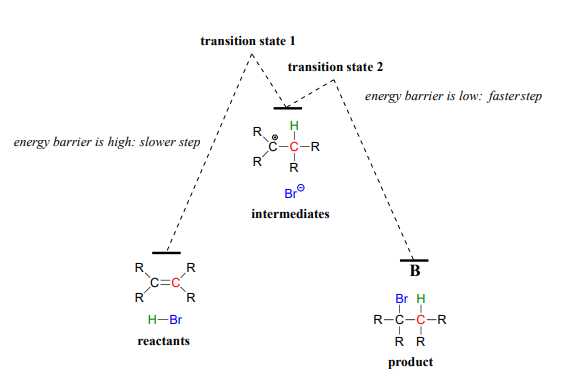
The first step in the electrophilic addition reaction is much slower than the second step, because the intermediate carbocation species is higher in energy than either the reactants or the products, and as a result the energy barrier for the first step is also higher than for the second step. The slower first step is the rate-determining step: a change in the rate of the slow step will effect the rate of the overall reaction, while a change in the rate of the fast step will not.
It is important to recognize the inherent difference between an electrophilic addition to an alkene and a conjugate addition to an alkene in the \(\square \square \square\) position, the latter of which we studied earlier in section 13.4. In both reactions, a proton and a nucleophile add to the double bond of an alkene. In a conjugate addition, the nucleophilic attack takes place first, resulting in a negatively charged intermediate (an enolate). Protonation is the second step. Also, of course, the alkene must be conjugated to a carbonyl or imine.
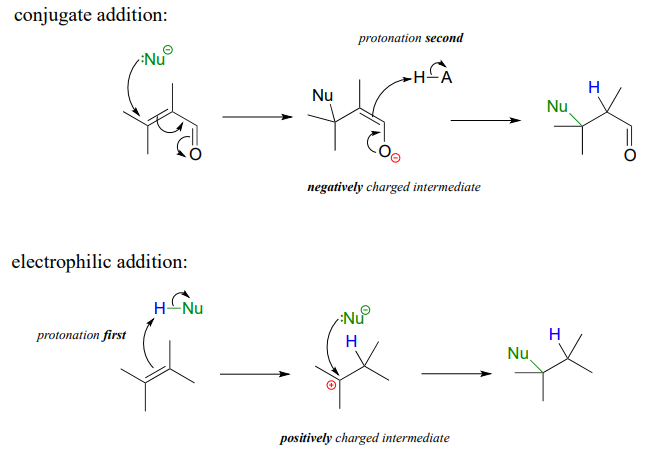
In an electrophilic addition, proton abstraction occurs first, generating a positively-charged intermediate. Nucleophilic attack is the second step. No conjugated carbonyl or imine group is required: in fact a nearby carbonyl group would actually slow down a hypothetical electrophilic addition reaction down because a carbonyl is an electron withdrawing, carbocation-destabilized group.
The stereochemistry of electrophilic addition
Depending on the structure of the starting alkene, electrophilic addition has the potential to create two new chiral centers. Addition of \(HBr\) to an alkene is not stereoselective: the reaction results in racemization at both of the alkene carbons. Consider the addition of \(HBr\) to cis-3,4-dimethyl-3-hexene. The initial proton abstraction step creates a new chiral center, and because the acidic proton could be added to either side of the planar alkene carbon with equal probability, the center could have either \(S\) or \(R\) configuration.
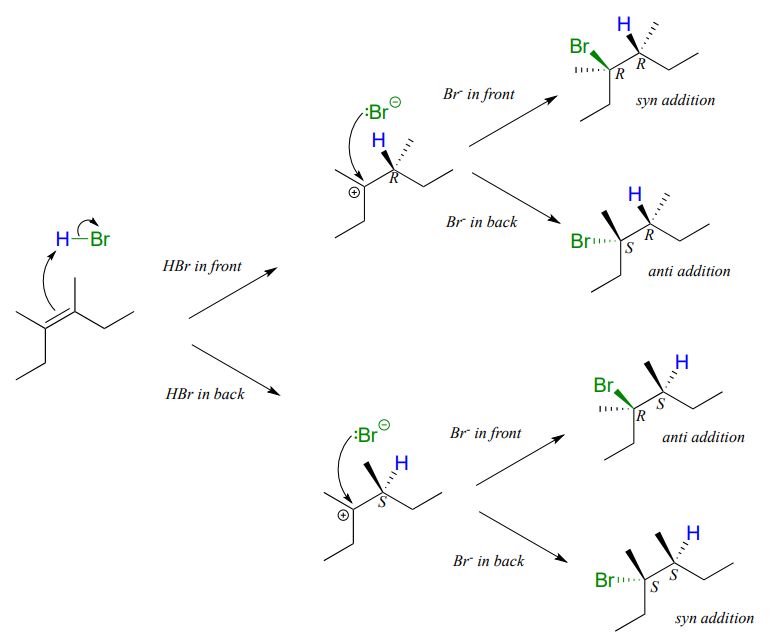
Likewise, in the second step the nucleophilic bromide ion could attack from either side of the planar carbocation, leading to an equal mixture of \(S\) and \(R\) configuration at that carbon as well. Therefore, we expect the product mixture to consist of equal amounts of four different stereoisomers.
Predict the product(s) of electrophilic addition of \(HBr\) to the following alkenes. Draw all possible stereoisomers that could form, and take care not to draw identical structures twice.
- trans-2-butene
- cis-3-hexene
- cyclopentene
The regiochemistry of electrophilic addition
In many cases of electrophilic addition to an alkene, regiochemistry comes into play: the reaction can result in the formation of two different constitutional isomers. Consider the electrophilic addition of \(HBr\) to 2-methylpropene:
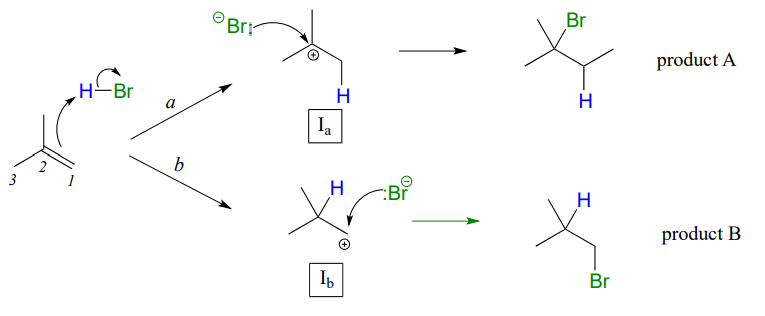
Note that carbon #1 and carbon #2 in the starting alkene are not the same - carbon #2 is bonded to two methyl groups, and carbon #1 to two hydrogen atoms. The initial protonation step could therefore go two different ways, resulting in two different carbocation intermediates. Notice how pathway 'a' gives a tertiary carbocation intermediate (\(I_a\)), while pathway 'b' gives a primary carbocation intermediate (\(I_b\)) We know from section 8.5 that the tertiary carbocation \(I_a\) is lower in energy. Consequently, the transition state \(TS(a)\) leading to \(I_a\) is lower in energy than \(TS(b)\), meaning that \(I_a\) forms faster than \(I_b\).
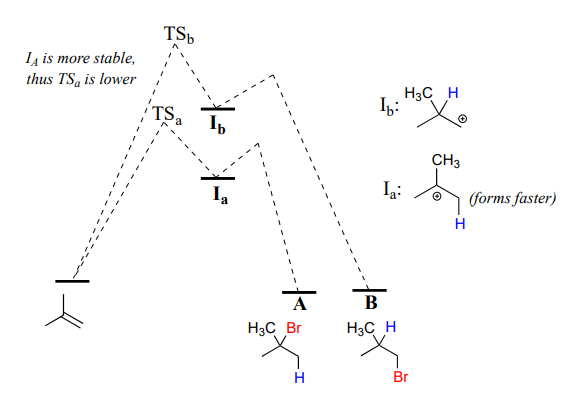
Because the protonation step is the rate determining step for the reaction, tertiary alkyl bromide A will form faster than the primary alkyl bromide B, and thus A will be the predominant product of the reaction. The electrophilic addition of \(HBr\) to 2-methylpropene is regioselective: more than one constitutional isomer can potentially form, but one isomer is favored over the other. It is generally observed that in electrophilic addition of haloacids to alkenes, the more substituted carbon is the one that ends up bonded to the heteroatom of the acid, while the less substituted carbon is protonated. This 'rule of thumb' is known as Markovnikov's rule, after the Russian chemist Vladimir Markovnikov who proposed it in 1869.
While it is useful in many cases, Markovikov's rule does not apply to all electrophilic addition reactions. It is better to use a more general principle:
When an asymmetrical alkene undergoes electrophilic addition, the product that predominates is the one that results from the more stable of the two possible carbocation intermediates.
How is this different from Markovnikov's original rule? Consider the following hypothetical reaction, in which the starting alkene incorporates two trifluoromethyl substituents:
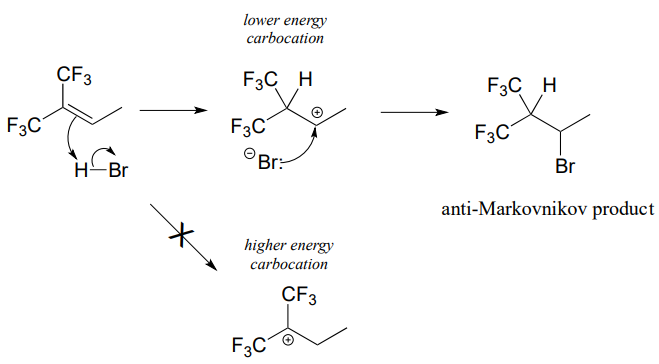
Now when \(HBr\) is added, it is the less substituted carbocation that forms faster in the rate-determining protonation step, because in this intermediate the carbon bearing the positive charge is located further away from the electron-withdrawing, cation-destabilizing fluorines. As a result, the predominant product is the secondary rather than the tertiary bromoalkane. This is referred to as an anti-Markovnikov addition product, because it 'breaks' Markovnikov's rule.
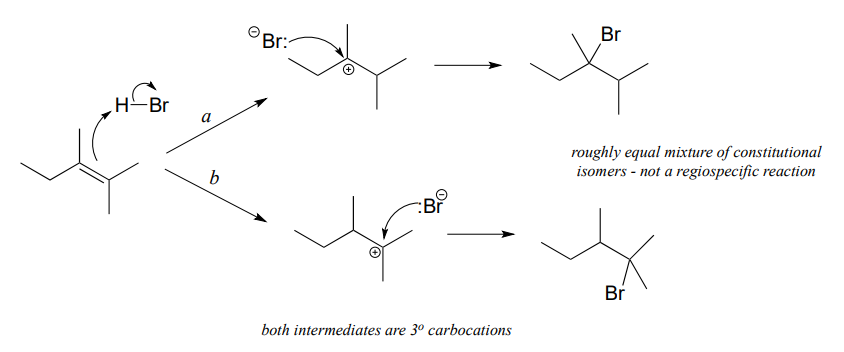
If the two possible carbocation intermediates in an electrophilic addition reaction are of similar stability, the product will be a mixture of constitutional isomers.
Electrophilic addition of water and alcohol
The (non-biochemical) addition of water to an alkene is very similar mechanistically to the addition of a haloacid such as \(HBr\) or \(HCl\), and the same stereochemical and regiochemical principles apply. A catalytic amount of a strong acid such as phosphoric or sulfuric acid is required, so that the acidic species in solution is actually \(H_3O^+\). Note that \(H_3O^+\) is regenerated in the course of the reaction.

Figure 14.2.10
If an alkene is treated with methanol and a catalytic amount of strong acid, the result is an ether:

Figure 14.2.11
Draw a mechanism for the ether-forming reaction above.
Addition to conjugated alkenes
Electrophilic addition to conjugated alkenes presents additional regiochemical possibilities, due to resonance delocalization of the allylic carbocation intermediate. Addition of one molar equivalent of \(HBr\) to 1,3-butadiene, for example, leads to a mixture of three products, two of which are a pair of enantiomers due to the creation of a chiral center at carbon #2.

Figure 14.2.12
Explain why 4-bromo-1-butene is not a significant product of the reaction above.
Predict the major product(s) of the following reactions. Draw all possible stereoisomers, and take care not to draw the same structure twice.



- Hint - are the double bonds in an aromatic ring likely to undergo electrophilic addition?

Biochemical electrophilic addition reactions
Myrcene is an isoprenoid compound synthesized by many different kinds of plants and used in the preparation of perfumes. Recently an enzymatic pathway for the degradation of myrcene has been identified in bacteria (J. Biol. Chem 2010, 285, 30436). The first step of this pathway is electrophilic addition of water to a conjugated alkene system.

Figure 14.2.13
Draw a mechanism for the above reaction, showing two resonance contributors of the carbocation intermediate. How would you characterize the intermediate?
Although the hydration of myrcene above looks very familiar, many enzyme-catalyzed electrophilic addition reactions differ from what we have seen so far, in that the electron-poor species attacked by the p-bonded electrons in the initial step is a carbocation rather than an acidic proton:

Figure 14.2.14
\(\square\)-terpineol, a major component in the sap of pine trees, is formed in an electrophilic addition reaction. The first thing that happens (which we will refer to below as 'step a', in order to keep the step numbering consistent what the addition mechanisms we have seen so far) is departure of a pyrophosphate leaving group, forming an allylic carbocation electrophile.

Figure 14.2.15
The actual electrophilic addition stage of the reaction begins with step 1, as the π electrons an alkene are drawn toward one of the two carbons that share the positive charge, effectively closing a six-membered ring. A water molecule then attacks the second carbocation intermediate (step 2), which completes the addition process.
Notice something important about the regiochemical course of the reaction: step 1 results in the formation of a six-membered ring and a tertiary carbocation. As we have stressed before, biochemical reactions tend to follow energetically favorable mechanistic pathways.
An alternate regiochemical course to step 1 shown above could result in a seven-membered ring and a secondary carbocation, a much less energetically favorable intermediate in terms of both carbocation stability and ring size. Draw a mechanism for this hypothetical alternate reaction, and show the product that would result after the addition of water in a hypothetical 'step 2'.



