21.5: Application of the MO Method to 1,3-Butadiene
- Page ID
- 22314
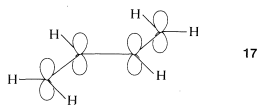
To treat the \(\pi\)-electron system of 1,3-butadiene by simple MO theory, we combine the four \(p\) carbon orbitals of an atomic-orbital model, such as \(17\), to obtain four molecular orbitals:

We can estimate a stabilization energy for butadiene from heats of hydrogenation, and it is useful to compare the values obtained with the calculated delocalization energy. Thus the heat of hydrogenation of 1,3-butadiene is \(57.1 \: \text{kcal}\), whereas that of ethene is \(32.8 \: \text{kcal}\) and of propene \(30.1 \: \text{kcal}\). If ethene is used as the model alkene, the stabilization energy of 1,3-butadiene is \(\left( 2 \times 32.8 - 57.1 \right) = 8.5 \: \text{kcal}\), whereas with propene as the model, it would be \(\left( 2 \times 30.1 - 57.1 \right) = 3.1 \: \text{kcal}\). The bond energies (Table 4-3) in combination with the heat of formation at \(25^\text{o}\) \(\left( 26.33 \: \text{kcal} \right)\) give a stabilization energy of \(5.0 \: \text{kcal}\).
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


