26.6: Correlations of Structure with Reactivity of Aromatic Compounds
- Page ID
- 22376
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This section is concerned with the quantitative correlation of reaction rates and equilibria of organic reactions with the structure of the reactants. We will restrict the discussion to benzene derivatives. The focus is on a remarkably simple treatment developed by L. P. Hammett in 1935, which has been tremendously influential. Hammett's correlation covers chemical reactivity, spectroscopy and other physical properties, and even the biological activity of drugs. Virtually all quantitative treatments of reactivity of organic compounds in solution start with the kinds of correlations that are discussed in this section.
The Hammett Equation
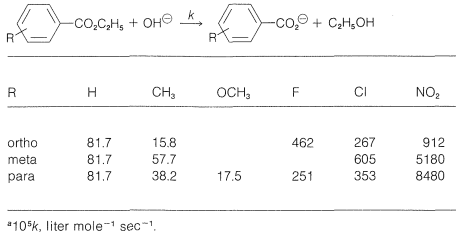
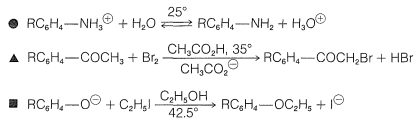
If we compare the acid strengths \(\left( K_a \right)\) of a series of substituted benzoic acids with the strength of benzoic acid itself (Table 26-4), we see that there are considerable variations with the nature of the substituent and its ring position, ortho, meta, or para. Thus all three nitrobenzoic acids are appreciably stronger than benzoic acid in the order ortho \(\gg\) para \(>\) meta. A methoxy substituent in the ortho or meta position has a smaller acid-strengthening effect, and in the para position decreases the acid strength relative to benzoic acid. Rate effects also are produced by different substituents, as is evident from the data in Table 26-5 for basic hydrolysis of some substituted ethyl benzoates. A nitro substituent increases the rate, whereas methyl and methoxy substituents decrease the rate relative to that of the unsubstituted ester.
Table 26-4: Dissociation Constants \(\left( 10^{-5} \times K_a \right)\) of Some Substituted Benzoic Acids in Water at \(25^\text{o}\)
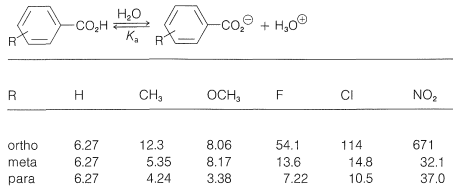
Table 26-5: Specific Rate Constants\(^a\) for Alkaline Hydrolysis of Some Substituted Ethyl Benzoates in \(85\%\) Ethanol-Water Solution at \(30^\text{o}\)
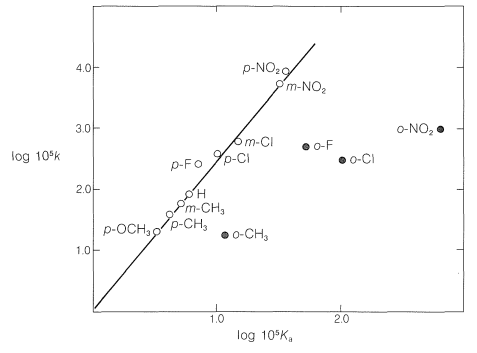
The straight line in Figure 26-3 can be expressed conveniently by Equation 26-3, in which the two variables are log \(k\) and log \(K\), the slope of the line is \(\rho\), and the intercept is \(C\):
\[\text{log} \: k = \rho \: \text{log} \: K + C \tag{26-3}\]
For the particular case for which the ring substituent is hydrogen \(\left( \ce{R=H} \right)\), Equation 26-3 becomes
\[\text{log} \: k_0 = \rho \: \text{log} \: K_0 + C \tag{26-4}\]
in which \(K_0\) is the dissociation constant of benzoic acid and \(k_0\) is the rate of hydrolysis of ethyl benzoate. Subtracting Equation 26-4 from Equation 26-3 we obtain
\[\text{log} \: \frac{k}{k_0} = \rho \: \text{log} \: \frac{K}{K_0} \tag{26-5}\]
This equation could be tested on the ratios of any rates or equilibrium constants, but it is convenient to reserve log \(\left( K/K_0 \right)\) for the dissociation of benzoic acids in water at \(25^\text{o}\) (Table 26-4) and correlate the rate or equilibrium constants for all other processes with log \(\left( K/K_0 \right)\). The common procedure is to rewrite Equation 26-5 as Equation 26-6:
\[\text{log} \: \frac{k}{k_0} = \rho \sigma \tag{26-6}\]
in which \(\sigma\) is defined as:
\[\sigma = \text{log} \: \frac{K}{K_0} \tag{26-7}\]
Equation 26-6 is known as the Hammett equation, but before we discuss its general applications, it will be helpful to say more about the \(\sigma\) term in Equation 26-7.
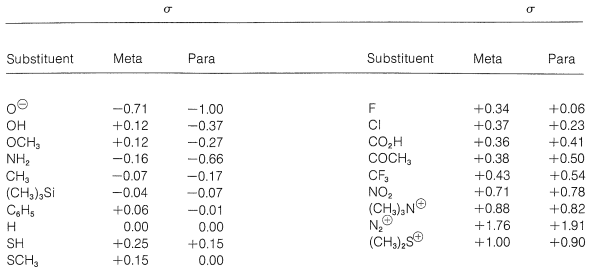
The relative strength of a substituted benzoic acid and hence the value of \(\sigma\) depends on the nature and position of the substituent in the ring. For this reason, \(\sigma\) is called the substituent constant. Table 26-6 lists several substituent constants and these will be seen to correspond to the polar character of the respective substituents. Thus the more electron-attracting a substituent is, by either resonance or induction, the more acid-strengthening it is, and the more positive is its \(\sigma\) value (relative to \(\ce{H}\) as 0.000). Conversely, the more strongly a substituent donates electrons by resonance or induction, the more negative is its \(\sigma\) value. We expect that among the more electron-attracting and electron-donating substituents will be those with electric charges, positive and negative respectively. Indeed, a diazonium group \(\left( \ce{-N_2^+} \right)\) in the para position has a very large \(\sigma\) value of +1.91, whereas a para \(\ce{-O}^\ominus\) group has a \(\sigma\) value of -1.00. In general, meta \(\sigma\) constants correspond to the inductive effect of the substituent while the para \(\sigma\) constants represent the net influence of inductive and resonance effects. If there is a substantial resonance effect, and it and the inductive effect operate in the same direction, \(\sigma_\text{para}\) will have a considerably greater magnitude than \(\sigma_\text{meta}\). The converse will be true if the resonance and inductive effects operate in opposite directions.
Table 26-6: Hammett Substituent Constants


Usually, \(\rho\) for a given reaction is influenced by conditions such as the temperature and composition of the solvent. However, the changes normally are not large unless an actual change in mechanism occurs with a change in the reaction conditions.
Scope of the Hammett Equation
The Hammett treatment provides a correlation of much experimental data. Tables 26-6 and 26-7 contain 38 substituent constants and 16 reaction constants. This means that we can calculate relative \(k\) or \(K\) values for 608 individual reactions. To illustrate, let us suppose that we need to estimate the relative rates of Reaction 16 of Table 2-7 for the para-substituents \(\ce{R} = \ce{OCH_3}\) and \(\ce{R} = \ce{CF_3}\). According to the \(\rho\) value of 4.92 for this reaction and the \(\sigma\) values of p-\(\ce{OCH_3}\) and p-\(\ce{CF_3}\) in Table 26-6, we may write
\[\text{log} \: \frac{k_{\text{p-OCH}_3}}{k_0} = 4.92 \times \left( -0.27 \right) \text{, and} \: \text{log} \: \frac{k_{\text{p-CF}_3}}{k_0} = 4.92 \times \left( 0.54 \right)\]
Subtracting these two equations gives the result:
This then is a rate ratio of 1/10,000. If we have a further table of the sixteen \(k_0\) or \(K_0\) values for the reactions listed in Table 26-7, we can calculate actual \(k\) or \(K\) values for 608 different reactions. It should be recognized that neither Table 26-6 nor Table 26-7 is a complete list; at least 80 substituent constants\(^1\) and several hundred \(\rho\) constants are now available.
The Hammett relationship formalizes and puts into quantitative terms much of the qualitative reasoning we have used for reactions involving aliphatic, alicyclic, and aromatic compounds. Considerable effort has been made to extend the Hammett idea to cover reactions other than of meta- and para-substituted benzene derivatives, but these will not be discussed here.\(^1\)
Limitations of the Hammett Equation
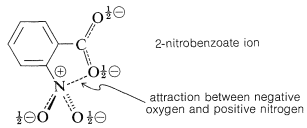
The effects of substituents in ortho positions on the reactivity of benzene derivatives do not correlate well with the Hammett equation, as can be seen in Figure 26-3. The problem is that ortho substituents are close enough to the reaction site to exert significant "proximity" effects, which may be polar as well as steric in origin. Thus the enhanced acid strength of 2-nitrobenzoic acid over the 3- and 4-isomers (see Table 26-4) may be due to a polar stabilization of the acid anion by the neighboring positive nitrogen, which of course is not possible with the 3- and 4-isomers:
In contrast, the slower rate of alkaline hydrolysis of ethyl 2-nitrobenzoate than of its 3- and 4-isomers is more likely due to a steric hindrance effect of the 2-nitro group (see Table 26-5):

Because the effect of steric hindrance on different types of reactions is not expected to be the same, a given substituent is unlikely to exert the same relative steric effect in one reaction as in another. Consequently we cannot hope to find a very simple relationship such as the Hammett equation that will correlate structure and reactivity of ortho-substituted compounds.
The Hammett equation also fails for open-chain aliphatic derivatives. For example, there is no simple linear relationship between log \(K\) for a series of substituted ethanoic acids \(\left( \ce{RCH_2CO_2H} \right)\) and log \(k\) for the hydrolysis rates of similarly substituted ethyl ethanoates \(\left( \ce{RCH_2CO_2C_2H_5} \right)\). The freedom of motion available to a flexible open-chain compound permits a much wider range of variations in steric effects than for meta- and para-substituted aromatic compounds.
The Hammett equation sometimes fails for meta- and para-substituted aromatic compounds. This failure may be expected whenever the opportunity arises for strong electron delocalization between the substituent and the reaction site. Generally, reactions that are strongly assisted by donation of electrons to the reaction site, as in \(S_\text{N}1\) reactions and electrophilic aromatic substitution, will be facilitated by electron-delocalization effects of substituents with unshared electron pairs adjacent to the aromatic group (e.g., \(\ce{-OCH_3}\), \(\ce{-OH}\), \(\ce{-O}^\ominus\), \(\ce{-NH_2}\), and \(\ce{-Cl}\)). Such reactions generally give a poor Hammett correlation. Thus a diphenylmethyl chloride with one 4-methoxy group solvolyzes in ethanol at \(25^\text{o}\) at a rate much faster than predicted by the Hammett equation, because of the resonance stabilization provided by the substituent to the intermediate carbocation:

The same type of stabilization by a 4-methoxy group does not appear to be important in influencing the ionization of 4-methoxybenzoic acid.

Similarly, those reactions that are strongly assisted by withdrawal of electrons from the reaction site, such as nucleophilic aromatic substitution, give a poor fit to a Hammett plot for the substituents that are capable of withdrawing electrons by delocalization (\(\ce{-NO_2}\), \(\ce{-N_2^+}\), \(\ce{-C \equiv N}\), and so on). An example is Reaction 16 in Table 26-7. To correlate reactivity data with structures where strong resonance effects operate, different sets of substituent constants are required.\(^1\)
\(^1\)J. Hine, Structural Effects on Equilibria in Organic Chemistry, Wiley-Interscience, New York, 1975, p. 65. This book offers a very broad coverage of quantitative correlations of substituent effects on processes as diverse as radical formation and rates of rotation around single \(\ce{C-C}\) bonds.
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


