23.7: Amines as Bases
- Page ID
- 22342
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Standard Expressions of Base Strength
Perhaps the most characteristic property of amines is their ability to act as bases by accepting protons from a variety of acids:
\[\ce{RNH_2} + \ce{HA} \rightleftharpoons \ce{R} \overset{\oplus}{\ce{N}} \ce{H_3} + \overset{\ominus}{\ce{A}}\]
When the reference acid, \(\ce{HA}\) is water, we can set up a scale of base strengths from the equilibrium constant, \(K_b\), measured for the proton-transfer reaction shown in Equation 23-3:
\[\ce{RNH_2} + \ce{H_2O} \overset{K_b}{\rightleftharpoons} \ce{R} \overset{\oplus}{\ce{N}} \ce{H_3} + \overset{\ominus}{\ce{O}} \ce{H} \tag{23-3}\]
In many reference works, it is customary to express the strengths of organic bases not as \(K_b\) but as the acid-dissociation constants, \(K_a\) (or p\(K_a\)'s) for the corresponding conjugate acids. These \(K_a\) values are then the acid constants of the corresponding ammonium ions in aqueous solution (Equation 23-4):
\[\ce{R} \overset{\oplus}{\ce{N}} \ce{H_3} + \ce{H_2O} \overset{K_a}{\rightleftharpoons} \ce{RNH_2} + \overset{\oplus}{\ce{H_2O}} \tag{23-4}\]
With this convention, the stronger the base, \(\ce{RNH_2}\), the more the equilibrium in Equation 23-4 will lie to the left, and the smaller will be \(K_a\). The relationship between \(K_a\) and \(K_b\) in water solution is
\[K_a \times K_b = 10^{-14}\]
and in terms of p\(K\) values, because by definition p\(K = -\text{log} K\),
p\(K_a\) \(+\) p\(K_b\) \(= 14\)
Base Strengths of Alkanamines and Cycloalkanamines
The base strengths of simple alkanamines usually are around \(K_b = 10^{-4}\) \(\left( K_a = 10^{-10} \right)\) in water solution, and vary within perhaps a factor of 10 from ammonia to primary, secondary, and tertiary amines, as can be seen from the data in Table 23-1. Cyclohexanamine has about the same base strength as methanamine, whereas the effect on the basic nitrogen of being in a saturated ring, as in azacyclohexane, increases the base strength somewhat.
The trends that are evident, especially from basicities of amines measured in the gas phase, point to increasing basicity with the number and size of alkyl groups on the nitrogen atom.
Order of basicity (gas phase): \(\ce{(CH_3)_3N} > \ce{(CH_3)_2NH} > \ce{CH_3NH_2} > \ce{NH_3}\)
This is reasonable because the conjugate acids, \(\ce{R_3} \overset{\oplus}{\ce{N}} \ce{H}\), are likely to be stabilized by electron-donating and polarizable alkyl groups, thereby making \(\ce{R_3N}\) a stronger base. That the same trend is not evident in aqueous solution again shows the influence of the solvent on thermochemical properties (see Section 11-8A).
Generally, substituents located on saturated groups attached to nitrogen influence base strengths through their inductive effects in the same way that these substituents influence the strengths of carboxylic acids (see Section 18-2).
Base Strengths of Arenamines
Alkenamines, or enamines, \(\ce{R-CH=CHNH_2}\), usually are not stable and rearrange readily to imines (Section 16-4C). An important exception is benzenamine (aniline), \(\ce{C_6H_5NH_2}\), which has an amino group attached to a benzene ring. The imine structure is less favorable by virtue of the considerable stabilization energy of the aromatic ring:
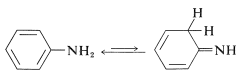
From the heat of combustion of bezenamine we know that it has a \(3 \: \text{kcal mol}^{-1}\) larger stabilization energy than benzene (Table 21-1). This difference in stabilization energies can be ascribed in either valence-bond or molecular-orbital theory to delocalization of the unshared pair of electrons on nitrogen over the benzene ring. The valence-bond structures are
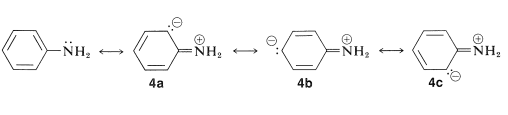
The extra \(3\)-\(\text{kcal mol}^{-1}\) stabilization energy of benzenamine can be accounted for in terms of the structures \(4a\) to \(4c\).
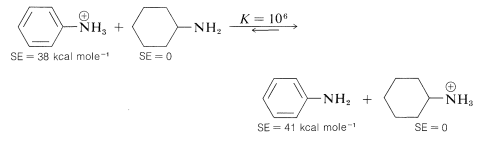
Benzenamine is only 1/1,000,000 as strong a base as cyclohexanamine. Most, if not all, of the difference can be accounted for by the decrease in stabilization when the unshared electron pair of nitrogen is localized in forming an \(\ce{N-H}\) bond. Hence, benzenamine is stabilized more in the un-ionized state by electron delocalization, relative to cyclohexanamine, than in the ionized state, as expressed by the following equilibrium which lies far to the right:
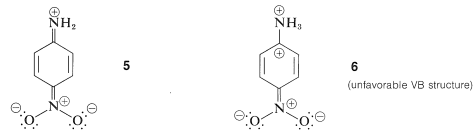
According to the valence-bond structures, \(4a\), \(4b\), and \(4c\), benzenamine has some degree of double-bond character between the nitrogen and the ring, and some degree of negative charge at the ortho and para positions. Accordingly, the ability of the amine nitrogen to add a proton should be particularly sensitive to the electrical effects produced by the presence of substituent groups on the aromatic ring. For example, carbonyl, nitro, cyano, and ethoxycarbonyl substituents, which can delocalize an electron pair on an adjacent carbon (see Sections 17-1A, 17-3E, and 18-8B), are expected to reduce the base strength of the amine nitrogen when substituted in the ortho or para positions. The reason is that stabilization by the substituent, as shown by structure \(5\) for 4-nitrobenzenamine, is important for the free base and not for the conjugate acid, \(6\):
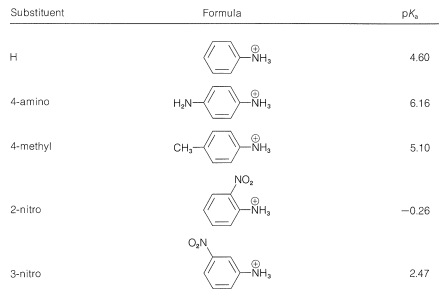
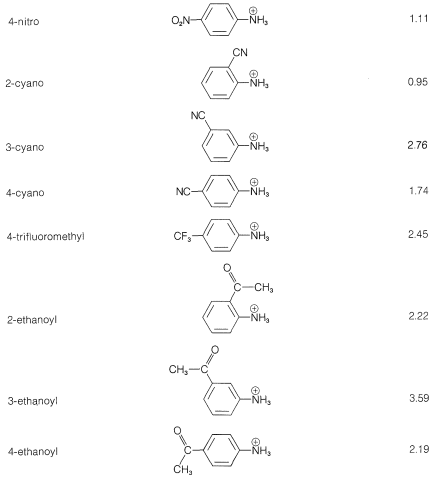
It is simpler and common practice to discuss substituent effects on base strength in terms of the dissociation equilibria of the conjugate acids, \(\ce{ArNH_3^+} + \ce{H_2O} \rightleftharpoons \ce{ArNH_2} + \ce{H_3O^+}\). Substituents that can stabilize the free base by electron delocalization or induction, as in \(5\), will tend to increase the acid dissociation of \(\ce{ArNH_3^+}\) (decrease base strength of \(\ce{ArNH_2}\)). We see this in the data of Table 23-3 for electron-withdrawing groups (\(\ce{NO_2}\), \(\ce{CN}\), \(\ce{CF_3}\), \(\ce{CH_3CO}-\)), which increase acid strengths, and for electron-donating groups (\(\ce{CH_3}\), \(\ce{NH_2}\)), which decrease acid strengths. The effect is most pronounced when the groups are at the ortho or para (2 or 4) positions.
Table 23-3: Strengths of Conjugate Acids of Monosubstituted Benzenamines in Aqueous Solution at \(25^\text{o}\)
Unsaturated Amines. Azarenes
Substantial differences in base strength are found between alkanamines and unsaturated amines that have the group \(\ce{-C=N}-\). An example is azabenzene (pyridine, \(\ce{C_5H_5N}\)), which is a nitrogen analog of benzene:
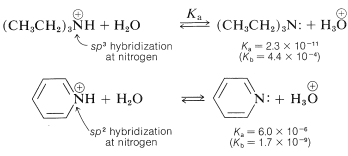
Azabenzene is quite a weak base - in fact, it is 1/100,00 as strong a base as typical alkanamines. This low basicity can be ascribed to the hybridization of the nitrogen orbitals \(\left( sp^2 \right)\) in azabenzene. As we indicated in Section 11-8B in connection with \(\ce{C-H}\) acidity, the more \(s\) character in the \(\ce{C-H}\) bonding orbital, the higher the acidity. The same arguments hold for \(\ce{N-H}\) bonds in the conjugate acids, \(\ce{-C=} \overset{\oplus}{\ce{N}} \ce{H}-\), as the following data show:
Other examples include:
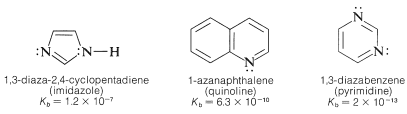
It is incorrect to assume that the basicity of unsaturated nitrogen in a \(\ce{C=N}-\) group is always low. Consider, for example, the base strength of 2,2-diaminoazaethene (guanidine):
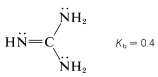
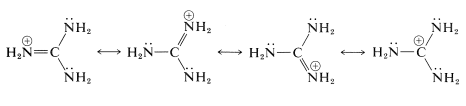
This substance is the strongest electrically neutral organonitrogen base known. The basic nitrogen is the imino \(\left( sp^2 \right)\) nitrogen, which on protonation forms a particularly stable conjugate acid in which the three \(\ce{NH_2}\) groups become identical because of electron delocalization:
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


