12.6: The Larger Cycloalkanes and their Conformations

The Baeyer strain theory suggested that the larger cycloalkanes ring are difficult to synthesize because of angle strain associated with planar rings, as calculated in Table 12-3. We now know that, except for cyclopropane, none of the cycloalkanes have planar carbon rings and that the higher cycloalkanes have normal or nearly normal bond angles. The reason that the higher cycloalkanes are generally difficult to synthesize from open-chain compounds is not so much angle strain, as Baeyer hypothesized, but the low probability of having reactive groups on the two fairly remote ends of a long hydrocarbon chain come together to effect cyclization. Usually, coupling of reactive groups on the ends of different molecules occurs in preference to cyclization, unless the reactions are carried out in very dilute solutions. This is called the high-dilution technique for achieving ring formation when the ring-forming reaction has to compete with rapid inter-molecular reactions.

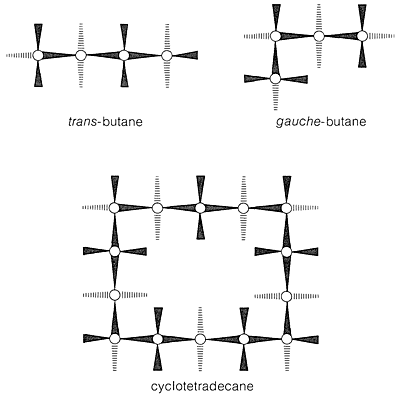
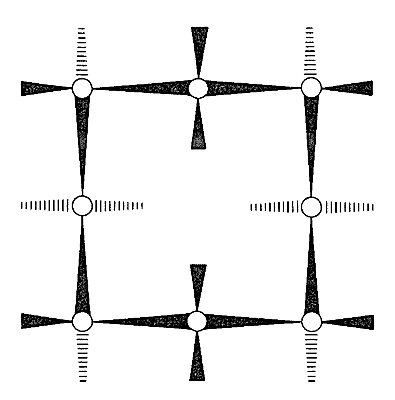
With regard to conformations of the larger cycloalkanes, we first note that the chair form of cyclohexane is a “perfect” conformation for a cycloalkane. The \(\ce{C-C-C}\) bond angles are close to their normal values, all the adjacent hydrogens are staggered with respect to one another, and the 1,3-axial hydrogens are not close enough together to experience nonbonded repulsions. About the only qualification one could put on the ideality of the chair form is that the trans conformation of butane is somewhat more stable than the gauche conformation (Section 5-2), and that all of the \(\ce{C-C-C-C}\) segments of cyclohexane have the gauche arrangement. Arguing from this, J. Dale\(^6\) has suggested that large cycloalkane rings would tend to have trans \(\ce{C-C-C-C}\) segments to the degree possible and, indeed, cyclotetradecane seems to be most stable in a rectangular conformation with trans \(\ce{C-C-C-C}\) bond segments (Figure 12-16). This conformation has a number of possible substituent positions, but because only single isomers of monosubstituted cyclotetradecanes have been isolated, rapid equilibration of the various conformational isomers must occur. Other evidence indicates that the barrier to interconversion of these conformations is about \(7 \: \text{kcal mol}^{-1}\).

Figure 12-16 Favored conformation of cyclotetradecane as proposed by Dale. For comparison, the trans and gauche forms of butane are shown by the same convention. (The convention implies that the wedged lines are \(\ce{C-C}\) or \(\ce{C-H}\) bonds projecting out of the plane of the paper, with the wide end closest to you, and the broken lines are \(\ce{C-H}\) bonds projecting behind the plane of the paper. The result is an “aerial” view of the molecule in the most stable staggered conformation.)

With the cycloalkanes having 7 to 10 carbons, there are problems in trying to make either trans or gauche \(\ce{C-C-C-C}\) segments, because the sizes of these rings do not allow the proper bond angles or torsional angles, or else there are more or less serious nonbonded repulsions. Consequently each of these rings assumes a compromise conformation with some eclipsing, some nonbonded repulsions, and some angle distortions. Brief comments on some of these conformations follow. It will be useful to use molecular models to see the interactions involved.

Cycloheptane

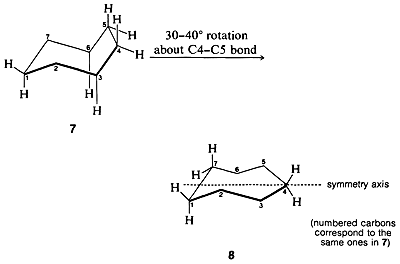
Possible conformations for cycloheptane include the “comfortable” appearing chair form, \(7\). However, this form has eclipsed hydrogens at \(\ce{C_4}\) and \(\ce{C_5}\) as well as nonbonded interactions between the axial-like hydrogens on \(\ce{C_3}\) and \(\ce{C_6}\). The best compromise conformation is achieved by a \(30^\text{o}\)-\(40^\text{o}\) rotation around the \(\ce{C_4-C_5}\) bond to relieve the eclipsing of the hydrogens. This spreads the interfering hydrogens at \(\ce{C_3}\) and \(\ce{C_6}\) and results in a somewhat less strained conformation called the twist chair. The twist chair, \(8\), is very flexible and probably only about \(3 \: \text{kcal mol}^{-1}\) of activation is required to interconvert the various possible monosubstituted cycloheptane conformations.

Cyclooctane

There are several more or less reasonable looking cyclooctane conformations. After much research it now is clear that the favored conformation is the boat-chair, \(9\), which is in equilibrium with a few tenths percent of the crown conformation, \(10\) :

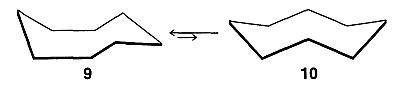
The activation energy for interconversion of these two forms is about \(10 \: \text{kcal mol}^{-1}\). The boat-chair conformation \(9\) is quite flexible and movement of its \(\ce{CH_2}\) groups between the various possible positions occurs with an activation energy of only about \(5 \: \text{kcal mol}^{-1}\).

Cyclononane

Several more or less reasonable conformations of cyclononane also can be developed, but the most favorable one is called the twist-boat-chair, which has three-fold symmetry (Figure 12-17). The activation energy for inversion of the ring is about \(6 \: \text{kcal mol}^{-1}\).

Figure 12-17: Twist boat-chair conformation of cyclononane (Public Domain; Jynto). IColor code: Carbon, C: black Hydrogen, H: white

Cyclodecane

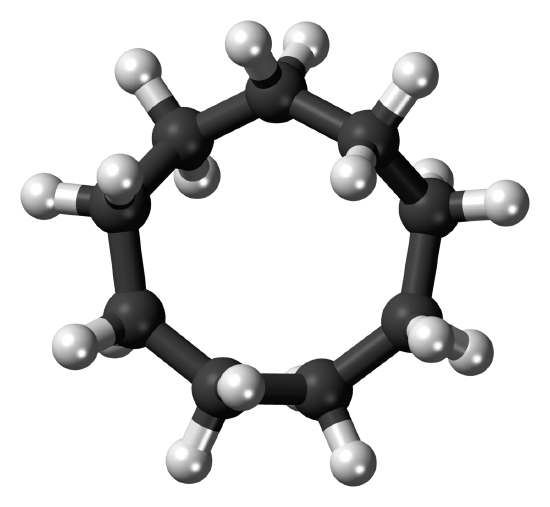
The stable conformation of cyclodecane (Figure 12-18) is similar to that of cyclotetradecane (Figure 12-16). However, there are relatively short \(\ce{H} \cdot \cdot \cdot \cdot \ce{H}\) distances and the \(\ce{C-C-C}\) bond angles are somewhat distorted because of cross-ring hydrogen-hydrogen repulsions. The most stable position for a substituent on the cyclodecane ring is the one indicated in Figure 12-18. The least stable positions are those in which a substituent replaces any of the six hydrogens shown, because nonbonded interactions are particularly strong at these positions. The activation energy for interconversion of substituent positions is about \(6 \: \text{kcal mol}^{-1}\).

Most stable conformation of cyclodecane; Dale and sawhorse representations. The shaded area in the sawhorse convention indicates substantial nonbonded \(\ce{H} \cdot \cdot \cdot \cdot \ce{H}\) interactions.

Figure 12-16).

\(^6\)Pronounced Dalluh.

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."