12.3: Conformations of Cycloalkanes

The equilibria (relative stabilities) and equilibration (rate of interconversion) of the rotational conformations of ethane and butane were discussed in Section 5-2. If you review this material, it will be clear that forming a ring from a hydrocarbon chain will greatly reduce the number of possible staggered and eclipsed conformations. We will begin our discussion with cyclohexane because of its special importance, proceed to smaller rings, then give a brief exposition of the conformations of the larger rings.

Cyclohexane Conformations

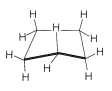
If the carbons of a cyclohexane ring were placed at the corners of a regular planar hexagon, all the \(\ce{C-C-C}\) bond angles would have to be \(120^\text{o}\). Because the expected normal \(\ce{C-C-C}\) bond angle should be near the tetrahedral value of \(109.5^\text{o}\), the suggested planar configuration of cyclohexane would have angle strain at each of the carbons, and would correspond to less stable cyclohexane molecules than those with more normal bond angles. The actual normal value for the \(\ce{C-C-C}\) bond angle of an open-chain \(\ce{-CH_2-CH_2-CH_2}-\) unit appears to be about \(112.5^\text{o}\), which is \(3^\text{o}\) greater than the tetrahedral value. From this we can conclude that the angle strain at each carbon of a planar cyclohexane would be \(\left( 120^\text{o} - 112.5^\text{o} \right) = 7.5^\text{o}\). Angle strain is not the whole story with regard to the instability of the planar form, because in addition to having \(\ce{C-C-C}\) bond angles different from their normal values, the planar structure also has its carbons and hydrogens in the unfavorable eclipsed arrangement, as shown in Figure 12-2.

Figure 12-2: Cyclohexane in the strained planar configuration showing how the hydrogens become eclipsed.

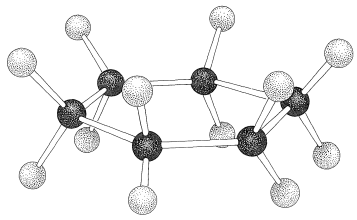
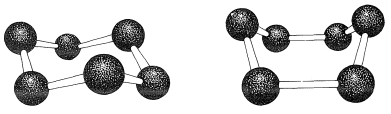
If the carbon valence angles are kept near the tetrahedral value, you will find that you can construct ball-and-stick models of the cyclohexane six-carbon ring with two quite different conformations. These are known as the "chair" and "boat" conformations (Figure 12-3). It has not been possible to separate cyclohexane at room temperature into pure isomeric forms that correspond to these conformations, and actually the two forms appear to be rapidly interconverted. The chair conformation is considerably more stable and comprises more than \(99.9\%\) of the equilibrium mixture at room temperature.\(^1\)

Figure 12-3: Chair (left) and boat (right) conformations of the six carbons of a cyclohexane ring with normal \(\ce{C-C-C}\) bond angles.

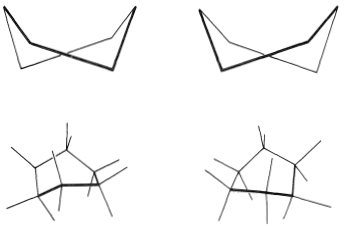
Why is the boar form less stable than the chair form, if both have normal \(\ce{C-C-C}\) bond angles? The answer is that the boat form has unfavorable nonbonded interactions between the hydrogen atoms around the ring. If we make all of the bond angles normal and orient the carbons to give the "extreme boat" conformation of Figure 12-4, a pair of 1,4 hydrogens (the so-called "flagpole" hydrogens) have to be very close together \(\left( 1.83 \: \text{Å} \right)\). Hydrogens this close together would be on the rising part of a repulsion potential energy curve, such as Figure 4-6, for hydrogen-hydrogen nonbonded interactions. This steric hindrance at an \(\ce{H-H}\) distance of \(1.83 \: \text{Å}\) corresponds to a repulsion energy of about \(3 \: \text{kcal mol}^{-1}\). There is still another factor that makes the extreme boat unfavorable; namely, that the eight hydrogens along the "sides" of the boat are eclipsed, which brings them substantially closer together than they would be in a staggered arrangement (about \(2.27 \: \text{Å}\) compared with \(2.50 \: \text{Å}\)). This is in striking contrast with the chair form (Figure 12-5), for which adjacent hydrogens are in staggered positions with respect to one another all around the ring. Therefore the chair form is expected to be more stable than the boat form because it has less repulsion between the hydrogens.

Figure 12-4: Extreme boat form of cyclohexane showing interfering and eclipsed hydrogens. Top, space-filling model; center, ball-and-stick model; bottom, sawhorse representations.

Figure 12-5: Chair form of cyclohexane showing equatorial and axial hydrogens. Top, space-filling model; center, ball-and-stick model; bottom, sawhorse representation. Notice that all the axial positions are equivalent and all the equatorial positions are equivalent. By this we mean that a substituent on any one of the six axial positions gives the same axial conformation, whereas a substituent on any one of the six equatorial positions gives the same equatorial conformation.

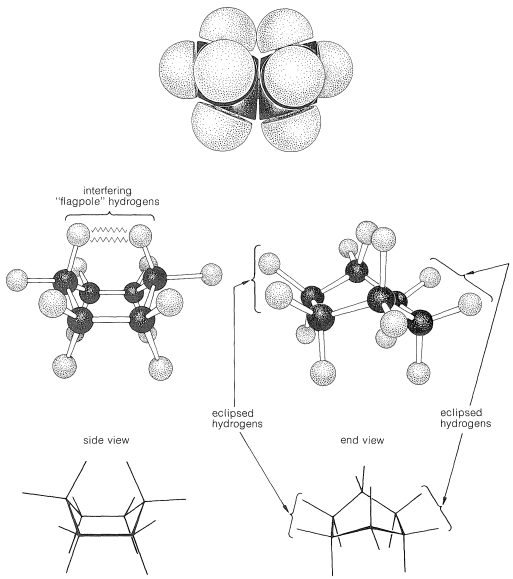
You should make and inspect models such as those in Figure 12-3 to see the rather striking difference between the chair and boat conformations that is not obvious from the diagrams. You will find that the chair structure is quite rigid, and rotation does not occur around the \(\ce{C-C}\) bonds with interconversion to the boat structure. In contrast, the boat form is quite flexible. Rotation about the \(\ce{C-C}\) bonds permits the ring to twist one way or the other from the extreme boat conformation to considerably more stable, equal-energy conformations, in which the flagpole hydrogens move farther apart and the eight hydrogens along the sides become largely but not completely staggered. These arrangements are called the twist-boat (sometimes skew-boat) conformations (see Figure 12-6) and are believed to be about \(5 \: \text{kcal mol}^{-1}\) less stable than the chair form.

Figure 12-6: The twist-boat conformations of cyclohexane.

It is possible to measure the spectral properties of the twist-boat form by a very elegant technique employed by F. A. L. Anet. Because the equilibrium constant for conversion of chair to boat increases with temperature, a considerable proportion of the molecules exist as the twist-boat form in the vapor at \(800^\text{o}\). If such vapor is allowed to impinge on a surface cooled to \(20 \: \text{K}\), the film condensate contains about \(25\%\) of the twist-boat form. At this low temperature, the twist-boat form is converted to the more stable chair form at a very slow rate. Infrared spectra can be taken of the boat-chair mixture at \(10 \: \text{K}\). If the mixture is allowed to warm to \(75 \: \text{K}\), the normal equilibrium favoring the chair form is established in a short time.

Dreiding Models

The spatial arrangement (stereochemistry) of cyclohexane and other organic compounds are studied conveniently with the aid of Dreiding models, which are made with standard bond angles and scaled bond distances. The bonds have stainless-steel rods that make a snap-fit into stainless-steel sleeves. Rotation is smooth about the bonds and there is sufficient flexibility to accommodate some angle strain. Dreding models of the conformations of cyclohexane are shown in Figure 12-7. Notice that these models correspond closely to the sawhorse representations in Figures 12-4, 12-5, and 12-6.

Figure 12-7: Dreiding models of the cyclohexane conformations.

Conformational Equilibria and Equilibration for Cyclohexane Derivatives

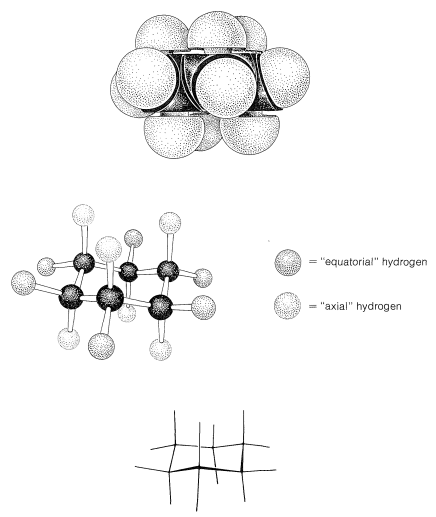
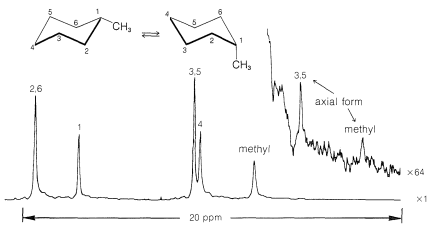
Figure 12-5 shows that there are two distinct kinds of hydrogen in the chair form of cyclohexane - six that are close to the "average" plane of the ring (called equatorial hydrogens) and three above and three below this average plane (called axial hydrogens). This raises interesting questions in connection with substituted cyclohexanes: For example, is the methyl group in methylcyclohexane equatorial or axial? Since only one methylcyclohexane is known, the methyl group must be exclusively equatorial \(\left( e \right)\), exclusively axial \(\left( a \right)\), or the two forms must be interconverted so rapidly that they cannot be separated into isomeric forms. It appears that the latter circumstance prevails, with the ring changing rapidly from one chair form to another by flipping one end of the chair up and the other end down:

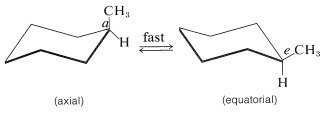
Such a change would cause a substituent in an axial position to go to an equatorial position and vice versa. This process is called ring inversion and its rate often is called the inversion frequency. With cyclohexane, inversion is so fast at room temperature that, on average, the molecules, flip about 100,000 times per second, over an energy barrier of about \(11 \: \text{kcal mol}^{-1}\).

You will understand this flipping process if you make a model of a cyclohexane ring carrying a single substituent. By manipulating the model you can discover some of the different ways the process can occur. The simplest route is simply to flip up one corner of the ring to convert the chair into a boat and then flip down the opposite carbon:

Because of the flexibility of the boat conformation, it is possible to transform it to other boat conformations whereby carbons other than the one indicated flip down and complete the interconversion.

At room temperature the conformation of methylcyclohexane with the methyl equatorial is more stable than the one with the methyl axial by \(1.7 \: \text{kcal mol}^{-1}\). The same is true of all monosubstituted cyclohexanes to a greater or lesser degree. Reasons for this can be seen from space-filling models (Figure 12-8), which show that a substituent group has more room when the substituent is equatorial than when it is axial. In the axial position the substituent is considerably closer to the two axial hydrogens on the same side of the ring than to other hydrognes, even hydrogens on adjacent carbons when the substituent is in the equatorial position (Figure 12-8). For example, when the substituent is bromine, which has a \(\ce{C-Br}\) bond length of \(1.94 \: \text{Å}\), the distance from axial bromine to the axial hydrogen at \(\ce{C_3}\) or \(\ce{C_5}\) on the same side of the ring is about \(2.7 \: \text{Å}\). In contrast, the distance from equatorial bromine to any of the hydrogens on the adjacent carbons is about \(3.1 \: \text{Å}\).

Figure 12-8: Space-filling models of equatorial and axial chair conformations of cyclohexyl bromide. Significant nonbonded interactions are indicated for the sawhorse formulas by dashed lines; these interactions are more severe in the axial than the equatorial conformation.

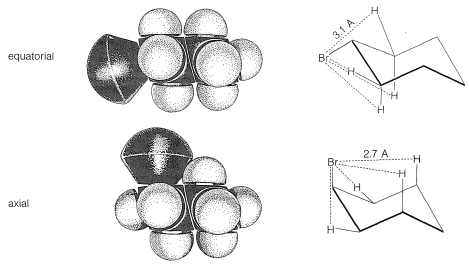
There is a very important general aspect of the difference between these two nonbonded \(\ce{H} \cdot \cdot \cdot \ce{Br}\) interactions at \(2.7 \: \text{Å}\) and \(3.1 \: \text{Å}\). Whenever two nonbonded atoms are brought close together, and before the massive repulsion sets in (which is so evident in Figure 4-6), there is a slight dip in the energy curve corresponding to attraction.\(^2\) For nonbonded \(\ce{H} \cdot \cdot \cdot \ce{Br}\) interactions the bottom of the dip comes at about \(3.1 \: \text{Å}\) (Figure 12-9), and the resulting attraction between the atoms will provide some stabilization of the equatorial conformation relative to the axial conformation.

Figure 4-6). Other nonbonded pairs of atoms have similar curves, but with different positions and depths of the minima. The minima usually are considerably deeper with atoms of higher atomic number. The ratios of the attractive forces at the lowest point for \(\ce{He} \cdot \cdot \cdot \ce{He}\), \(\ce{Ne} \cdot \cdot \cdot \ce{Ne}\), \(\ce{Ar} \cdot \cdot \cdot \ce{Ar}\), \(\ce{Kr} \cdot \cdot \cdot \ce{Kr}\), and \(\ce{Xe} \cdot \cdot \cdot \ce{Xe}\) are 1:4:14:21:28.

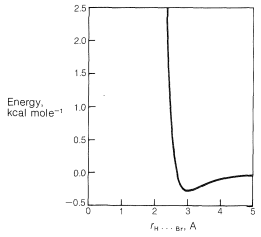
Weak attractive forces between nonbonded atoms are called van der Waals attractive forces, London\(^3\) forces, or dispersion forces, and are of great importance in determining the properties of liquids. They also can be expected to play a role in determining conformation equilibria whenever the distances between the atoms in the conformations correspond to the so-called van der Walls minima.

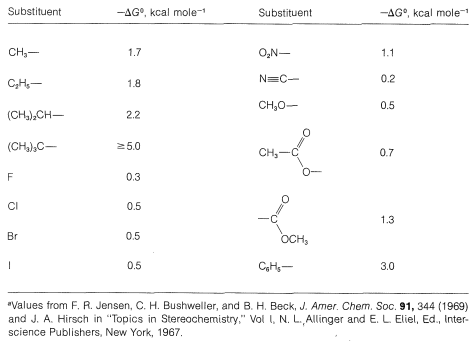
Table 12-2 shows the contribution made by various substituents to the free-energy change from the axial to the equatorial orientations of the substituent. Thus, for bromine, the free-energy change, \(\Delta G^0\), is \(-0.5 \: \text{kcal mol}^{-1}\), which means that at \(25^\text{o}\), the equilibrium constant, \(K\), for the axial \(\rightleftharpoons\) equatorial equilibrium is about 2.3 (from \(-2.303 RT \: \text{log} \: K = \Delta G^0\); see Section 4-4A).

From many studies it is known that the interconversion of conformations with the substituent in the equatorial and the axial positions occurs about 100,000 times per second, which corresponds to a transition-state energy (activation energy) of about \(11 \: \text{kcal mol}^{-1}\) above the ground-state energy. The rate decreases as the temperature is lowered. If one cools chlorocyclohexane to its melting point \(\left( -44^\text{o} \right)\), the substance crystallizes to give the pure equatorial isomer. The crystals then can be cooled to \(-150^\text{o}\) and dissolved at this temperature in a suitable solvent. At \(-150^\text{o}\) it would take about 130 days for half of the equatorial form to be converted to the axial form. However, when the solution is warmed to \(-60^\text{o}\) the equatorial conformation is converted to the equilibrium mixture in a few tenths of a second.

Table 12-2: A Selection of \(\Delta G^0\) for the Change from Axial to Equatorial Orientation of Substituents for Monosubstituted Cyclohexanes

Cis-Trans Isomerism and Conformational Equilibria for Cyclohexane Derivatives

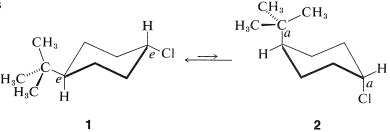
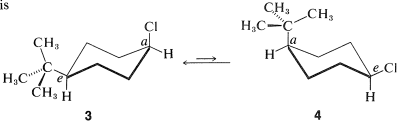
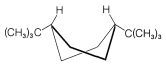
The cis-trans isomerism of cyclohexane derivatives (Section 5-1A) is complicated by conformational isomerism. For example, 4-tert-butylcyclohexyl chloride theoretically could exist in four stereoisomeric chair forms, \(1\), \(2\), \(3\), and \(4\).

trans

cis

Figure 12-11).

Figure 12-10: 1,3-interactions in a cyclohexane ring with an axial tert-butyl group.

Figure 12-11: Twist-boat conformation of cis-1,4-di-tert-butylcyclohexane.

Use of \(\ce{^{13}C}\) nmr spectroscopy to determine whether a substituent is in an axial or equatorial position is well illustrated with cis- and trans-4-tert-butylcyclohexanols, \(5\) and \(6\):

Figure 12-12. At \(-110^\text{o}\), the equatorial form is \(99\%\) of the mixture and is interconverted only very slowly with the \(1\%\) of axial form. Despite the strong \(\ce{^{13}C}\) nmr signals from the equatorial form, the chemical shifts of \(\ce{C_3}\), \(\ce{C_5}\), and \(\ce{CH_3}\) carbons of the axial form are sufficiently different that they can be seen upfield of the methyl resonance of the equatorial form.

Figure 12-12: Proton-decoupled, \(63.1 \: \text{MHz}\), \(\ce{^{13}C}\) spectrum of methylcyclohexane at \(-110^\text{o}\). The upper right curve was taken with the signal sensitivity control turned up by a factor of 64. (Courtesy of Dr. F. A. L. Anet.)

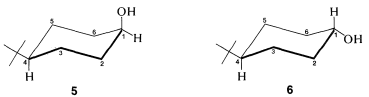
Cyclopentane

The five \(\ce{-CH_2}-\) groups of cyclopentane theoretically could form a regular planar pentagon (internal angles of \(108^\text{o}\)) with only a little bending of the normal \(\ce{C-C-C}\) bond angles. Actually, cyclopentane molecules are not flat. The planar structure has completely eclipsed hydrogens, which makes it less stable by about \(10 \: \text{kcal mol}^{-1}\) than if there were no eclipsed hydrogens. The result is that each molecule assumes a puckered conformation that is the best compromise between distortion of bond angles and eclipsing of hydrogens. The best compromise conformations have the ring twisted with one or two of the \(\ce{-CH_2}-\) groups bent substantially out of a plane passed through the other carbons (Figure 12-14). The flexibility of the ring is such that these deformations move rapidly around the ring.

Figure 12-14: Nonplanar conformation of cyclopentane. Notice that the forward carbon is out of the plane of the other four.

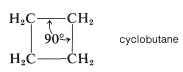
Cyclobutane

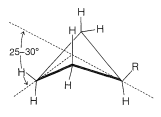
Formation of a four-membered ring of carbon atoms can be achieved only with substantial distortion of the normal valence angles of carbon, regardless of whether the ring is planar or nonplanar. In cyclobutane, for example, if the valence bonds are assumed to lie along straight lines drawn between the carbon nuclei, each \(\ce{C-C-C}\) bond angle will be \(19.5^\text{o}\) smaller than the \(109.5^\text{o}\) tetrahedral value:

Figure 12-15).

Figure 12-15: Nonplanar cyclobutane conformation with a substituent \(\ce{R}\) in the less hindered, quasi-equatorial position. The dihedral angle between the two halves of the bent ring usually is \(25^\text{o}\) to \(30^\text{o}\), that is, a \(25^\text{o}\) to \(30^\text{o}\) deviation from planarity.

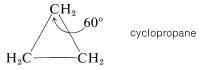
Cyclopropane

The three carbon atoms of the cyclopropane ring lie in a plane. Therefore the angle strain is expected to be considerable because each \(\ce{C-C-C}\) valence angle must be deformed \(49.5^\text{o}\) from the tetrahedral value. It is likely that some relief from the strain associated with the eclipsing of the hydrogens of cyclopropane is achieved by distortion of the \(\ce{H-C-H}\) and \(\ce{H-C-C}\) bond angles:

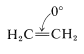
"Cycloethane" (Ethene)

If one is willing to consider a carbon-carbon double bond as a two-membered ring, then ethene, \(\ce{C_2H_4}\), is the simplest possible cycloalkane ("cycloethane"). As such, \(\ce{C_2H_4}\) has \(\ce{C-C-C}\) valence angles of \(0^\text{o}\) and therefore an angle strain of \(109.5^\text{o}\) at each \(\ce{CH_2}\) group compared to the tetrahedral value:

Contributors and Attributions

John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."

---

\(^1\)Pioneering work on the conformations of cyclohexane and its derivatives was carried out by O. Hassel (Norway) and D. H. R. Barton (United Kingdom) for which they shared a Nobel Prize in 1969.

\(^2\)The vertical scale of Figure 4-6 does not permit seeing the dip in the curve resulting from attractive forces between neon atoms. It is deepest when \(r\) is about \(3.12 \: Å\) and amounts to \(0.070 \: \text{kcal mol}^{-1}\).

\(^3\)After F. London, who developed a quantum-mechanical theory of the origin of these forces and also pioneered many quantum calculations of great consequence to chemistry, including bonding in \(\ce{H_2}\), which will be discussed in Section 21-1.