8.5: Mechanisms of Nucleophilic Substitution Reactions
- Page ID
- 22214
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two simple mechanisms can be written for the reaction of chloromethane with hydroxide ion in aqueous solution that differ in the timing of bond breaking relative to bond making. In the first mechanism, \(A\), the overall reaction is the result of two steps, the first of which involves a slow dissociation of chloromethane to solvated methyl carbocation\(^4\) and solvated chloride ion. The second step involves a fast reaction between the carbocation and hydroxide ion (or water) to yield methanol.
Mechanism \(A\):
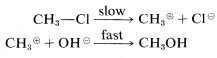
or
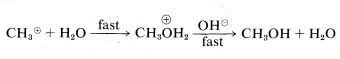
In the second mechanism, \(B\), the reaction proceeds in a single step. Attack of hydroxide ion at carbon occurs simultaneously with the loss of chloride ion; that is, the carbon-oxygen bond is formed as the carbon-chlorine bond is broken:
Mechanism \(B\):
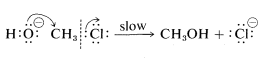
Both of these mechanisms are important in the displacement reactions of alkyl compounds, although chloromethane appears to react only by Mechanism \(B\). Now we will discuss the criteria for distinguishing between the concerted and stepwise mechanisms.
Kinetics of Substitution Mechanisms
Of the two mechanisms, \(A\) requires that the reaction rate be determined solely by the rate of the first step (cf. earlier discussion in Section 4-4C). This means that the rate at which methanol is formed (measured in moles per unit volume per unit time) will depend on the chloromethane concentration, but not on the hydroxide ion concentration, because hydroxide ion is not utilized except in a fast secondary reaction. In contrast, Mechanism \(B\) requires the rate to depend on the concentrations of both reagents because the slow step involves collisions between hydroxide ions and chloromethane molecules.
\[ v = k_A [CH_3Cl] \label{8-1}\]
\[ v = k_B [CH_3Cl][OH^-] \label{8-2}\]
More precisely, the reaction rate (\(\nu\)) may be expressed in terms of Equation \(\ref{8-1}\) for Mechanism \(A\) and Equation \(\ref{8-2}\) for Mechanism \(B\):
Customarily, \(\nu\) is expressed in moles of product formed per liter of solution per unit of time (most frequently in seconds). The concentration terms \(\left[ CH_3Cl \right]\) and \(\left[ OH^\ominus \right]\) are then in units of moles per liter, and the proportionality constant \(k\) (called the specific rate constant) has the units of \(\text{sec}^{-1}\) for Mechanism \(A\) and \(\text{mol}^{-1} \times \text{L} \times \text{sec}^{-1}\) for Mechanism \(B\).
It is important to recognize the difference between the order of a reaction with respect to a specific reactant and the overall order of a reaction. The order of a reaction with respect to a particular reactant is the power to which the concentration of that reactant must be raised to have direct proportionality between concentration and reaction rate. According to Equation \(\ref{8-2}\) the rate of the chloromethane-hydroxide ion reaction is first order with respect to chloromethane and first order with respect to hydroxide ion. In Equation \(\ref{8-1}\) the rate is first order with respect to chloromethane and zero order with respect to hydroxide ion because \(\left[ OH^\ominus \right]^0 = 1\). The overall order of reaction is the sum of the orders of the respective reactants. Thus Equations \(\ref{8-1}\) and \(\ref{8-2}\) express the rates of overall first-order and second-order reactions, respectively.
We can use the overall reaction order to distinguish between the two possible mechanisms, \(A\) and \(B\). Experimentally, the rate of formation of methanol is found to be proportional to the concentrations both of chloromethane and of hydroxide ion. Therefore the reaction rate is second order overall and is expressed correctly by Equation \(\ref{8-2}\). This means that the mechanism of the reaction is the single-step process \(B\). Such reactions generally are classified as bimolecular nucleophilic substitutions, often designated \(\text{S}_\text{N}2\), \(\text{S}\) for substitution, \(\text{N}\) for nucleophilic, and \(2\) for bimolecular, because there are two reactant molecules in the transition state. To summarize: For an \(\text{S}_\text{N}2\) reaction,
- rate:
\[ v = k[RX][Y] \label{8-3}\]
- mechanism:
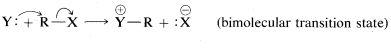
The stepwise Mechanism \(A\) is a unimolecular nucleophilic substitution and accordingly is designated \(\text{S}_\text{N}1\). The numeral \(1\) (or \(2\)) used in these designations does not refer to the kinetic order of the reaction, but refers to the number of molecules (not including solvent molecules) that make up the transition state. Thus for \(\text{S}_\text{N}1\),
- rate:
\[ v = k[RX] \label{8-4}\]
- mechanism:

or
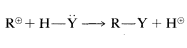
Solvolysis
Many \(\text{S}_\text{N}\) reactions are carried out using the solvent as the nucleophilic agent. They are called solvolysis reactions and involve solvents such as water, ethanol, ethanoic acid, and methanoic acid. Two examples are

In these examples, solvolysis is necessarily a first-order reaction, because normally the solvent is in such great excess that its concentration does not change appreciably during reaction, and hence its contribution to the rate does not change. However, that the overall rate is first order does not mean the reaction necessarily proceeds by an \(\text{S}_\text{N}1\) mechanism, particularly in solvents such as water, alcohols, or amines, which are reasonably good nucleophilic agents. The solvent can act as the displacing agent in an \(\text{S}_\text{N}2\) reaction.
To distinguish between \(\text{S}_\text{N}1\) and \(\text{S}_\text{N}2\) mechanisms of solvolysis requires other criteria, notably stereochemistry (Sections 8-5 and 8-6), and the effect of added nucleophiles on the rate and nature of the reaction products. For example, it often is possible to distinguish between \(\text{S}_\text{N}1\) and \(\text{S}_\text{N}2\) solvolysis by adding to the reaction mixture a relatively small concentration of a substance that is expected to be a more powerful nucleophile than the solvent. If the reaction is strictly \(\text{S}_\text{N}1\), the rate at which \(RX\) disappears should remain essentially unchanged because it reacts only as fast as \(R^\oplus\) forms, and the rate of this step is not changed by addition of the nucleophile, even if the nucleophile reacts with \(R^\oplus\). However, if the reaction is \(\text{S}_\text{N}2\), the rate of disappearance of \(RX\) should increase because \(RX\) reacts with the nucleophile in an \(\text{S}_\text{N}2\) reaction and now the rate depends on both the nature and the concentration of the nucleophile.
\(^4\)Many organic chemists, and indeed the previous versions of this book, use the term "carbonium ion" for species of this kind. However, there is well-established usage of the -onium suffix, for ammonium, oxonium, chloronium, and so on, to denote positively charged atoms with filled valence shells. In the interest of greater uniformity of nomenclature we shall use "carbocation" for carbon positive ions that have unfilled valence shells (6 electrons).
Contributors and Attributions
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."


