9.5: Chemical Equilibrium

Last updated
Save as PDF

Page ID: 227634

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Outcomes

Explain chemical equilibrium.
Write expression for calculating \(K\).
Calculate and compare Q and K values.
Predict relative amounts of reactants and products based on equilibrium constant \(K\).

Hydrogen and iodine gases react to form hydrogen iodide according to the following reaction:

\[\ce{H_2} \left( g \right) + \ce{I_2} \left( g \right) \rightleftharpoons 2 \ce{HI} \left( g \right) \nonumber \]

\[\begin{align} &\text{Forward reaction:} \: \: \ce{H_2} \left( g \right) + \ce{I_2} \left( g \right) \rightarrow 2 \ce{HI} \left( g \right) \\ &\text{Reverse reaction:} \: \: 2 \ce{HI} \left( g \right) \rightarrow \ce{H_2} \left( g \right) + \ce{I_2} \left( g \right) \end{align} \nonumber \]

Initially, only the forward reaction occurs because no \(\ce{HI}\) is present. As soon as some \(\ce{HI}\) has formed, it begins to decompose back into \(\ce{H_2}\) and \(\ce{I_2}\). Gradually, the rate of the forward reaction decreases while the rate of the reverse reaction increases. Eventually the rate of combination of \(\ce{H_2}\) and \(\ce{I_2}\) to produce \(\ce{HI}\) becomes equal to the rate of decomposition of \(\ce{HI}\) into \(\ce{H_2}\) and \(\ce{I_2}\). When the rates of the forward and reverse reactions have become equal to one another, the reaction has achieved a state of balance. Chemical equilibrium is the state of a system in which the rate of the forward reaction is equal to the rate of the reverse reaction.

Chemical equilibrium can be attained whether the reaction begins with all reactants and no products, all products and no reactants, or some of both. The figure below shows changes in concentration of \(\ce{H_2}\), \(\ce{I_2}\), and \(\ce{HI}\) for two different reactions. In the reaction depicted by the graph on the left (A), the reaction begins with only \(\ce{H_2}\) and \(\ce{I_2}\) present. There is no \(\ce{HI}\) initially. As the reaction proceeds towards equilibrium, the concentrations of the \(\ce{H_2}\) and \(\ce{I_2}\) gradually decrease, while the concentration of the \(\ce{HI}\) gradually increases. When the curve levels out and the concentrations all become constant, equilibrium has been reached. At equilibrium, concentrations of all substances are constant.

In reaction B, the process begins with only \(\ce{HI}\) and no \(\ce{H_2}\) or \(\ce{I_2}\). In this case, the concentration of \(\ce{HI}\) gradually decreases while the concentrations of \(\ce{H_2}\) and \(\ce{I_2}\) gradually increase until equilibrium is again reached. Notice that in both cases, the relative position of equilibrium is the same, as shown by the relative concentrations of reactants and products. The concentration of \(\ce{HI}\) at equilibrium is significantly higher than the concentrations of \(\ce{H_2}\) and \(\ce{I_2}\). This is true whether the reaction began with all reactants or all products. The position of equilibrium is a property of the particular reversible reaction and does not depend upon how equilibrium was achieved.

Conditions for Equilibrium and Types of Equilibrium

It may be tempting to think that once equilibrium has been reached, the reaction stops. Chemical equilibrium is a dynamic process. The forward and reverse reactions continue to occur even after equilibrium has been reached. However, because the rates of the reactions are the same, there is no change in the relative concentrations of reactants and products for a reaction that is at equilibrium. The conditions and properties of a system at equilibrium are summarized below.

The system must be closed, meaning no substances can enter or leave the system.
Equilibrium is a dynamic process. Even though we don't necessarily see the reactions, both forward and reverse are taking place.
The rates of the forward and reverse reactions must be equal.
The amount of reactants and products do not have to be equal. However, after equilibrium is attained, the amounts of reactants and products will be constant.

The description of equilibrium in this concept refers primarily to equilibrium between reactants and products in a chemical reaction. Other types of equilibrium include phase equilibrium and solution equilibrium. A phase equilibrium occurs when a substance is in equilibrium between two states. For example, a stoppered flask of water attains equilibrium when the rate of evaporation is equal to the rate of condensation. A solution equilibrium occurs when a solid substance is in a saturated solution. At this point, the rate of dissolution is equal to the rate of recrystallization. Although these are all different types of transformations, most of the rules regarding equilibrium apply to any situation in which a process occurs reversibly.

Two people are shown throwing juggling pins back and forth to one another.

Red blood cells transport oxygen to the tissues so they can function. In the absence of oxygen, cells cannot carry out their biochemical responsibilities. Oxygen moves to the cells attached to hemoglobin, a protein found in the red cells. In cases of carbon monoxide poisoning, \(\ce{CO}\) binds much more strongly to the hemoglobin, blocking oxygen attachment and lowering the amount of oxygen reaching the cells. Treatment involves the patient breathing pure oxygen to displace the carbon monoxide. The equilibrium reaction shown below illustrates the shift toward the right when excess oxygen is added to the system:

\[\ce{Hb(CO)_4} \left( aq \right) + 4 \ce{O_2} \left( g \right) \rightleftharpoons \ce{Hb(O_2)_4} \left( aq \right) + 4 \ce{CO} \left( g \right) \nonumber \]

Equilibrium Constant

Consider the hypothetical reversible reaction in which reactants \(\ce{A}\) and \(\ce{B}\) react to form products \(\ce{C}\) and \(\ce{D}\). This equilibrium can be shown below, where the lowercase letters represent the coefficients of each substance.

\[a \ce{A} + b \ce{B} \rightleftharpoons c \ce{C} + d \ce{D} \nonumber \]

As we have established, the rates of the forward and reverse reactions are the same at equilibrium, and so the concentrations of all of the substances are constant. Since that is the case, it stands to reason that a ratio of the concentration for any given reaction at equilibrium maintains a constant value. The equilibrium constant \(\left( K_\text{eq} \right)\) is the ratio of the mathematical product of the products of a reaction to the mathematical product of the concentrations of the reactants of the reaction. Each concentration is raised to the power of its coefficient in the balanced chemical equation. For the general reaction above, the equilibrium constant expression is written as follows:

\[K_\text{eq} = \frac{\left[ \ce{C} \right]^c \left[ \ce{D} \right]^d}{\left[ \ce{A} \right]^a \left[ \ce{B} \right]^b} \nonumber \]

The concentrations of each substance, indicated by the square brackets around the formula, are measured in molarity units \(\left( \text{mol/L} \right)\).

The value of the equilibrium constant for any reaction is only determined by experiment. As detailed in the above section, the position of equilibrium for a given reaction does not depend on the starting concentrations and so the value of the equilibrium constant is truly constant. It does, however, depend on the temperature of the reaction. This is because equilibrium is defined as a condition resulting from the rates of forward and reverse reactions being equal. If the temperature changes, the corresponding change in those reaction rates will alter the equilibrium constant. For any reaction in which a \(K_\text{eq}\) is given, the temperature should be specified.

The equilibrium constant can vary over a wide range of values. Because products are in the numerator of the equilibrium constant expression and reactants are in the denominator, values of K greater than \(10^3\) indicate a strong tendency for reactants to form products. In this case, chemists say that equilibrium lies to the right as written, favoring the formation of products. An example is the reaction between \(H_2\) and \(Cl_2\) to produce \(HCl\), which has an equilibrium constant of \(1.6 \times 10^{33}\) at 300 K. Because \(H_2\) is a good reducing agent and \(Cl_2\) is a good oxidizing agent, the reaction proceeds essentially to completion.

\(H_{2(g)}+Cl_{2(g)} \rightleftharpoons 2HCl_{(g)}\) \(K\)=\(1.6 \times 10^{33}\) at 300K

In contrast, values of \(K\) less than \(10^{-3}\) indicate that the ratio of products to reactants at equilibrium is very small. That is, reactants do not tend to form products readily, and the equilibrium lies to the left as written, favoring the formation of reactants. An example is the decomposition of water. No wonder you won’t find water a very good source of oxygen gas and hydrogen gas at ordinary temperatures!

\(H_2O_{(g)} \rightleftharpoons H_{2(g)} + ½ O_{2(g)}\) \(K\)=\(8 \times 10^{-41}\) at 25°C

Figure \(\PageIndex{4}\) summarizes the relationship between the magnitude of K and the relative concentrations of reactants and products at equilibrium for a general reaction, written as reactants \(\rightleftharpoons\) products.

Figure \(\PageIndex{4}\): The Relationship between the Composition of the Mixture at Equilibrium and the Magnitude of the Equilibrium Constant. The larger the K, the farther the reaction proceeds to the right before equilibrium is reached, and the greater the ratio of products to reactants at equilibrium.

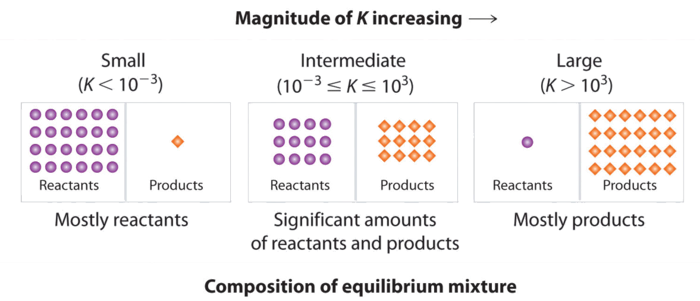
A large value of the equilibrium constant \(K\) means that products predominate at equilibrium; a small value means that reactants predominate at equilibrium.

When \(K\) is a very large number, the reaction is essentially irreversible, products predominate at equilibrium.
When \(K\) is between 1 and 1000, more products than reactants are present at equilibrium
When \(K\) is between 1 and 0.001, more reactants than products are present at equilibrium.
When \(K\) is a very small number, the reaction produces almost no products; only reactants are present at equilibrium.

Example \(\PageIndex{1}\)

Write the expression for the equilibrium constant K for the following reaction:

N₂ (g) + 3 H₂ (g) ⇄ 2 NH₃ (g)

Solution

The equilibrium constant equation is the ratio of the concentration of the products (NH₃) to the concentration of the reactants (N₂ and H₂), each raised to the power of its coefficient in the balanced chemical equation.

\(K=\dfrac{[NH_3]^2}{[N_2][H_2]^3}\)

Exercise \(\PageIndex{1}\)

Write the expression of the equilibrium constant K for the following reaction:.

2 NOCl (g) ⇄ 2 NO (g) + Cl₂ (g)

Answer: \(K=\dfrac{[NO]^2[Cl_2]}{[NOCl]^2}\)

Example \(\PageIndex{2}\)

Predict which systems at equilibrium will (a) contain essentially only products, (b) contain essentially only reactants, and (c) contain appreciable amounts of both products and reactants.

\(H_{2(g)}+I_{2(g)} \rightleftharpoons 2HI_{(g)}\;\;\; K_{(700K)}=54\)
\(2CO_{2(g)} \rightleftharpoons 2CO_{(g)}+O_{2(g)}\;\;\; K_{(1200K)}=3.1 \times 10^{−18}\)
\(PCl_{5(g)} \rightleftharpoons PCl_{3(g)}+Cl_{2(g)}\;\;\; K_{(613K)}=97\)
\(2O_{3(g)} \rightleftharpoons 3O_{2(g)} \;\;\; K_{(298 K)}=5.9 \times 10^{55}\)

Solution

Use the value of the equilibrium constant to determine whether the equilibrium mixture will contain essentially only products, essentially only reactants, or significant amounts of both.

Only system 4 has \(K \gg 10^3\), so at equilibrium it will consist of essentially only products.
System 2 has \(K \ll 10^{−3}\), so the reactants have little tendency to form products under the conditions specified; thus, at equilibrium the system will contain essentially only reactants.
Both systems 1 and 3 have equilibrium constants in the range \(10^3 \ge K \ge 10^{−3}\), indicating that the equilibrium mixtures will contain appreciable amounts of both products and reactants.

Exercise \(\PageIndex{2}\)

Hydrogen and nitrogen react to form ammonia according to the following balanced chemical equation:

\[3H_{2(g)}+N_{2(g)} \rightleftharpoons 2NH_{3(g)} \nonumber \]

Values of the equilibrium constant at various temperatures were reported as

\(K_{25°C} = 3.3 \times 10^8\),
\(K_{177°C} = 2.6 \times 10^3\), and
\(K_{327°C} = 4.1\).

At which temperature would you expect to find the highest proportion of \(H_2\) and \(N_2\) in the equilibrium mixture?
At which temperature would you expect to find the highest proportion of ammonia in the equilibrium mixture?

Answer

a. 327°C, where \(K\) is smallest

b. 25°C

Reaction Quotient

The reaction quotient, \(Q\), is used when questioning if we are at equilibrium. The calculation for \(Q\) is exactly the same as for \(K\) but we can only use \(K\) when we know we are at equilibrium. Comparing \(Q\) and \(K\) allows the direction of the reaction to be predicted.

\(Q\) = \(K\) equilibrium
\(Q\) < \(K\) reaction proceeds to the right to form more products and decrease amount of reactants so value of \(Q\) will increase
\(Q\) > \(K\) reaction proceeds to the left to form more reactants and decrease amount of products so value of \(Q\) will decrease

Key Takeaway

As a chemical change proceeds, the quantities of the reactants/products will decrease, and those of the products/reactants will increase. Eventually the reaction slows down and the composition of the system stops changing. At this point the reaction is in its equilibrium state, and no further change in composition will occur as long as the system is left undisturbed.

Contributors and Attributions

Allison Soult, Ph.D. (Department of Chemistry, University of Kentucky)