Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

23.5: Standard Hydrogen Electrode

Last updated

Mar 21, 2025
Save as PDF
- 23.4: Electrical Potential
- 23.6: Calculating Standard Cell Potentials

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

It's a human tendency to compare ourselves to someone else. Can I run faster than you? Am I taller than my dad?—these are relative comparisons that don't provide much useful data. When we use a standard for our comparisons, one thing is much more comparable to another. One meter is the same distance everywhere in the world, so a 100 meter track in one country is exactly the same distance as a 100 meter track in another country—this is a universal basis for the comparison of a running time, for example.

Standard Hydrogen Electrode

The activity series allows us to predict the relative reactivity of different materials when used in oxidation-reduction processes. We also know we can create electric current by a combination of chemical processes. But how do we predict the expected amount of current that will flow through the system? We measure this flow as voltage (an electromotive force or potential difference).

In order to do this, we need some way of comparing the extent of electron flow in various chemical systems. The best way to do this is to have a baseline that we use—a standard that everything can be measured against. For determination of half-reaction current flows and voltages, we use the standard hydrogen electrode. The figure below illustrates this electrode. A platinum wire conducts the electricity through the circuit. The wire is immersed in a $1.0 \: \text{M}$ strong acid solution and $\ce{H_2}$ gas is bubbled in at a pressure of one atmosphere and a temperature of $25^\text{o} \text{C}$ . The half-reaction at this electrode is $\ce{H_2} \rightarrow 2 \ce{H^+} + 2 \ce{e^-}$ .

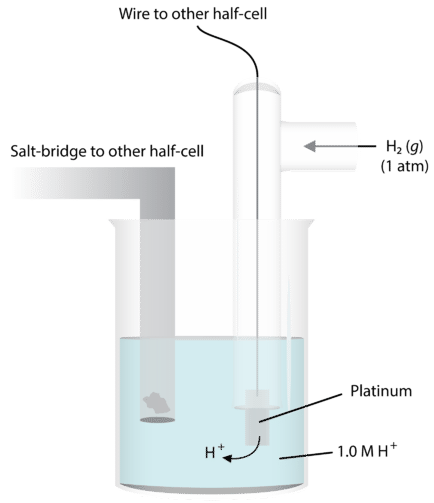
Diagram of an electrochemical cell with a beaker containing a platinum electrode in 1.0 M H⁺ solution. A glass tube with H₂ gas is connected, and a wire and salt bridge lead to another half-cell. — Figure $\PageIndex{1}$ : The standard hydrogen electrode.

Under these conditions, the potential for the hydrogen reduction is defined as exactly zero. We call this $E^0$ , the standard reduction potential.

We can then use this system to measure the potentials of other electrodes in the half-cell. A metal and one of its salts (sulfate is often used) is in the second half-cell. We will use zinc as our example (see figure below).

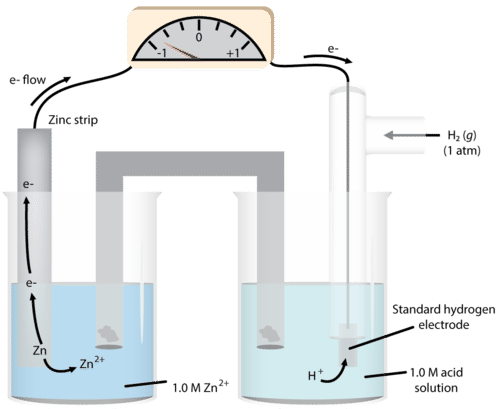
Diagram of a galvanic cell featuring a zinc strip, hydrogen electrode, and voltmeter. Zinc ions (Zn²⁺) are in solution at 1.0 M concentration, with hydrogen gas at 1 atm. Arrows show electron flow. — Figure $\PageIndex{2}$ : The standard hydrogen half-cell paired with a zinc half-cell.

As we observe the reaction, we notice that the mass of solid zinc decreases during the course of the reaction. This suggests that the reaction occurring in that half-cell is:

$\ce{Zn} \left( s \right) \rightarrow \ce{Zn^{2+}} \left( aq \right) + 2 \ce{e^-}\nonumber$

So, we have the following process occurring in the cell:

$\begin{align*} &\ce{Zn} \left( s \right) \rightarrow \ce{Zn^{2+}} \left( aq \right) + 2 \ce{e^-} \: \left( \text{anode - oxidation} \right) \\ &2 \ce{H^+} \left( aq \right) + 2 \ce{e^-} \rightarrow \ce{H_2} \left( g \right) \: \left( \text{cathode - reduction} \right) \end{align*}\nonumber$

The measured cell voltage is 0.76 volts (abbreviated as $\text{V}$ ).

We define the standard emf (electromotive force) of the cell as:

$\begin{align*} E^0_\text{cell} &= E^0_\text{cathode} - E^0_\text{anode} \\ 0.76 \: \text{V} &= 0 - E^0_{\ce{Zn} \: \text{cell}} \\ E^0_{\ce{Zn} \: \text{cell}} &= -0.76 \: \text{V} \end{align*}\nonumber$

We can do the same determination with a copper cell (figure below).

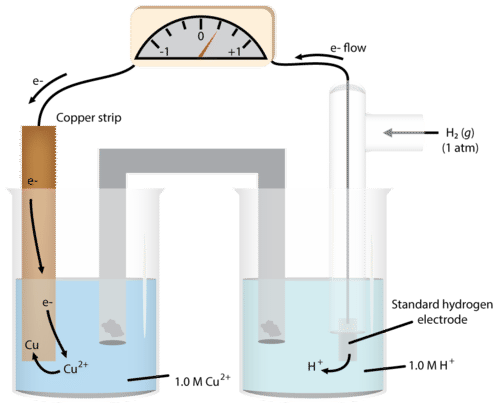
Diagram of a galvanic cell with a copper strip in a Cu²⁺ solution and a standard hydrogen electrode in an acidic solution. Arrows indicate electron flow. A salt bridge connects the two beakers. — Figure $\PageIndex{3}$ : The standard hydrogen half-cell paired with a copper half-cell.

As we run the reaction, we see the mass of the copper increases, so we write the half-reaction:

$\ce{Cu^{2+}} + 2 \ce{e^-} \rightarrow \ce{Cu}\nonumber$

This makes the copper electrode the cathode. We now have the two half-reactions:

$\begin{align*} &\ce{H_2} \rightarrow 2 \ce{H^+} + 2 \ce{e^-} \: \left( \text{anode} \right) \\ &\ce{Cu^{2+}} + 2 \ce{e^-} \rightarrow \ce{Cu} \: \left( \text{cathode} \right) \end{align*}\nonumber$

We determine the $E^0$ for the system to be $0.34 \: \text{V}$ .

Again,

$\begin{align*} E^0_\text{cell} &= E^0_\text{cathode} - E^0_\text{anode} \\ 0.34 \: \text{V} &= E^0_\text{copper} - 0 \end{align*}\nonumber$

So, copper potential $= 0.34 \: \text{V}$ .

Now, we want to build a system in which both zinc and copper are involved. We know from the activity series that zinc will be oxidized and copper reduced, so we can use the values at hand:

$E^0_\text{cell} = 0.34 \: \text{V} \: \left( \text{copper} \right) - \left( -0.76 \: \text{V} \: \text{zinc} \right) = 1.10 \: \text{volts for the cell}\nonumber$

Summary

The standard hydrogen electrode is used for determination of half-reaction current flows and voltages.
The structure of the standard hydrogen electrode is described.
Examples of using the standard hydrogen electrode to determine reduction potentials are given.

Standard Hydrogen Electrode

Summary

Support Center

How can we help?