1.4: Significant Figures

Significant figures are related to errors associated with the measured numbers. It is important to understand the significant figures because when calculations are made using numbers with errors, the answer cannot have less error than the error in any original number. The answer needs correction for the significant figures.

Precision and accuracy

The measured numbers have two types of errors, systematic and random errors, that determine the accuracy and precision of the measured number, as illustrated in Fig. 1.4.1.

Figure \(\PageIndex{1}\): Representation of high accuracy with less precision (left) and low accuracy with high precision (right). Source: DarkEvil / Public domain

Systematic errors

Systematic errors are constant, i.e., they have the same value in every measurement. For example, meter rod is a little short or a little long than a meter, it will introduce a systematic error. Systematic errors usually happen due to inaccurate calibration of the measuring instrument. The systematic errors determine how much the measured value differs from the actual value.

Random errors

Random errors are the statistical variability of the measured number. Random errors vary from one observation to another. Random errors cancel out if many measurements are taken and averaged. Scientific measurements are usually taken at least in triplicate and averaged to minimize random errors. The random errors determine how close the repeat measured numbers are to each other.

Accuracy

Accuracy or trueness of the measurement is defined as how close the average value is to the actual value.

The closer the average is to the actual value, the more accurate or true it is, as illustrated in Fig. 1.4.1. The trueness depends on systematic errors, i.e., less systematic error, more accurate the average.

Precision

Precision is defined as how close the individual measurements are to each other.

The closer the individual values are to each other, the more precise the measurement is, irrespective of whether it is accurate or not, as illustrated in Fig. 1.4.1. Precision depends on random errors, i.e., more substantial random errors mean less precision.

Exact and inexact number

There are two types of numbers, count numbers that are exact and measured numbers that are inexact.

If the value is a counted number, it is an exact number.

That is, there is no error in it. For example, a purchase of one dozen oranges contains exactly 12 nos of oranges; it can not be 11.5 or 12.5.

Inexact numbers and error range

When a value is measured, it comes with an error of measurement.

A measured number with an error is called an inexact number.

For example, when the same one dozen oranges are purchased by mass, the balance may read it 1572.6 g, or 1573 g, or 1570 g, depending on whether the smallest digit that the balance displays is 0.1g, 1 g, or 10 g. Suppose the balance is accurate to 1 g and reports the mass 1573 g; the actual mass may be anywhere in the range of 1572.5g-to-1573.4g. The smallest measured digit, i.e., the number in one's place, in this case, is an estimated number associated with an error. By convention, the estimated digit has ±1 errors associated with it. For example, the above-mentioned measured numbers are reported in science as 1572.6 g ± 0.1 g, 1573 g ± 1 g, or 1570 g ± 10 g, respectively. The estimated digits are shown in bold fonts in the examples.

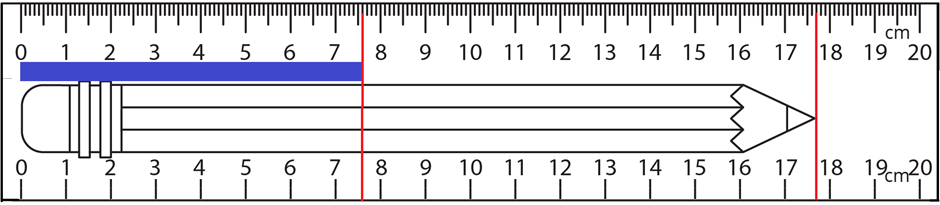
The smallest digit in the display of digital instruments is an estimated number. In measurement using instruments that do not have a digital display, the smallest digit marked on the instrument plus one digit less than the minimum marked digit is added to the reported value. The smallest reported digit is an estimated digit. For example, the length of the pencil in Fig 1.4.2 is reported as 17.7 cm using the ruler on the bottom, where 17 includes the smallest digit marked on the ruler, and the last digit, i.e., 0.7 is an estimated digit. By convention, the error range in this value is shown as 17.7 ± 0.1. The same length is 17.70 cm using the ruler on the top in Fig. 1.4.2l, where 17.7 includes the smallest digit marked on the ruler, and the last reported digit, i.e., 0, is an estimated digit. By convention, the error range in this value is shown as 17.70 ± 0.01. The estimated digits are marked in bold fonts.

Figure \(\PageIndex{1}\): Illustration of measurements that yield inexact numbers. The length of a blue rectangle is 7.60 ± 0.01 cm by using a more accurate ruler on the top and 7.6 ±0.1 cm by using a less accurate ruler on the bottom. The estimated digit is marked in bold fonts.

Rules to determine the significant figures in measured numbers

Significant figures

All the digits reported in the measured value, including the estimated digit, are significant figures (SF).

For example, 1572.6 g, 1573 g, and 1570 g have significant figures of 5, 4, and 3, respectively.

Caution

Note that zero in the last reading 1570g is not significant; it is a placeholder zero that is needed to place the estimated digit 7 at tens place.

It is crucial to find significant figures in measured numbers because, when they are used in calculations, the answer cannot have less error than the maximum error in any measured number used in the calculation. The rules to determine the significant numbers in a measured number are the following.

1. All non-zero digits are significant, e.g., 1572 has 4 SFs. The zeros may or may not be significant. In the following examples, the zeros in bold fonts are nonsignificant.
2. Zeros between non-zero digits are significant, e.g., 1305.6 has 5 SFs.
3. Leading zeros are not significant, e.g., 0.0134 has 3 SFs.
4. Trailing zeros are not significant if there is no decimal point present, e.g., 1570 has 3 SFs. Trailing zeros are significant if the decimal point is present, e.g., 1570. has 4 SFs because the decimal point is present. Similarly, 0.0124 has 3 SFs, but 0.01240 has 4 SFs because the decimal point is present.
5. Confusion arises when more than one trailing zeros and the decimal point is absent. For example, 1500 g has 2 SFs by convention, but if the balance was accurate to 10 g, one of the zero was an estimated digit and was significant. Converting the number to a scientific notation resolves this issue. The coefficient part of the scientific notation shows all the significant figures in the measurement. For example, the number 1500 g, if shown in scientific notation as 1.5 x 10³ has 2 SFs, but the same number shown as 1.50 x 10³ has 3 SFs.

Rounding the calculated answer involving inexact numbers

When inexact numbers are used in calculations, the answer needs to be rounded to an appropriate number of significant figures, determined by the following rules.

Rules of rounding

1. A number is rounded by keeping the larger digits equal to significant figures and dropping or replacing the remaining smaller digits with placeholder zeros. The placeholder zeros are in bold fonts in the following examples. For example, 13543 becomes 13500 when rounded to three significant.
2. If the largest digit dropped is 4 or less than 4, it is simply dropped. For example, 23145 becomes 23100, when rounded to three significant figures.
3. If the largest digit dropped is 5 or more than 5, then the smallest digit retained is increased by one. For example, 13543 becomes 14000 when rounded into two significant figures.

Rules for determining the significant figures in a calculated answer

In the following rules, the track of significant figures that dictate the significant figures in the answer is kept by using bold fonts.

1. In addition and subtraction, the answer has the same number of decimal places as the number with the smallest number of decimal places in the original numbers. For example, 13.2 + 12.252 = 25.452 is rounded to 25.5 to keep one decimal place.
2. In multiplication and division, the answer has the same number of significant figures as the original number with the smallest number of significant figures. For example, 1.35 x 2.1 = 2.835 is rounded to 2.8.

Note

If mathematical operations are performed in a series of steps, keep track of the significant figures but do not round off intermediate answers. Carry as many digits as possible from the intermediate answers to the next calculation step. Round off the final answer following the above rules. For example, (13.2 + 12.252) x (1.35 x 2.1) = 25.452 x 2.835 = 72.15642 is round to 72 in agreement with 2.835 that should have been rounded to 2.8 in a one-step calculation. Rounding the intermediate answers will lead to incorrect final answer of 71 instead of more correct 72, i.e. (13.2 + 12.252) x (1.35 x 2.1) = 25.5 x 2.8 = 71

Caution

Exact numbers have an unlimited number of significant figures, which means they do not restrict the significant figures in the calculated answer.

Example \(\PageIndex{1}\)

If 12 oranges weigh 1572.6 g calculate the mass of 1 orange in grams?

Solution

\begin{equation}
1572.6 \mathrm{~g} / 12=131.05 \mathrm{~g}\nonumber
\end{equation}

Explanation: The answer has 5 SFs because 12 is a counted number and exact. The only inexact number in the calculation that dictates the significant figures in the solution is 1572.6, which has 5 SFs.

Example \(\PageIndex{2}\)

One dozen oranges were were sold 11 times. Calculate the total oranges sold?

Solution

\begin{equation}
12 \times 11=132 \text { oranges }\nonumber
\end{equation}

Explanation: The answer is not rounded because both the numbers in the calculation are exact, so the answer is also exact with unlimited significant figures.