11.5: Radioactive Half-Life

Learning Objectives

• Define half-life.
• Determine the amount of radioactive substance remaining after a given number of half-lives.
• Describe common radiometric carbon-14 dating technique.

Whether or not a given isotope is radioactive is a characteristic of that particular isotope. Some isotopes are stable indefinitely, while others are radioactive and decay through a characteristic form of emission. As time passes, less and less of the radioactive isotope will be present, and the level of radioactivity decreases. An interesting and useful aspect of radioactive decay is half life (t_1/2), which is the amount of time it takes for one-half of a radioactive isotope to decay. The half-life of a specific radioactive isotope is constant; it is unaffected by conditions and is independent of the initial amount of that isotope.

Each radioactive nuclide has a characteristic, constant half-life (t_1/2), the time required for half of the atoms in a sample to decay. An isotope’s half-life allows us to determine how long a sample of a useful isotope will be available, and how long a sample of an undesirable or dangerous isotope must be stored before it decays to a low-enough radiation level that is no longer a problem.

For example, cobalt-60 source, since half of the \(\ce{^{60}_{27}Co}\) nuclei decay every 5.27 years, both the amount of material and the intensity of the radiation emitted is cut in half every 5.27 years. (Note that for a given substance, the intensity of radiation that it produces is directly proportional to the rate of decay of the substance and the amount of the substance.) Thus, a cobalt-60 source that is used for cancer treatment must be replaced regularly to continue to be effective.

Figure \(\PageIndex{1}\): For cobalt-60, which has a half-life of 5.27 years, 50% remains after 5.27 years (one half-life), 25% remains after 10.54 years (two half-lives), 12.5% remains after 15.81 years (three half-lives), and so on. (CC BY 4.0; OpenStax)

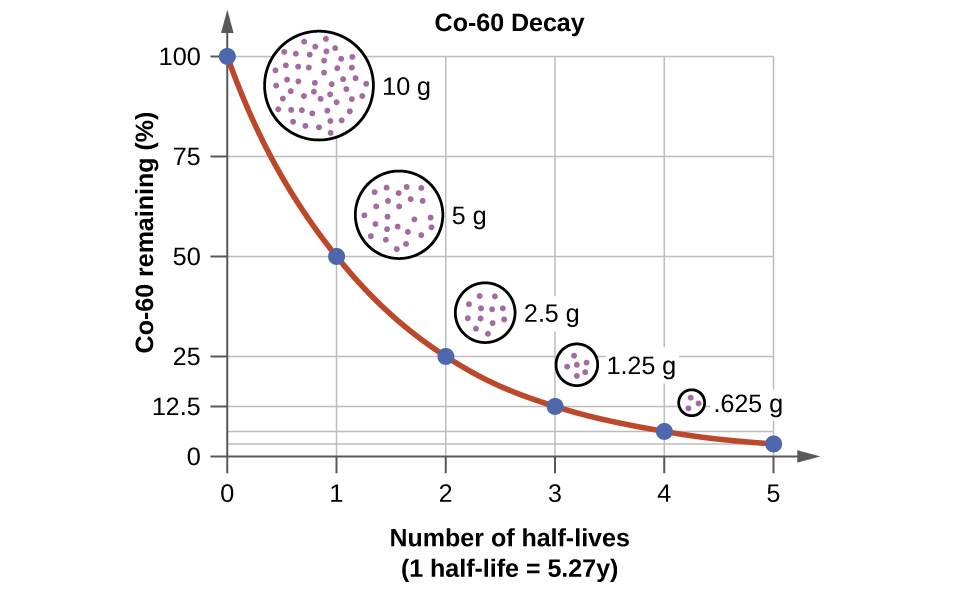
We can determine the amount of a radioactive isotope remaining after a given number half-lives by using the following expression:

\[\text{amount remaining} = \text{initial amount} \times \left ( \frac{1}{2} \right )^{n}\]

where \(n\) is the number of half-lives. This expression works even if the number of half-lives is not a whole number.

Example \(\PageIndex{1}\): Fluorine-20

The half-life of fluorine-20 is 11.0 s. If a sample initially contains 5.00 g of fluorine-20, how much remains after 44.0 s?

Solution

If we compare the time that has passed to the isotope's half-life, we note that 44.0 s is exactly 4 half-lives, so using the previous expression, n = 4. Substituting and solving results in the following:

\[\begin{align*} \text{amount remaining} &= 5.00\,g \times \left ( \frac{1}{2} \right )^{4} \\[4pt] & =\: 5.00\,g\times \left ( \frac{1}{16} \right ) \\[4pt] &= 0.313\,g \end{align*}\]

Less than one-third of a gram of fluorine-20 remains.

Exercise \(\PageIndex{1}\): Titanium-44

The half-life of titanium-44 is 60.0 y. A sample of titanium contains 0.600 g of titanium-44. How much remains after 240.0 y?

Answer

0.0375 g

Half-lives of isotopes range from fractions of a microsecond to billions of years. Table \(\PageIndex{1}\) - Half-Lives of Various Isotopes, lists the half-lives of some isotopes.

Table \(\PageIndex{1}\) Half-Lives of Various Isotopes

Isotope	Half-Life
^3H	12.3 y
^14C	5730 y
^40K	1.26 × 10^9 y
^51Cr	27.70 d
^90Sr	29.1 y
^131I	8.04 d
^222Rn	3.823 d
^235U	7.04 × 10^8 y
^238U	4.47 × 10^9 y
^241Am	432.7 y
^248Bk	23.7 h
^260Sg	4 ms

Chemistry Is Everywhere: Radioactive Elements in the Body

You may not think of yourself as radioactive, but you are. A small portion of certain elements in the human body are radioactive and constantly undergo decay. Most of the radioactivity in the human body comes from potassium-40 and carbon-14. Potassium and carbon are two elements that we absolutely cannot live without, so unless we can remove all the radioactive isotopes of these elements, there is no way to escape at least some radioactivity. There is debate about which radioactive element is more problematic. There is more potassium-40 in the body than carbon-14, and it has a much longer half-life. Potassium-40 also decays with about 10 times more energy than carbon-14, making each decay potentially more problematic. However, carbon is the element that makes up the backbone of most living molecules, making carbon-14 more likely to be present around important molecules, such as proteins and DNA molecules. Most experts agree that while it is foolhardy to expect absolutely no exposure to radioactivity, we can and should minimize exposure to excess radioactivity.

Radiometric Dating

Several radioisotopes have half-lives and other properties that make them useful for purposes of “dating” the origin of objects such as archaeological artifacts, formerly living organisms, or geological formations. The radioactivity of carbon-14 provides a method for dating objects that were a part of a living organism. This method of radiometric dating, which is also called radiocarbon dating or carbon-14 dating, is accurate for dating carbon-containing substances that are up to about 30,000 years old, and can provide reasonably accurate dates up to a maximum of about 50,000 years old.

Naturally occurring carbon consists of three isotopes: \(\ce{^{12}_6C}\), which constitutes about 99% of the carbon on earth; \(\ce{^{13}_6C}\), about 1% of the total; and trace amounts of \(\ce{^{14}_6C}\). Carbon-14 forms in the upper atmosphere by the reaction of nitrogen atoms with neutrons from cosmic rays in space:

\[\ce{^{14}_7N + ^1_0n⟶ ^{14}_6C + ^1_1H}\nonumber \]

All isotopes of carbon react with oxygen to produce CO₂ molecules. The ratio of \(\ce{^{14}_6CO2}\) to \(\ce{^{12}_6CO2}\) depends on the ratio of \(\ce{^{14}_6CO}\) to \(\ce{^{12}_6CO}\) in the atmosphere. The natural abundance of \(\ce{^{14}_6CO}\) in the atmosphere is approximately 1 part per trillion; until recently, this has generally been constant over time, as seen is gas samples found trapped in ice. The incorporation of \(\ce{^{14}_6C ^{14}_6CO2}\) and \(\ce{^{12}_6CO2}\) into plants is a regular part of the photosynthesis process, which means that the \(\ce{^{14}_6C: ^{12}_6C}\) ratio found in a living plant is the same as the \(\ce{^{14}_6C: ^{12}_6C}\) ratio in the atmosphere. But when the plant dies, it no longer traps carbon through photosynthesis. Because \(\ce{^{12}_6C}\) is a stable isotope and does not undergo radioactive decay, its concentration in the plant does not change. However, carbon-14 decays by β emission with a half-life of 5730 years:

\[\ce{^{14}_6C⟶ ^{14}_7N + ^0_{-1}e}\nonumber \]

Thus, the \(\ce{^{14}_6C: ^{12}_6C}\) ratio gradually decreases after the plant dies. The decrease in the ratio with time provides a measure of the time that has elapsed since the death of the plant (or other organism that ate the plant). Figure \(\PageIndex{2}\) visually depicts this process.

Figure \(\PageIndex{2}\): Along with stable carbon-12, radioactive carbon-14 is taken in by plants and animals, and remains at a constant level within them while they are alive. After death, the C-14 decays and the C-14:C-12 ratio in the remains decreases. Comparing this ratio to the C-14:C-12 ratio in living organisms allows us to determine how long ago the organism lived (and died). (CC BY 4.0; OpenStax)

For example, with the half-life of \(\ce{^{14}_6C}\) being 5730 years, if the \(\ce{^{14}_6C : ^{12}_6C}\) ratio in a wooden object found in an archaeological dig is half what it is in a living tree, this indicates that the wooden object is 5730 years old. Highly accurate determinations of \(\ce{^{14}_6C : ^{12}_6C}\) ratios can be obtained from very small samples (as little as a milligram) by the use of a mass spectrometer.

Key Takeaways

• Natural radioactive processes are characterized by a half-life, the time it takes for half of the material to decay radioactively.
• The amount of material left over after a certain number of half-lives can be easily calculated.