9.5: The Effect of Pressure on Solubility - Henry’s Law
- Page ID
- 258796
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe how pressure affects concentration of a solute in a solution.
Pressure has very little effect on the solubility of solids or liquids, but has a significant effect on the solubility of gases. Gas solubility increases as the partial pressure of a gas above the liquid increases. Suppose a certain volume of water is in a closed container with the space above it occupied by carbon dioxide gas at standard pressure. Some of the \(\ce{CO_2}\) molecules come into contact with the surface of the water and dissolve into the liquid. Now suppose that more \(\ce{CO_2}\) is added to the space above the container, causing a pressure increase. In this case, more \(\ce{CO_2}\) molecules are in contact with the water and so more of them dissolve. Thus, the solubility increases as the pressure increases. As with a solid, the \(\ce{CO_2}\) that is undissolved reaches an equilibrium with the dissolved \(\ce{CO_2}\), represented by the equation:
\[\ce{CO_2} \left( g \right) \rightleftharpoons \ce{CO_2} \left( aq \right)\nonumber \]
At equilibrium, the rate of gaseous \(\ce{CO_2}\) dissolution is equal to the rate of dissolved \(\ce{CO_2}\) coming out of the solution.
When carbonated beverages are packaged, they are done so under high \(\ce{CO_2}\) pressure so that a large amount of carbon dioxide dissolves in the liquid. When the bottle is open, the equilibrium is disrupted because the \(\ce{CO_2}\) pressure above the liquid decreases. Immediately, bubbles of \(\ce{CO_2}\) rapidly exit the solution and escape out of the top of the open bottle, see Figure \(\PageIndex{1}\). The amount of dissolved \(\ce{CO_2}\) decreases. If the bottle is left open for an extended period of time, the beverage becomes "flat" as more and more \(\ce{CO_2}\) comes out of the liquid.

The relationship of gas solubility to pressure is described by Henry's law, named after English chemist William Henry (1774-1836). Henry's Law states that the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas above the liquid. Henry's law can be written as follows:
\[\frac{C_1}{P_1} = \frac{C_2}{P_2} = k \nonumber \]
\(C_1\) and \(P_1\) are the concentration and the pressure at an initial set of conditions; \(C_2\) and \(P_2\) are the concentration and pressure at another changed set of conditions; \(k\) is a constant at a constant temperature. The solubility of a gas is typically reported in \(\text{g/L}\).
The solubility of a certain gas in water is \(0.745 \: \text{g/L}\) at standard pressure. What is its solubility when the pressure above the solution is raised to \(4.50 \: \text{atm}\)? The temperature is constant at \(20^\text{o} \text{C}\).
Solution
Step 1: List the known quantities and plan the problem.
Known
- \(C_1 = 0.745 \: \text{g/L}\)
- \(P_1 = 1.00 \: \text{atm}\)
- \(P_2 = 4.50 \: \text{atm}\)
Unknown
Substitute into Henry's law and solve for \(C_2\).
Step 2: Solve.
\[C_2 = \frac{C_1 \times P_2}{P_1} = \frac{0.745 \: \text{g/L} \times 4.50 \: \text{atm}}{1.00 \: \text{atm}} = 3.35 \: \text{g/L}\nonumber \]
Step 3: Think about your result.
The solubility is increased to 4.5 times its original value, according to the direct relationship.
Exposing a 100.0 mL sample of water at 0 °C to an atmosphere containing a gaseous solute at 20.26 kPa (152 torr) resulted in the dissolution of 1.45 × 10−3 g of the solute. Use Henry’s law to determine the solubility of this gaseous solute when its pressure is 101.3 kPa (760 torr).
- Answer
-
7.25 × 10−3 g in 100.0 mL or 0.0725 g/L
Decompression sickness (DCS), or “the bends,” is an effect of the increased pressure of the air inhaled by scuba divers when swimming underwater at considerable depths. In addition to the pressure exerted by the atmosphere, divers are subjected to additional pressure due to the water above them, experiencing an increase of approximately 1 atm for each 10 m of depth. Therefore, the air inhaled by a diver while submerged contains gases at the corresponding higher ambient pressure, and the concentrations of the gases dissolved in the diver’s blood are proportionally higher per Henry’s law.
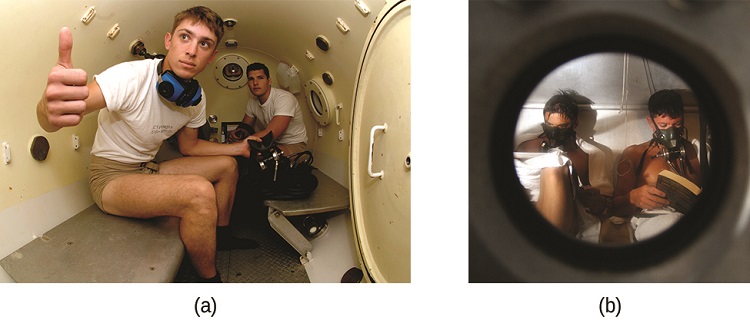
As the diver ascends to the surface of the water, the ambient pressure decreases and the dissolved gases becomes less soluble. If the ascent is too rapid, the gases escaping from the diver’s blood may form bubbles that can cause a variety of symptoms ranging from rashes and joint pain to paralysis and death. To avoid DCS, divers must ascend from depths at relatively slow speeds (10 or 20 m/min) or otherwise make several decompression stops, pausing for several minutes at given depths during the ascent. When these preventive measures are unsuccessful, divers with DCS are often provided hyperbaric oxygen therapy in pressurized vessels called decompression (or recompression) chambers (Figure \(\PageIndex{4}\)).

