8.9: Avogadro’s Law - The Relation between Volume and Molar Amount
- Page ID
- 258789
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe the relationship between the amount and volume of a gas, Avogadro's Law.
- Define the conditions of standard temperature and pressure.
The Relationship between Amount and Volume: Avogadro's Law
We can demonstrate the relationship between the volume and the amount of a gas by filling a balloon; as we add more gas, the balloon gets larger. The specific quantitative relationship was discovered by the Italian chemist Amedeo Avogadro, who recognized the importance of Gay-Lussac’s work on combining volumes of gases. In 1811, Avogadro postulated that, at the same temperature and pressure, equal volumes of gases contain the same number of gaseous particles (Figure \(\PageIndex{1}\)). This is the historic “Avogadro’s hypothesis.”
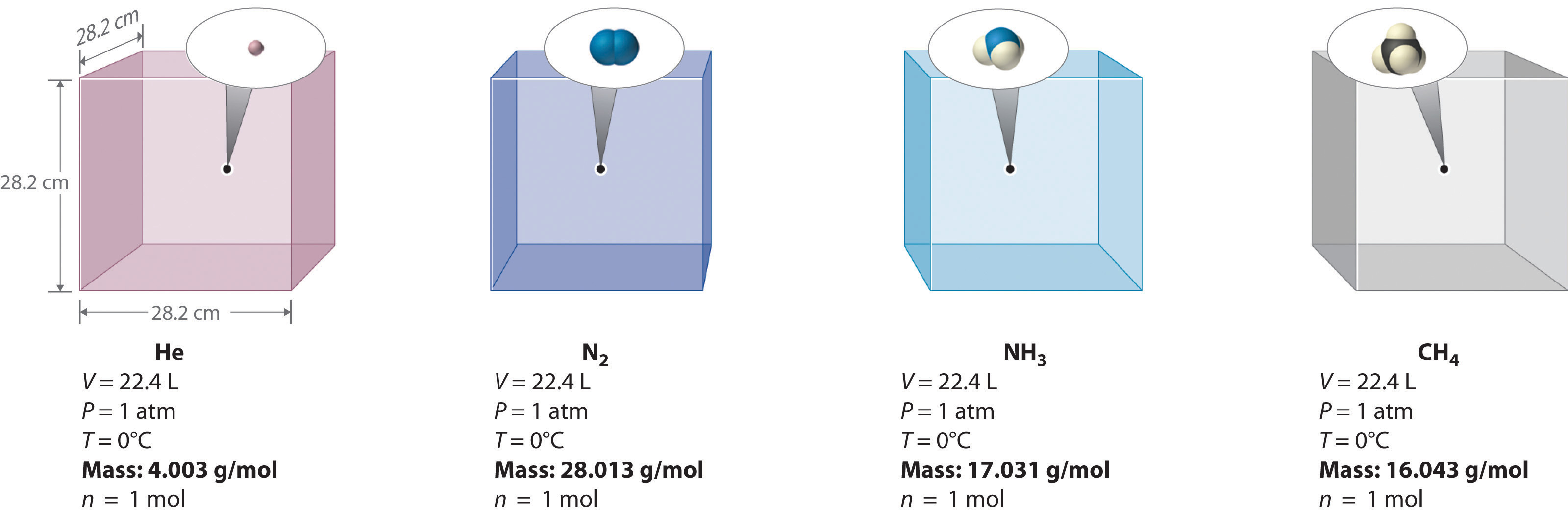
Because the number of particles is related to the number of moles (1 mol = 6.022 × 1023 particles), Avogadro's law essentially states that equal volumes of different gases, at the same temperature and pressure, contain the same amount (moles, particles) of gas. At constant temperature and pressure, the volume (V) of a sample of gas is directly proportional to the number of moles (n) of gas in the sample. Stated mathematically,
\[V\propto n\ce{\:or\:} V=k×n\ce{\:or\:} \dfrac{V}{n}=k \nonumber \]
where \(\propto\) means “is proportional to,” and k is a proportionality constant that is the same for all gases.
In terms of two sets of data: \(\dfrac{V_1}{n_1}=\dfrac{V_2}{n_2}\).
This relationship is valid for most gases at relatively low pressures, but deviations from strict linearity are observed at elevated pressures. Mathematical relationships can also be determined for the other variable pairs, such as P versus n, and n versus T.
Visit this interactive PhET simulation to investigate the relationships between pressure, volume, temperature, and amount of gas. Use the simulation to examine the effect of changing one parameter on another while holding the other parameters constant (as described in the preceding sections on the various gas laws).
Standard Temperature and Pressure
It should be obvious by now that some physical properties of gases depend strongly on the conditions. What we need is a set of standard conditions so that properties of gases can be properly compared to each other. Standard Temperature and Pressure (STP) is defined as exactly 100 kPa of pressure (0.986 atm) and 273 K (0°C). For simplicity, we will use 1 atm as standard pressure. Defining STP allows us to more directly compare the properties of gases that differ from one another.
One property shared among gases is a molar volume. The molar volume is the volume of 1 mol of a gas. At STP, the molar volume of a gas can be easily determined by using the ideal gas law:
\[(1\, atm)V=(1\, mol) \left(0.08205\dfrac{L.atm}{mol.K}\right)(273\, K)\nonumber \]
All the units cancel except for L, the unit of volume. So V = 22.4 L
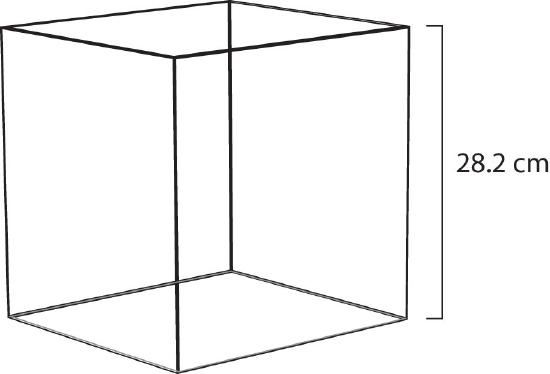
Note that we have not specified the identity of the gas; we have specified only that the pressure is 1 atm and the temperature is 273 K. This makes for a very useful approximation: any gas at STP has a volume of 22.4 L per mole of gas; that is, the molar volume at STP is 22.4 L/mol (Figure \(\PageIndex{1}\)). This molar volume makes a useful conversion factor in stoichiometry problems if the conditions are at STP. If the conditions are not at STP, a molar volume of 22.4 L/mol is not applicable. However, if the conditions are at STP, the combined gas law can be used to calculate what the volume of the gas would be if at STP; then the 22.4 L/mol molar volume can be used.
How many moles of \(\ce{Ar}\) are present in 38.7 L at STP?
Solution
We can use the molar volume, 22.4 L/mol, as a conversion factor, but we need to reverse the fraction so that the L units cancel and mol units are introduced. It is a one-step conversion:
\[38.7\, \cancel{L}\times \frac{1\, mol}{22.4\cancel{L}}=1.73\, mol\nonumber \]
What volume does 4.87 mol of \(\ce{Kr}\) have at STP?
- Answer
-
109 L
What volume of \(\ce{H2}\) is produced at STP when 55.8 g of \(\ce{Zn}\) metal react with excess \(\ce{HCl}\)?
\[\ce{Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g)} \nonumber \]
Solution
This is a stoichiometry problem with a twist: we need to use the molar volume of a gas at STP to determine the final answer. The first part of the calculation is the same as in a previous example:
\[55.8\cancel{g\, Zn}\times \frac{1\cancel{mol\, Zn}}{65.41\cancel{g\, Zn}}\times \frac{1\, mol\, H_{2}}{1\cancel{mol\, Zn}}=0.853\, H_{2}\nonumber \]
Now we can use the molar volume, 22.4 L/mol, because the gas is at STP:
\[0.853\cancel{mol\, H_{2}}\times \frac{22.4\, L}{1\cancel{mol\, H_{2}}}=19.1\, L\, H_{2}\nonumber \]
Alternatively, we could have applied the molar volume as a third conversion factor in the original stoichiometry calculation.
What volume of \(\ce{HCl}\) is generated if 3.44 g of \(\ce{Cl2}\) are reacted at STP?
\[\ce{H2(g) + Cl2(g) → 2HCl(g)} \nonumber \]
- Answer
-
2.17 L
Summary
- Avogadro's law states that the volume of gas is directly proportional to the number of moles of gas.
- Standard temperature and pressure (STP) are a useful set of benchmark conditions to compare other properties of gases.
- At STP, gases have a volume of 22.4 L per mole.

