8.5: Boyle’s Law - The Relation between Volume and Pressure

Learning Objectives

• Define the relationship between gas volume and pressure, Boyle's Law.
• Use Boyle's Law to calculate changes in pressure or volume of a gas.

When seventeenth-century scientists began studying the physical properties of gases, they noticed some simple relationships between some of the measurable properties of the gas. Take pressure (P) and volume (V), for example. Scientists noted that for a given amount of a gas (usually expressed in units of moles [n]), if the temperature (T) of the gas was kept constant, pressure and volume were related: As one increases, the other decreases. As one decreases, the other increases. We say that pressure and volume are inversely related.

There is more to it, however: pressure and volume of a given amount of gas at constant temperature are numerically related. If you take the pressure value and multiply it by the volume value, the product is a constant (k) for a given amount of gas at a constant temperature:

\[P \times V=k\; (at\; constant\; n\; and\; T)\nonumber \]

If either volume or pressure changes while amount and temperature stay the same, then the other property must change so that the product of the two properties still equals that same constant. That is, if the original conditions are labeled P₁ and V₁ and the new conditions are labeled P₂ and V₂, we have

\[P_{1}V_{1}= k = P_{2}V_{2}\; \nonumber \]

where the properties are assumed to be multiplied together. Leaving out the middle part, we have simply

\[P_{1}V_{1}= P_{2}V_{2}\; (at\; constant\; n\; and\; T)\nonumber \]

This equation is an example of a gas law. A gas law is a simple mathematical formula that allows you to model, or predict, the behavior of a gas. This particular gas law is called Boyle's law, after the English scientist Robert Boyle, who first announced it in 1662. Figure \(\PageIndex{1}\) shows two representations of how Boyle's law works.

Figure \(\PageIndex{1}\): Boyle's Law. A piston having a certain pressure and volume (left piston) will have half the volume when its pressure is twice as much (right piston). One can also plot P versus V for a given amount of gas at a certain temperature; such a plot will look like the graph on the right.

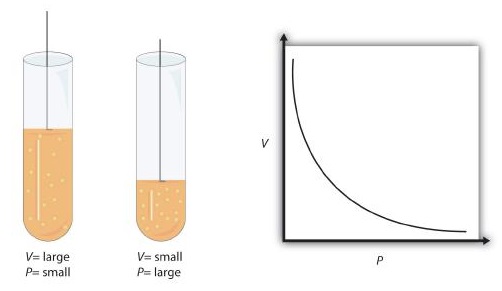
Boyle's law is an example of a second type of mathematical problem we see in chemistry—one based on a mathematical formula. Tactics for working with mathematical formulas are different from tactics for working with conversion factors. First, most of the questions you will have to answer using formulas are word-type questions, so the first step is to identify what quantities are known and assign them to variables. Second, in most formulas, some mathematical rearrangements (i.e., algebra) must be performed to solve for an unknown variable. The rule is that to find the value of the unknown variable, you must mathematically isolate the unknown variable by itself and in the numerator of one side of the equation. Finally, units must be consistent. For example, in Boyle's law there are two pressure variables; they must have the same unit. There are also two volume variables; they also must have the same unit. In most cases, it won't matter what the unit is, but the unit must be the same on both sides of the equation.

Example \(\PageIndex{1}\)

A sample of gas has an initial pressure of 2.44 atm and an initial volume of 4.01 L. Its pressure changes to 1.93 atm. What is the new volume if temperature and amount are kept constant?

Solution

First, determine what quantities we are given. We are given an initial pressure and an initial volume, so let these values be P₁ and V_1:

P₁ = 2.44 atm and V₁ = 4.01 L

We are given another quantity, final pressure of 1.93 atm, but not a final volume. This final volume is the variable we will solve for.

P₂ = 1.93 atm and V₂ = ? L

Substituting these values into Boyle's law, we get

(2.44 atm)(4.01 L) = (1.93 atm)V₂

To solve for the unknown variable, we isolate it by dividing both sides of the equation by 1.93 atm—both the number and the unit:

\[\frac{(2.44\, atm)(4.01\, L)}{1.93\, atm}=\frac{(1.93\, atm)\, V_{2}}{1.93\, atm}\nonumber \]

Note that, on the left side of the equation, the unit atm is in the numerator and the denominator of the fraction. They cancel algebraically, just as a number would. On the right side, the unit atm and the number 1.93 are in the numerator and the denominator, so the entire quantity cancels:

\[\frac{(2.44\, \cancel{atm})(4.01\, L)}{1.93\, \cancel{atm}}=\frac{(1.93\, \cancel{atm})\, V_{2}}{1.93\, \cancel{atm}}\nonumber \]

What we have left is

\[\frac{(2.44)(4.01\, L)}{1.93}=V_{2}\nonumber \]

Now we simply multiply and divide the numbers together and combine the answer with the \(L\) unit, which is a unit of volume. Doing so, we get \(V_2 = 5.07\, L\)

Does this answer make sense? We know that pressure and volume are inversely related; as one decreases, the other increases. Pressure is decreasing (from 2.44 atm to 1.93 atm), so volume should be increasing to compensate, and it is (from 4.01 L to 5.07 L). So the answer makes sense based on Boyle's law.

Exercise \(\PageIndex{1}\)

If P₁ = 334 torr, V₁ = 37.8 mL, and P₂ = 102 torr, what is V₂?

Answer

124 mL

As mentioned, you can use any units for pressure or volume, but both pressures must be expressed in the same units, and both volumes must be expressed in the same units.

Example \(\PageIndex{2}\)

A sample of gas has an initial pressure of 722 torr and an initial volume of 88.8 mL. Its volume changes to 0.663 L. What is the new pressure?

Solution

We can still use Boyle's law to answer this, but now the two volume quantities have different units. It does not matter which unit we change, as long as we perform the conversion correctly. Let us change the 0.663 L to milliliters:

\[0.663\, L\times \frac{1000\, ml}{1\, L}=663\, ml\nonumber \]

Now that both volume quantities have the same units, we can substitute into Boyle's law:

\[(722\, torr)(88.8\, ml)=P_{2}(663\, ml)\nonumber \]

\[\frac{(722\, torr)(88.8)\, ml}{(663\, ml)}=P_{2}\nonumber \]

The mL units cancel, and we multiply and divide the numbers to get P₂ = 96.7 torr

The volume is increasing, and the pressure is decreasing, which is as expected for Boyle's law.

Exercise \(\PageIndex{2}\)

If V₁ = 456 mL, P₁ = 308 torr, and P₂ = 1.55 atm, what is V₂?

Answer

119 mL

To Your Health: Breathing and Boyle’s Law

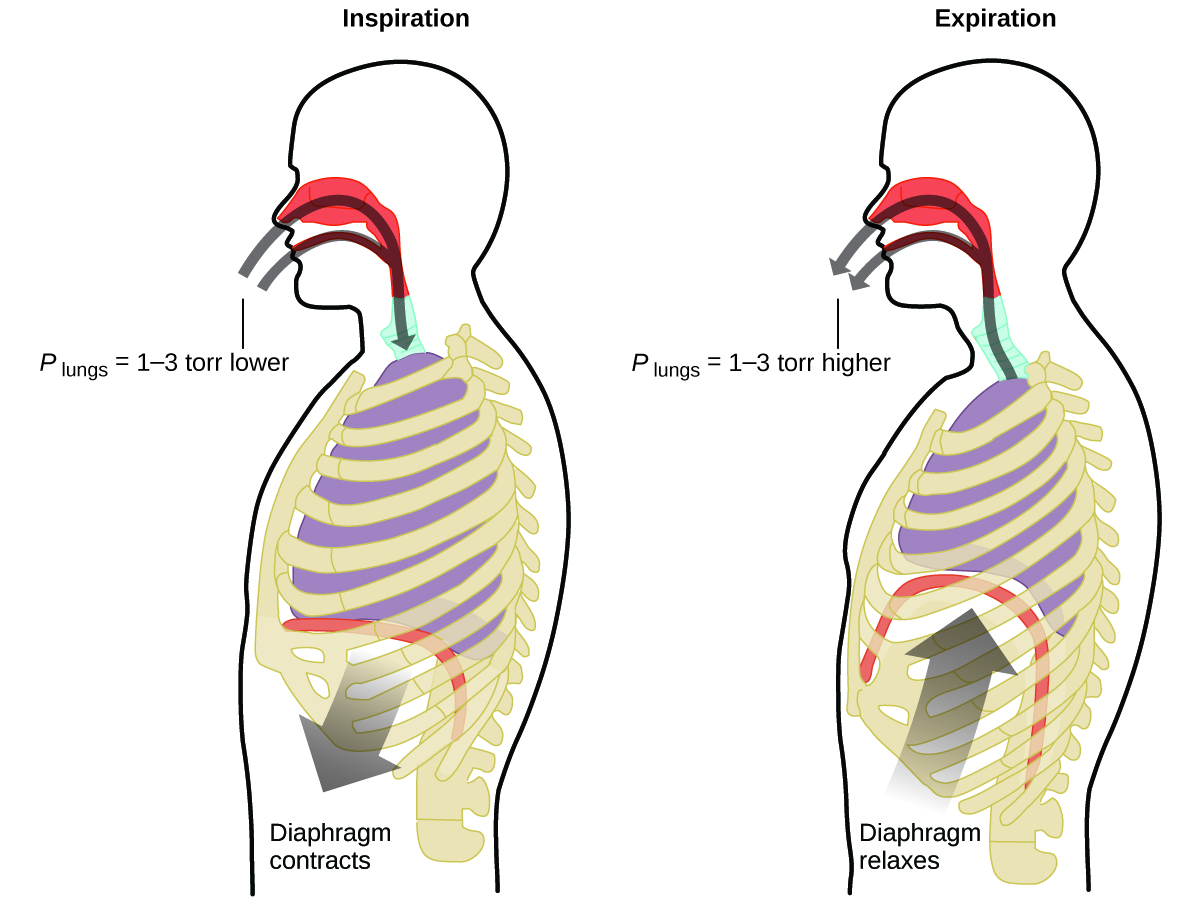
What do you do about 20 times per minute for your whole life, without break, and often without even being aware of it? The answer, of course, is respiration, or breathing. How does it work? It turns out that the gas laws apply here. Your lungs take in gas that your body needs (oxygen) and get rid of waste gas (carbon dioxide). Lungs are made of spongy, stretchy tissue that expands and contracts while you breathe. When you inhale, your diaphragm and intercostal muscles (the muscles between your ribs) contract, expanding your chest cavity and making your lung volume larger. The increase in volume leads to a decrease in pressure (Boyle’s law). This causes air to flow into the lungs (from high pressure to low pressure). When you exhale, the process reverses: Your diaphragm and rib muscles relax, your chest cavity contracts, and your lung volume decreases, causing the pressure to increase (Boyle’s law again), and air flows out of the lungs (from high pressure to low pressure). You then breathe in and out again, and again, repeating this Boyle’s law cycle for the rest of your life (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): Breathing occurs because expanding and contracting lung volume creates small pressure differences between your lungs and your surroundings, causing air to be drawn into and forced out of your lungs.

This figure contains two diagrams of a cross section of the human head and torso. The first diagram on the left is labeled “Inspiration.” It shows curved arrows in gray proceeding through the nasal passages and mouth to the lungs. An arrow points downward from the diaphragm, which is relatively flat, just beneath the lungs. This arrow is labeled “Diaphragm contracts.” At the entrance to the mouth and nasal passages, a label of P subscript lungs equals 1 dash 3 torr lower” is provided. The second, similar diagram, which is labeled “Expiration,” reverses the direction of both arrows. Arrows extend from the lungs out through the nasal passages and mouth. Similarly, an arrow points up to the diaphragm, showing a curved diaphragm and lungs reduced in size from the previous image. This arrow is labeled “Diaphragm relaxes.” At the entrance to the mouth and nasal passages, a label of P subscript lungs equals 1 dash 3 torr higher” is provided.

Summary

• The behavior of gases can be modeled with gas laws.
• Boyle's law relates a gas's pressure and volume at constant temperature and amount.