6.5: Limiting Reagent and Percent Yield
- Page ID
- 86220
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define and determine theoretical yields, actual yields, and percent yields.
- Identify a limiting reagent from a set of reactants.
- Calculate how much product will be produced from the limiting reagent.
- Calculate how much reactant(s) remains when the reaction is complete.
Yield
In all the previous calculations we have performed involving balanced chemical equations, we made two assumptions:
- The reaction goes exactly as written.
- The reaction proceeds completely.
In reality, such things as side reactions occur that make some chemical reactions rather messy. For example, in the actual combustion of some carbon-containing compounds, such as methane, some CO is produced as well as CO2. However, we will continue to ignore side reactions, unless otherwise noted. The second assumption, that the reaction proceeds completely, is more troublesome. Many chemical reactions do not proceed to completion as written, for a variety of reasons. When we calculate an amount of product assuming that all the reactant reacts, we calculate the theoretical yield, an amount that is theoretically produced as calculated using the balanced chemical reaction.
In many cases, however, this is not what really happens. In many cases, less—sometimes, much less—of a product is made during the course of a chemical reaction. The amount that is actually produced in a reaction is called the actual yield. By definition, the actual yield is less than or equal to the theoretical yield. If it is not, then an error has been made.
Both theoretical yields and actual yields are expressed in units of moles or grams. It is also common to see something called a percent yield. The percent yield is a comparison between the actual yield and the theoretical yield and is defined as
\[ \text{percent yield} = \dfrac{\text{actual yield}}{\text{theoretical yield}} \times 100\% \label{yield}\]
It does not matter whether the actual and theoretical yields are expressed in moles or grams, as long as they are expressed in the same units. However, the percent yield always has units of percent. Proper percent yields are between 0% and 100%. In the laboratory, a student will occasionally obtain a yield that appears to be greater than 100%. This usually happens when the product is impure or is wet with a solvent such as water. If this is not the case, then the student must have made an error in weighing either the reactants or the products. The law of conservation of mass applies even to undergraduate chemistry laboratory experiments. A 100% yield means that everything worked perfectly, and the chemist obtained all the product that could have been produced. Anyone who has tried to do something as simple as fill a salt shaker or add oil to a car’s engine without spilling knows the unlikelihood of a 100% yield. At the other extreme, a yield of 0% means that no product was obtained. A percent yield of 80%–90% is usually considered good to excellent; a yield of 50% is only fair. In part because of the problems and costs of waste disposal, industrial production facilities face considerable pressures to optimize the yields of products and make them as close to 100% as possible.
A worker reacts 30.5 g of Zn with nitric acid and evaporates the remaining water to obtain 65.2 g of Zn(NO3)2. What are the theoretical yield, the actual yield, and the percent yield?
\[\ce{Zn(s) + 2HNO_3(aq) → Zn(NO_3)_2(aq) + H_2(g)} \nonumber \]
Solution
A mass-mass calculation can be performed to determine the theoretical yield. We need the molar masses of Zn (65.39 g/mol) and Zn(NO3)2 (189.41 g/mol). In three steps, the mass-mass calculation is:
\[30.5\cancel{g\, Zn}\times \frac{1\, \cancel{mol\, Zn}}{65.39\cancel{g\, Zn}}\times \frac{1\, \cancel{mol\, Zn(NO_{3})_{2}}}{1\cancel{mol\, Zn}}\times \frac{189.41\, g\, Zn(NO_{3})_{2}}{1\cancel{mol\,Zn(NO_{3})_{2}}}=88.3\, g\, Zn(NO_{3})_{2}\nonumber \]
Thus, the theoretical yield is 88.3 g of Zn(NO3)2. The actual yield is the amount that was actually made, which was 65.2 g of Zn(NO3)2. To calculate the percent yield, we take the actual yield and divide it by the theoretical yield and multiply by 100 (Equation \ref{yield}):
\[\frac{65.2\, g\, Zn(NO_{3})_{2}}{88.3\, g\,Zn(NO_{3})_{2}}\times 100\%=73.8\%\nonumber \]
The worker achieved almost three-fourths of the possible yield.
A synthesis produced 2.05 g of NH3 from 16.5 g of N2. What is the theoretical yield and the percent yield?
\[N_2(g) + 3H_2(g) → 2NH_3(g)\nonumber \]
*Technically, this is a reversible reaction (with double arrows), but for this exercise consider it irreversible (single arrow).
Answer
theoretical yield = 20.1 g; percent yield = 10.2%
Many drugs are the product of several steps of chemical synthesis. Each step typically occurs with less than 100% yield, so the overall percent yield might be very small. The general rule is that the overall percent yield is the product of the percent yields of the individual synthesis steps. For a drug synthesis that has many steps, the overall percent yield can be very tiny, which is one factor in the huge cost of some drugs. For example, if a 10-step synthesis has a percent yield of 90% for each step, the overall yield for the entire synthesis is only 35%. Many scientists work every day trying to improve percent yields of the steps in the synthesis to decrease costs, improve profits, and minimize waste.
Even purifications of complex molecules into drug-quality purity are subject to percent yields. Consider the purification of impure albuterol. Albuterol (C13H21NO2; accompanying figure) is an inhaled drug used to treat asthma, bronchitis, and other obstructive pulmonary diseases. It is synthesized from norepinephrine, a naturally occurring hormone and neurotransmitter. Its initial synthesis makes very impure albuterol that is purified in five chemical steps. The details of the steps do not concern us; only the percent yields do:
| impure albuterol → intermediate A | percent yield = 70% |
| intermediate A → intermediate B | percent yield = 100% |
| intermediate B → intermediate C | percent yield = 40% |
| intermediate C → intermediate D | percent yield = 72% |
| intermediate D → purified albuterol | percent yield = 35% |
| overall percent yield = 70% × 100% × 40% × 72% × 35% = 7.5% | |
That is, only about one-fourteenth of the original material was turned into the purified drug. This demonstrates one reason why some drugs are so expensive—a lot of material is lost in making a high-purity pharmaceutical.

Limiting Reagent
In all the examples discussed thus far, the reactants were assumed to be present in stoichiometric quantities. Consequently, none of the reactants was left over at the end of the reaction. This is often desirable, as in the case of a space shuttle, where excess oxygen or hydrogen was not only extra freight to be hauled into orbit but also an explosion hazard. More often, however, reactants are present in mole ratios that are not the same as the ratio of the coefficients in the balanced chemical equation. As a result, one or more of them will not be used up completely but will be left over when the reaction is completed. In this situation, the amount of product that can be obtained is limited by the amount of only one of the reactants. The reactant that restricts the amount of product obtained is called the limiting reactant. The reactant that remains after a reaction has gone to completion is in excess.
Consider a nonchemical example. Assume you have invited some friends for dinner and want to bake brownies for dessert. You find two boxes of brownie mix in your pantry and see that each package requires two eggs. The balanced equation for brownie preparation is thus
\[ 1 \,\text{box mix} + 2 \,\text{eggs} \rightarrow 1 \, \text{batch brownies} \label{3.7.1}\]
If you have a dozen eggs, which ingredient will determine the number of batches of brownies that you can prepare? Because each box of brownie mix requires two eggs and you have two boxes, you need four eggs. Twelve eggs is eight more eggs than you need. Although the ratio of eggs to boxes in is 2:1, the ratio in your possession is 6:1. Hence the eggs are the ingredient (reactant) present in excess, and the brownie mix is the limiting reactant. Even if you had a refrigerator full of eggs, you could make only two batches of brownies.
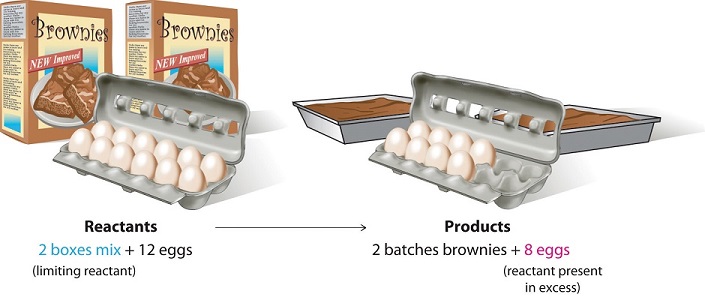
Figure \(\PageIndex{1}\): The Concept of a Limiting Reactant in the Preparation of Brownies
A similar situation exists for many chemical reactions: you usually run out of one reactant before all of the other reactant has reacted. The reactant you run out of is called the limiting reagent; the other reactant or reactants are considered to be in excess. A crucial skill in evaluating the conditions of a chemical process is to determine which reactant is the limiting reagent and which is in excess.
The key to recognizing which reactant is the limiting reagent is based on a mole-mass or mass-mass calculation: whichever reactant gives the lesser amount of product is the limiting reagent. What we need to do is determine an amount of one product (either moles or mass), assuming all of each reactant reacts. Whichever reactant gives the least amount of that particular product is the limiting reagent. It does not matter which product we use, as long as we use the same one each time. It does not matter whether we determine the number of moles or grams of that product; however, we will see shortly that knowing the final mass of product can be useful.
For example, consider this reaction:
\[4As(s) + 3O_2(g) → 2As_2O_3(s)\nonumber \]
Suppose we start a reaction with 50.0 g of As and 50.0 g of O2. Which one is the limiting reagent? We need to perform two mole-mass calculations, each assuming that each reactant reacts completely. Then we compare the amount of the product produced by each and determine which is less.
The calculations are as follows:
\[50.0\cancel{g\, As}\times \frac{1\cancel{mol\, As}}{74.92\cancel{g\, As}}\times \frac{2\, mol\, As_{2}O_{3}}{4\cancel{mol\, As}}=0.334\, mol\, As_{2}O_{3}\nonumber \]
\[50.0\cancel{g\, O_{2}}\times \frac{1\cancel{mol\, O_{2}}}{32.00\cancel{g\, O_{2}}}\times \frac{2\, mol\, As_{2}O_{3}}{3\cancel{mol\, O_{2}}}=1.04\, mol\, As_{2}O_{3}\nonumber \]
Comparing these two answers, it is clear that 0.334 mol of As2O3 is less than 1.04 mol of As2O3, so arsenic is the limiting reagent. If this reaction is performed under these initial conditions, the arsenic will run out before the oxygen runs out. We say that the oxygen is "in excess."
Identifying the limiting reagent, then, is straightforward. However, there are usually two associated questions: (1) what mass of product (or products) is then actually formed? and (2) what mass of what reactant is left over? The first question is straightforward to answer: simply perform a conversion from the number of moles of product formed to its mass, using its molar mass. For As2O3, the molar mass is 197.84 g/mol; knowing that we will form 0.334 mol of As2O3 under the given conditions, we will get
\[0.334\cancel{mol\, As_{2}O_{3}}\times \frac{197.84\, g\, As_{2}}{\cancel{1\, mol\, As_{2}O_{3}}}=66.1\, g\, As_{2}O_{3}\nonumber \]
The second question is somewhat more convoluted to answer. First, we must do a mass-mass calculation relating the limiting reagent (here, As) to the other reagent (O2). Once we determine the mass of O2 that reacted, we subtract that from the original amount to determine the amount left over. According to the mass-mass calculation,
\[50.0\cancel{g\, As}\times \frac{1\cancel{mol\, As}}{74.92\cancel{g\, As}}\times \frac{3\cancel{mol\, O_{2}}}{4\cancel{mol\, As}}\times \frac{32.00\, g\, O_{2}}{\cancel{1\, mol\, O_{2}}}=16.0\, g\, O_{2}\; reacted\nonumber \]
Because we reacted 16.0 g of our original O2, we subtract that from the original amount, 50.0 g, to get the mass of O2 remaining:
50.0 g O2 − 16.0 g O2 reacted = 34.0 g O2 left over
You must remember to perform this final subtraction to determine the amount remaining; a common error is to report the 16.0 g as the amount remaining.
A 5.00 g quantity of Rb is combined with 3.44 g of MgCl2 according to this chemical reaction:
\[2R b(s) + MgCl_2(s) → Mg(s) + 2RbCl(s) \nonumber\nonumber \]
What mass of Mg is formed, and what mass of what reactant is left over?
Solution
Because the question asks what mass of magnesium is formed, we can perform two mass-mass calculations and determine which amount is less.
\[5.00\cancel{g\, Rb}\times \frac{1\cancel{mol\, Rb}}{85.47\cancel{g\, Rb}}\times \frac{1\cancel{mol\, Mg}}{2\cancel{mol\, Rb}}\times \frac{24.31\, g\, Mg}{\cancel{1\, mol\, Mg}}=0.711\, g\, Mg \nonumber \]
\[3.44\cancel{g\, MgCl_{2}}\times \frac{1\cancel{mol\, MgCl_{2}}}{95.21\cancel{g\, MgCl_{2}}}\times \frac{1\cancel{mol\, Mg}}{1\cancel{mol\, MgCl_{2}}}\times \frac{24.31\, g\, Mg}{\cancel{1\, mol\, Mg}}=0.878\, g\, Mg \nonumber \]
The 0.711 g of Mg is the lesser quantity, so the associated reactant—5.00 g of Rb—is the limiting reagent. To determine how much of the other reactant is left, we have to do one more mass-mass calculation to determine what mass of MgCl2 reacted with the 5.00 g of Rb, and then subtract the amount reacted from the original amount.
\[5.00\cancel{g\, Rb}\times \frac{1\cancel{mol\, Rb}}{85.47\cancel{g\, Rb}}\times \frac{1\cancel{mol\, MgCl_{2}}}{2\cancel{mol\, Rb}}\times \frac{95.21\, g\, Mg}{\cancel{1\, mol\, MgCl_{2}}}=2.78\, g\, MgCl_{2}\: \: reacted \nonumber \]
Because we started with 3.44 g of MgCl2, we have
3.44 g MgCl2 − 2.78 g MgCl2 reacted = 0.66 g MgCl2 left
Given the initial amounts listed, what is the limiting reagent, and what is the mass of the leftover reagent?
\[\underbrace{22.7\, g}_{MgO(s)}+\underbrace{17.9\, g}_{H_2S}\rightarrow MgS(s)+H_{2}O(l) \nonumber \]
- Answer
- H2S is the limiting reagent; 1.5 g of MgO are left over.
Summary
Theoretical yield is the calculated yield using the balanced chemical reaction. Actual yield is what is actually obtained in a chemical reaction. Percent yield is a comparison of the actual yield with the theoretical yield.
The limiting reagent is the reactant that produces the least amount of product. Mass-mass calculations can determine how much product is produced and how much of the other reactants remain.

