3.8: Formulas of Ionic Compounds

Learning Objectives

• Write the chemical formula for a simple ionic compound based on the charges of the cations and anions in the compound.

In every ionic compound, the total number of positive charges of the cations equals the total number of negative charges of the anions. Thus, ionic compounds are electrically neutral overall, even though they contain positive and negative ions. We can use this observation to help us write the formula of an ionic compound. The formula of an ionic compound must have a ratio of ions such that the numbers of positive and negative charges are equal.

Ionic Compounds Formed From Monoatomic Ions

Consider an Na atom in the presence of a Cl atom. The two atoms have these Lewis electron dot diagrams and electron configurations:

\[\mathbf{Na\, \cdot }\; \; \; \; \; \; \; \; \; \; \mathbf{\cdot }\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :}\nonumber \]

\[\left [ Ne \right ]3s^{1}\; \; \; \; \left [ Ne \right ]3s^{2}3p^{5}\nonumber \]

For the Na atom to obtain an octet, it must lose an electron; for the Cl atom to obtain an octet, it must gain an electron. An electron transfers from the Na atom to the Cl atom:

\[\mathbf{Na\, \cdot }\curvearrowright \mathbf{\cdot }\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :}\nonumber \]

resulting in two ions—the Na⁺ ion and the Cl⁻ ion:

\[\mathbf{Na\, \cdot }^{+}\; \; \; \; \; \; \; \; \mathbf{:}\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :}^{-}\nonumber \]

\[\left [ Ne \right ]\; \; \; \; \; \left [ Ne \right ]3s^{2}3p^{6}\nonumber \]

Both species now have complete octets, and the electron shells are energetically stable. From basic physics, we know that opposite charges attract. This is what happens to the Na⁺ and Cl⁻ ions:

\[\mathbf{Na\, \cdot }^{+}\; + \; \mathbf{:}\mathbf{\ddot{\underset{.\: .}Cl}}\mathbf{\: :}^{-}\rightarrow Na^{+}Cl^{-}\; \; or\; \; NaCl\nonumber \]

where we have written the final formula (the formula for sodium chloride) as per the convention for ionic compounds, without listing the charges explicitly. As explained previously, the attraction between oppositely charged ions is called an ionic bond.

In electron transfer, the number of electrons lost must equal the number of electrons gained. We saw this in the formation of NaCl. A similar process occurs between Mg atoms and O atoms, except in this case two electrons are transferred:

Magnesium donates two electrons to oxygen to empty its own orbital and fill oxygens, thus creating Mg2+ and O2-.

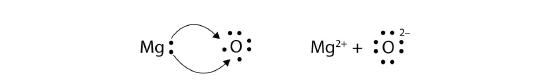
The two ions each have octets as their valence shell, and the two oppositely charged particles attract, making an ionic bond:

\[\mathbf{Mg\,}^{2+}\; + \; \mathbf{:}\mathbf{\ddot{\underset{.\: .}O}}\mathbf{\: :}^{2-}\; \; \; \; \; Mg^{2+}O^{2-}\; or\; MgO\nonumber \]

What about when an Na atom interacts with an O atom? The O atom needs two electrons to complete its valence octet, but the Na atom supplies only one electron:

\[\mathbf{Na\, \cdot }\curvearrowright \mathbf{\cdot }\mathbf{\ddot{\underset{.}O}}\mathbf{\: :}\nonumber \]

The O atom still does not have an octet of electrons. What we need is a second Na atom to donate a second electron to the O atom:

Two sodium atoms donate one electron each to oxygen to empty their orbitals and fill oxygen's, thus creating 2 Na+ and O2-.

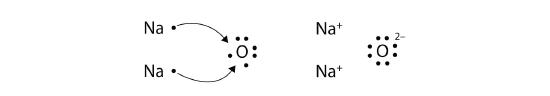
These three ions attract each other to form an overall neutrally charged ionic compound, which we write as Na₂O. The need for the number of electrons lost to be equal to the number of electrons gained explains why ionic compounds have the ratio of cations to anions that they do. This is also required by the law of conservation of matter.

Example \(\PageIndex{1}\)

With arrows, illustrate the transfer of electrons to form calcium chloride from Ca atoms and Cl atoms.

Solution

A Ca atom has two valence electrons, while a Cl atom has seven electrons. A Cl atom needs only one more to complete its octet, while Ca atoms have two electrons to lose. We need two Cl atoms to accept the two electrons from one Ca atom. The transfer process is as follows:

Calcium donates two electrons, one each going to a chlorine. This empties calcium's orbital and fills both of the chlorines'. This creates Ca2+ and two Cl-.

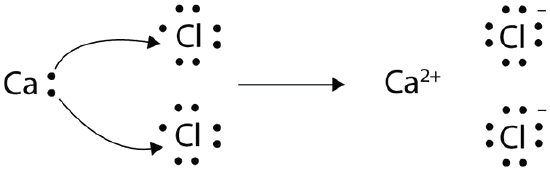
The oppositely charged ions attract one another to make CaCl₂.

Exercise \(\PageIndex{1}\)

With arrows, illustrate the transfer of electrons to form potassium sulfide from K atoms and S atoms.

Answer

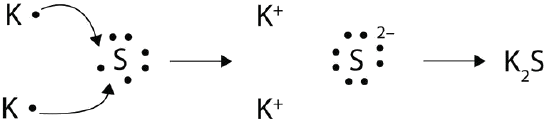
Two potassium atoms donate an electron to sulphur to fill sulphur's orbital and empty their own, thus creating two K+ and one S2-. They ionically bond to form K2S.

For compounds in which the ratio of ions is not as obvious, the subscripts in the formula can be obtained by crossing charges: use the absolute value of the charge on one ion as the subscript for the other ion. This method is shown schematically in Figure 3.3.2.

Figure \(\PageIndex{1}\): Crossing charges. One method for obtaining subscripts in the empirical formula is by crossing charges.

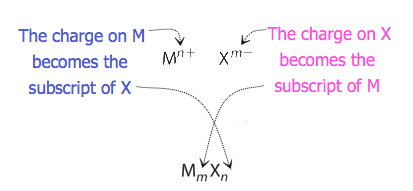
When crossing charges, it is sometimes necessary to reduce the subscripts to their simplest ratio to write the empirical formula. Consider, for example, the compound formed by Pb⁴⁺ and O²⁻. Using the absolute values of the charges on the ions as subscripts gives the formula Pb₂O₄. This simplifies to its correct empirical formula PbO₂. The empirical formula has one Pb⁴⁺ ion and two O²⁻ ions.

Example \(\PageIndex{2}\): Predicting the Formula of an Ionic Compound

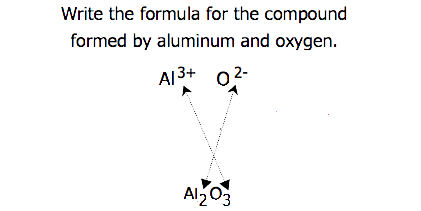
The gemstone sapphire (Figure \(\PageIndex{2}\)) is mostly a compound of aluminum and oxygen that contains aluminum cations, Al³⁺, and oxygen anions, O²⁻. What is the formula of this compound?

Figure \(\PageIndex{2}\): Although pure aluminum oxide is colorless, trace amounts of iron and titanium give blue sapphire its characteristic color. (credit: modification of work by Stanislav Doronenko)

Solution

Because the ionic compound must be electrically neutral, it must have the same number of positive and negative charges. Two aluminum ions, each with a charge of 3+, would give us six positive charges, and three oxide ions, each with a charge of 2−, would give us six negative charges. The formula would be Al₂O₃.

Exercise \(\PageIndex{2}\)

Predict the formula of the ionic compound formed between the sodium cation, Na⁺, and the sulfide anion, S²⁻.

Answer

Na₂S

Ionic Compounds Formed From Polyatomic Ions

Many ionic compounds contain polyatomic ions as the cation, the anion, or both. As with simple ionic compounds, these compounds must also be electrically neutral, so their formulas can be predicted by treating the polyatomic ions as discrete units. We use parentheses in a formula to indicate a group of atoms that behave as a unit. For example, the formula for calcium phosphate, one of the minerals in our bones, is Ca₃(PO₄)₂. This formula indicates that there are three calcium ions (Ca²⁺) for every two phosphate \(\left(\ce{PO4^{3-}}\right)\) groups. The \(\ce{PO4^{3-}}\) groups are discrete units, each consisting of one phosphorus atom and four oxygen atoms, and having an overall charge of 3−. The compound is electrically neutral, and its formula shows a total count of three Ca, two P, and eight O atoms.

Example \(\PageIndex{3}\): Predicting the Formula of a Compound with a Polyatomic Anion

Baking powder contains calcium dihydrogen phosphate, an ionic compound composed of the ions Ca²⁺ and \(\ce{H2PO4-}\). What is the formula of this compound?

Solution

The positive and negative charges must balance, and this ionic compound must be electrically neutral. Thus, we must have two negative charges to balance the 2+ charge of the calcium ion. This requires a ratio of one Ca²⁺ ion to two \(\ce{H2PO4-}\) ions. We designate this by enclosing the formula for the dihydrogen phosphate ion in parentheses and adding a subscript 2. The formula is Ca(H₂PO₄)₂.

Exercise \(\PageIndex{3}\)

Write the chemical formula for an ionic compound composed of each pair of ions.

1. the magnesium ion and the carbonate ion
2. the aluminum ion and the acetate ion

Answer a:

Mg²⁺ and CO₃^2- = MgCO₃

Answer b:

Al³⁺ and C₂H₃O₂^- = Al(C₂H₃O₂)₃

Formula Unit

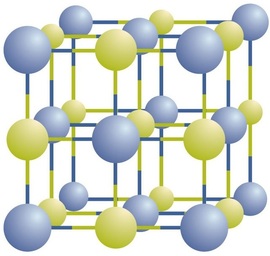
Ionic compounds exist as alternating positive and negative ions in regular, three-dimensional arrays called crystals (Figure \(\PageIndex{3}\)). As you can see, there are no individual \(\ce{NaCl}\) “particles” in the array; instead, there is a continuous lattice of alternating sodium and chloride ions. However, we can use the ratio of sodium ions to chloride ions, expressed in the lowest possible whole numbers or simplest formula, as a way of describing the compound. In the case of sodium chloride, the ratio of sodium ions to chloride ions, expressed in lowest whole numbers, is 1:1, so we use \(\ce{NaCl}\) (one \(\ce{Na}\) symbol and one \(\ce{Cl}\) symbol) to represent the compound. Thus, \(\ce{NaCl}\) is the chemical formula for sodium chloride, which is a concise way of describing the relative number of different ions in the compound. A macroscopic sample is composed of myriads of NaCl pairs; each individual pair called a formula unit. Although it is convenient to think that \(\ce{NaCl}\) crystals are composed of individual \(\ce{NaCl}\) units, Figure \(\PageIndex{3}\) shows that no single ion is exclusively associated with any other single ion. Each ion is surrounded by ions of opposite charge.

Figure \(\PageIndex{3}\): A Sodium Chloride Crystal. A crystal contains a three-dimensional array of alternating positive and negative ions. The precise pattern depends on the compound. A crystal of sodium chloride, shown here, is a collection of alternating sodium and chlorine ions.