3.4: Periodic Properties and Ion Formation
- Page ID
- 86196
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Describe ionization energy and electron affinity and how this relates to ion formation trends.
We have seen that elements often gain or lose enough electrons to achieve the valence electron configuration of the nearest noble gas. Why is this so? In this section, we develop a more quantitative approach to predicting such reactions by examining periodic trends in the energy changes that accompany ion formation.
Ionization Energy
Because atoms do not spontaneously lose electrons, energy is required to remove an electron from an atom to form a cation. Chemists define the ionization energy (\(IE\)) of an element as the amount of energy needed to remove an electron from the gaseous atom \(A\) in its ground state. \(IE\) is therefore the energy required for the reaction:
\[ A(g) \rightarrow A^+(g) + e^- \;\;\ \text{energy required=IE } \label{3.4.1}\]
Because an input of energy is required, the ionization energy is always positive (\(IE > 0\)) for the reaction as written in Equation \(\PageIndex{1}\). Larger values of (\(IE\)) mean that the electron is more tightly bound to the atom and thus, harder to remove. Typical units for ionization energies are kilojoules/mole (kJ/mol) or electron volts (eV):
\[1\; eV / atom = 96.49\; kJ/mol\]
As you move across a row on the periodic table, the ionization energies generally tend to increase. This means that elements on the left side of the periodic table lose electrons more easily (requires less energy to remove an electron) than those on the right side of the periodic table. The trend in ionization energy can be explained by considering the trend in atomic radius (explained in an earlier chapter). As you move from left to right on the periodic table, the atomic size decreases and the electrostatic interactions between the nucleus and valence electrons increases, which increases the energy required to remove electrons, thus the (\(IE\)) increases.
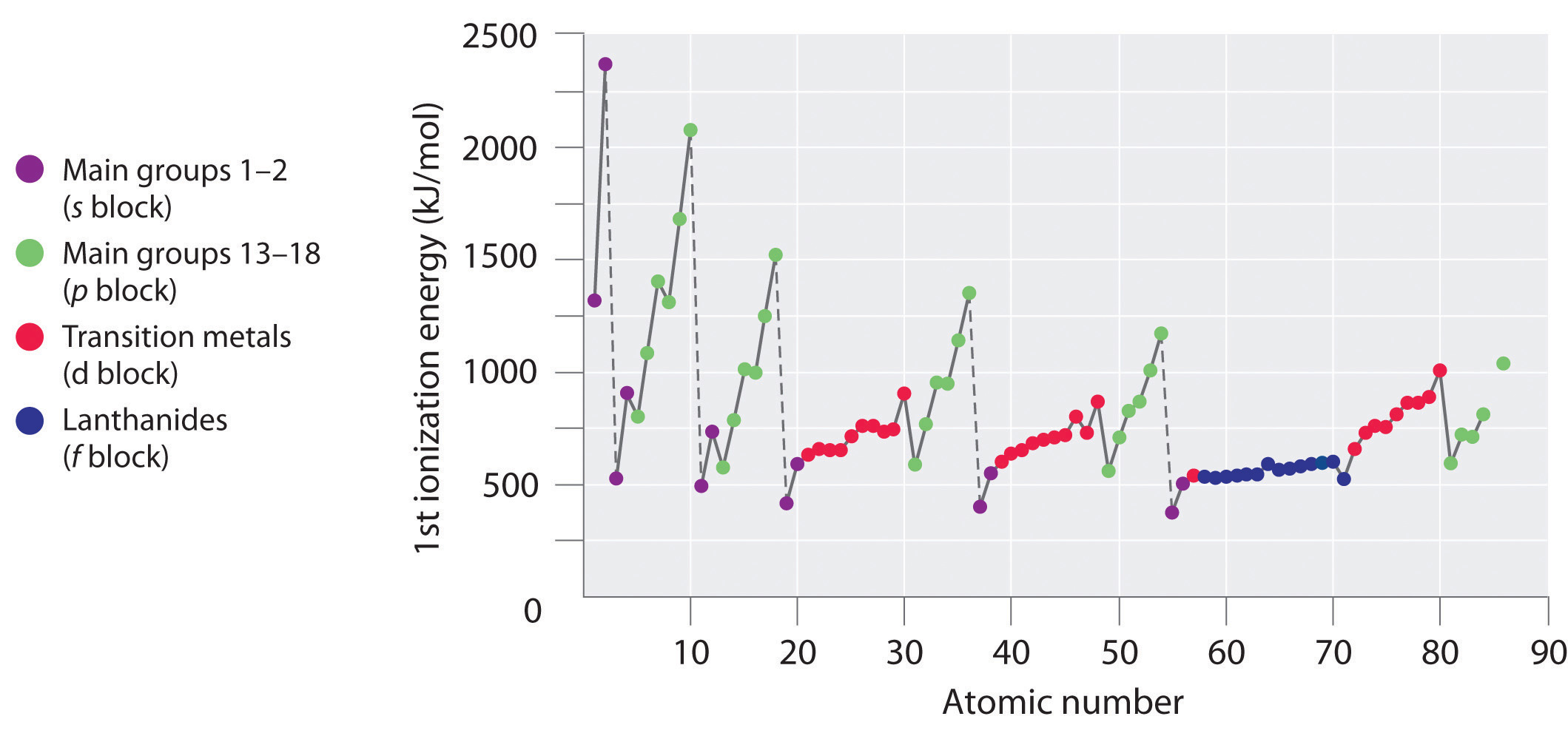
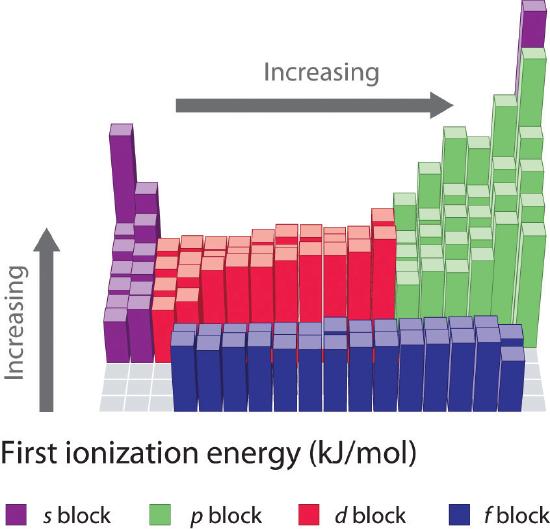
If you look closely at the trends in ionization energy, you will notice that there are some "exceptions" where you see a decrease in energy rather than an increase. In periods 1 and 2, you can see this decrease in (\(IE\)) between groups 2 and 3 and again between groups 5 and 6. These variations in the trend can be further explained by looking closely at the electron configurations of the atoms in question. As you move from magnesium to aluminum, one electron is added to the 3p subshell. This 3p electron is slightly further from the nucleus (higher in energy) and is therefore, more easy to remove compared to the 3s electrons. The decrease between phosphorous and sulfur occurs because the added electron in sulfur is the first to be paired in the p subshell. These two electrons in the same p orbital repel each other, making the sulfur atom slightly less stable than would otherwise be expected, as is true of all the group 16 elements. This electron is easier to remove because it will lead to more stability.
Use their locations in the periodic table to predict which element has the lowest first ionization energy: Ca, K, Mg, Na, Rb, or Sr.
Given: six elements
Asked for: element with lowest first ionization energy
Strategy:
Locate the elements in the periodic table. Based on trends in ionization energies across a row and down a column, identify the element with the lowest first ionization energy.
Solution:
These six elements form a rectangle in the two far-left columns of the periodic table. Because we know that ionization energies increase from left to right in a row and from bottom to top of a column, we can predict that the element at the bottom left of the rectangle will have the lowest first ionization energy: Rb.
Use their locations in the periodic table to predict which element has the highest first ionization energy: As, Bi, Ge, Pb, Sb, or Sn.
- Answer
-
\(\ce{As}\)
Electron Affinity
The electron affinity (\(EA\)) of an element \(A\) is defined as the energy change that occurs when an electron is added to a gaseous atom or ion:
\[ A(g)+e^- \rightarrow A^-(g) \;\;\; \text{energy change=}EA \label{7.5.1}\]
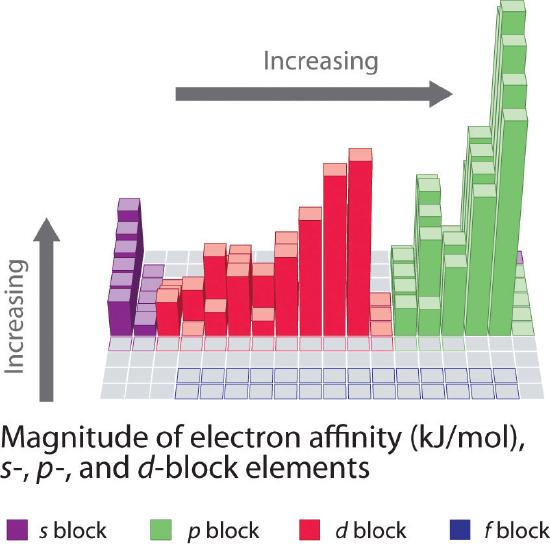
Unlike ionization energies, which are always positive for a neutral atom because energy is required to remove an electron, electron affinities can be negative (energy is released when an electron is added), positive (energy must be added to the system to produce an anion), or zero (the process is energetically neutral). This sign convention is consistent with a negative value corresponded to the energy change for an exothermic process, which is one in which heat is released (Figure \(\PageIndex{2}\)).
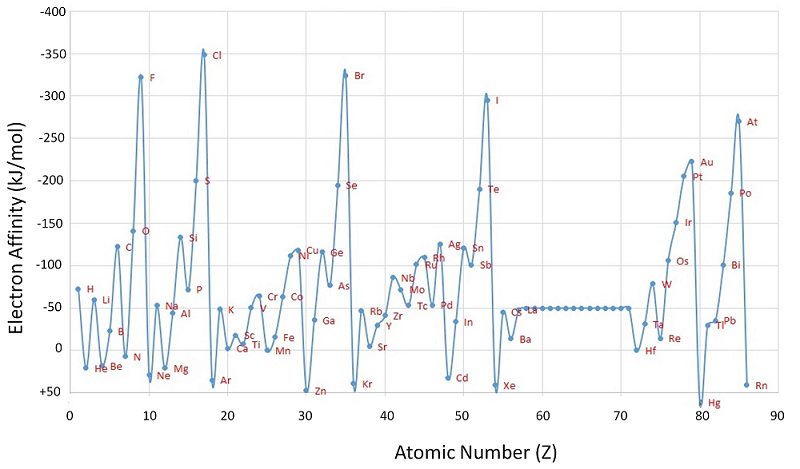
The chlorine atom has the most negative electron affinity of any element, which means that more energy is released when an electron is added to a gaseous chlorine atom than to an atom of any other element:
\[ \ce{ Cl(g) + e^- \rightarrow Cl^- (g)} \;\;\; EA=-346\; kJ/mol \label{7.5.2}\]
In contrast, beryllium does not form a stable anion, so its effective electron affinity is
\[ \ce{ Be(g) + e^- \rightarrow Be^- (g)} \;\;\; EA \ge 0 \label{7.5.3}\]
In general, electron affinities of the main-group elements become less negative as we proceed down a column. This is because as the energy level increases, the extra electrons enter orbitals that are increasingly far from the nucleus, and it is less easy to gain extra electrons forming anions.
Based on their positions in the periodic table, which of Sb, Se, or Te would you predict to have the most negative electron affinity?
Given: three elements
Asked for: element with most negative electron affinity
Strategy:
- Locate the elements in the periodic table. Use the trends in electron affinities going down a column for elements in the same group. Similarly, use the trends in electron affinities from left to right for elements in the same row.
- Place the elements in order, listing the element with the most negative electron affinity first.
Solution:
We know that electron affinities become less negative going down a column (except for the anomalously low electron affinities of the elements of the second row), so we can predict that the electron affinity of Se is more negative than that of Te. We also know that electron affinities become more negative from left to right across a row, and that the group 15 elements tend to have values that are less negative than expected. Because Sb is located to the left of Te and belongs to group 15, we predict that the electron affinity of Te is more negative than that of Sb. The overall order is Se < Te < Sb, so Se has the most negative electron affinity among the three elements.
Based on their positions in the periodic table, which of Rb, Sr, or Xe would you predict to most likely form a gaseous anion?
- Answer
-
Rb

