11.7: Energy from the Nucleus
- Page ID
- 153854
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Explain where nuclear energy comes from.
- Describe the difference between fission and fusion.
- Know key examples of nuclear fission and nuclear fusion.
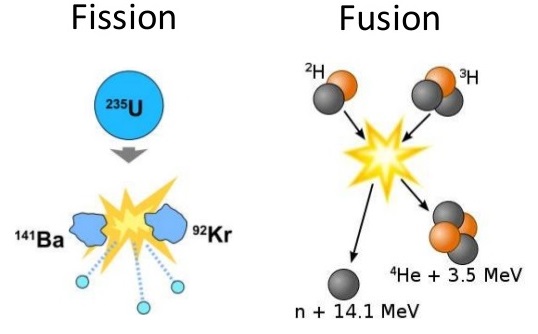
A combination of radiochemistry and radiation chemistry is used to study nuclear reactions such as fission and fusion. Some early evidence for nuclear fission was the formation of a short-lived radioisotope of barium which was isolated from neutron irradiated uranium (139Ba, with a half-life of 83 minutes and 140Ba, with a half-life of 12.8 days, are major fission products of uranium). Nuclear fission is the splitting of an atomic nucleus. In nuclear weapons and reactors, neutrons hit unstable nuclei to form smaller atoms. Nuclear Fusion is the bringing together of two atomic nuclei to form a larger atom. Figure \(\PageIndex{1}\) illustrates the difference between nuclear fission and nuclear fusion.
Einstein and the Equivalence of Mass and Energy
Nuclear changes occur with a simultaneous release of energy. Where does this energy come from? If we could precisely measure the masses of the reactants and products of a nuclear reaction, we would notice that the amount of mass drops slightly in the conversion from reactants to products. Consider the following nuclear equation, in which the molar mass of each species is indicated to four decimal places:
\[_{235.0439}^{235}\textrm{U}\rightarrow _{138.9088}^{139}\textrm{Ba}+_{93.9343}^{94}\textrm{Kr}+_{2\times 1.0087}^{2^{1}}\textrm{n} \nonumber \]
If we compare the mass of the reactant (235.0439) to the masses of the products (sum=234.8605) we notice a mass difference of -0.1834 g or -0.0001834 kg. Where did this mass go?
According to Albert Einstein's theory of relativity, energy (E) and mass (m) are related by the following equation:
\[E = mc^2 \nonumber \]
where c is the speed of light, or \[c=3.00\times 10^{8}\, m/s \nonumber \]
In the course of the chemical reaction for uranium, the mass difference is converted to energy, which is given off by the reaction:
\[E=(-0.0001834\, kg)(3.00\times 10^{8}\, m/s)^{2}=-1.65\times 10^{13}J=-1.65\times 10^{10}kJ \nonumber \]
(For the units to work out, mass must be expressed in units of kilograms.) That is, 16.5 billion kJ of energy is given off every time 1 mol of uranium-235 undergoes this nuclear reaction. This is an extraordinary amount of energy. Compare it to combustion reactions of hydrocarbons, which give off about 650kJ/mol of energy for every CH2 unit in the hydrocarbon-on the order of hundreds of kilojoules per mole. Nuclear reactions give off billions of kilojoules per mole.
If this energy could be properly harvested, it would be a significant source of energy for our society. Nuclear energy involves the controlled harvesting of energy from fission reactions. The reaction can be controlled because the fission of uranium-235 (and a few other isotopes, such as plutonium-239) can be artificially initiated by injecting a neutron into a uranium nucleus. The overall nuclear equation, with energy included as a product, is then as follows:
\[_{}^{235}\textrm{U}\: +\: _{ }^{1}\textrm{n}\rightarrow \: _{ }^{139}\textrm{Ba}\: +\: _{ }^{94}\textrm{Kr}\: +\: 3_{ }^{1}\textrm{n} \nonumber \]
Thus by the careful addition of extra neutrons into a sample of uranium, we can control the fission process and obtain energy that can be used for other purposes. (Artificial or induced radioactivity, in which neutrons are injected into a sample of matter that subsequently cause fission, was first demonstrated in 1934 by Irène Joliot-Curie and Frédéric Joliot, the daughter and son-in-law of Marie Curie.)
Binding Energy
The forces that bind nucleons together in an atomic nucleus are much greater than those that bind an electron to an atom through electrostatic attraction. This is evident by the relative sizes of the atomic nucleus and the atom (\(10^{-15}\) and \(10^{-10}\)m, respectively). The energy required to pry a nucleon from the nucleus is therefore much larger than that required to remove (or ionize) an electron in an atom. In general, all nuclear changes involve large amounts of energy per particle undergoing the reaction. This has numerous practical applications.
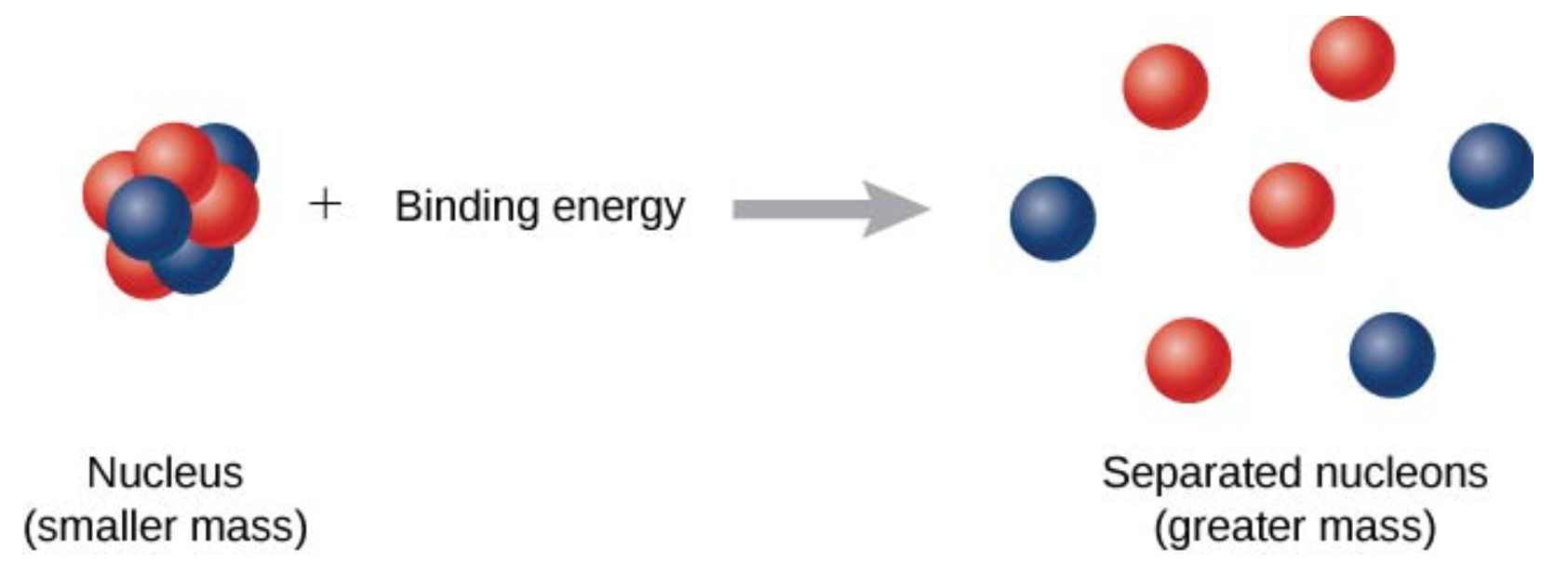
As shown in figure \(\PageIndex{2}\), energy is put into the system to break apart the nucleus. The amount of energy required is called the total binding energy (BE), \(E_b\). The binding energy is equal to the amount of energy released in forming the nucleus, and is therefore given by
\[E_b = (\Delta m)c^2. \label{BE} \]
In nuclear physics, one of the most important experimental quantities is the binding energy per nucleon (BEN), which is defined by
\[BEN = \dfrac{E_b}{A} \label{BEN} \]
This quantity is the average energy required to remove an individual nucleon (proton or neutron) from a nucleus—analogous to the ionization energy of an electron in an atom. If the BEN is relatively large, the nucleus is relatively stable. BEN values are estimated from nuclear scattering experiments.
Figure \(\PageIndex{3}\) shows the relative binding energies for various isotopes. Of these elements, fission requires heavy, unstable nuclei. This means selected atoms would have low binding energies and would have large atomic masses. Nuclei that are larger than Fe-56 may undergo fission. Uranium-238 and uranium-235 both have lower binding energies with heavy masses-.

These two isotopes would be suitable for splitting based on these requirements. Of these two isotopes, only uranium-235 is readily fissionable. This is due to odd neutron count contributing to additional instability. Another fissionable isotope not shown in Figure \(\PageIndex{3}\) is plutonium-239. This is a synthetic isotope produced by transmutation and decay reactions. Like uranium-235, it has low binding energy, high mass, and an odd number of neutrons. U-235 and Pu-239 are used in atomic bombs (fission based) and nuclear reactors.
Positively charged centers of atoms make nuclear fusion extremely difficult. For this reason, smaller atoms are suitable for fusion reactions. In addition, these particular isotopes need to have low binding energies in order to undergo fusion. Atoms that possess these two qualities are H-2 and H-3. For fusion to occur, extreme temperatures are required to fuse these deuterium and tritium together.
As we will see, the BEN-versus-A graph implies that nuclei divided or combined release an enormous amount of energy. This is the basis for a wide range of phenomena, from the production of electricity at a nuclear power plant to sunlight.
Nuclear Fission
In both fission and fusion, large amounts of energy are given off in the form of heat, light, and gamma radiation. Italian physicist, Enrico Fermi, performed the first fission reaction in 1934. He was unaware that he had split a uranium atom into two smaller nuclei. Nuclear fission of heavy elements was discovered on December 17, 1938 by German Otto Hahn and his assistant Fritz Strassmann, and explained theoretically in January 1939 by Lise Meitner (Figure \(\PageIndex{4}\)) and her nephew Otto Robert Frisch. Frisch named the process "fission" by analogy with biological fission of living cells.
Image take from: https://upload.wikimedia.org/wikiped...ner12crop2.J
Since then, fission has been observed in many other isotopes, including most actinide isotopes that have an odd number of neutrons. A typical nuclear fission reaction is shown in Figure \(\PageIndex{5}\).
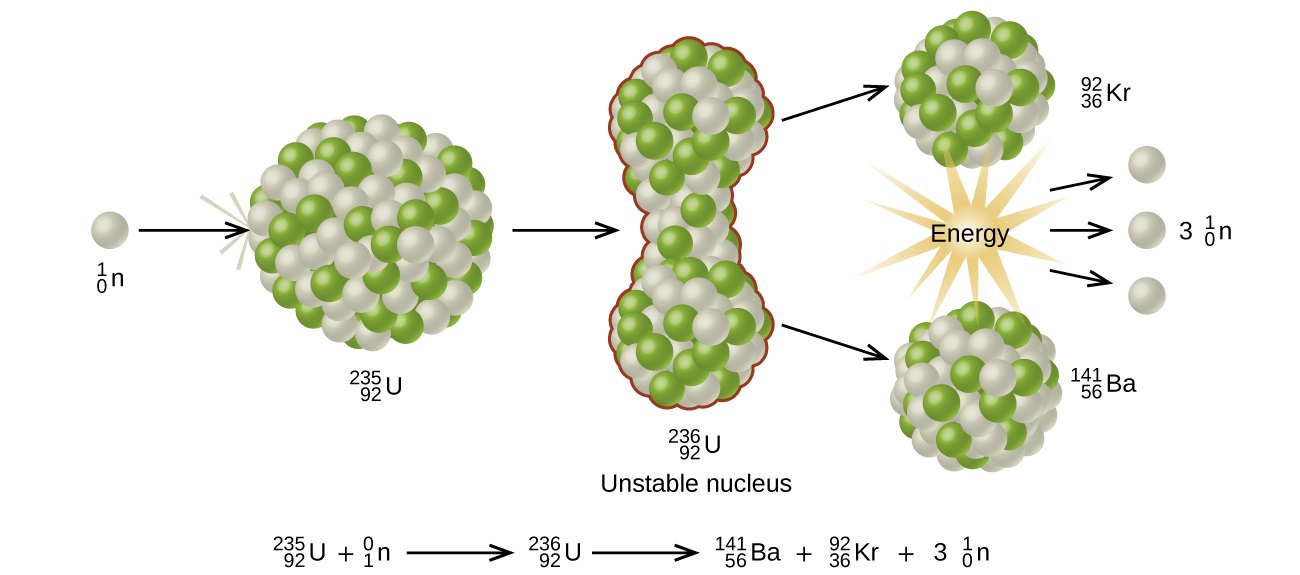
Among the products of Meitner, Hahn, and Strassman’s fission reaction were barium, krypton, lanthanum, and cerium, all of which have nuclei that are more stable than uranium-235. Since then, hundreds of different isotopes have been observed among the products of fissionable substances.
Fission has been used in nuclear weapons and powers all nuclear reactors. Approximately fifty-five countries worldwide possess fission technology in the form of research or energy reactors. Less than ten of these countries have fission weapons.
A tremendous amount of energy is produced by the fission of heavy elements. For instance, when one mole of U-235 undergoes fission, the products weigh about 0.2 grams less than the reactants; this “lost” mass is converted into a very large amount of energy, about 1.8 × 1010 kJ per mole of U-235. Nuclear fission reactions produce incredibly large amounts of energy compared to chemical reactions. The fission of 1 kilogram of uranium-235, for example, produces about 2.5 million times as much energy as is produced by burning 1 kilogram of coal.
Nuclear Chain Reaction
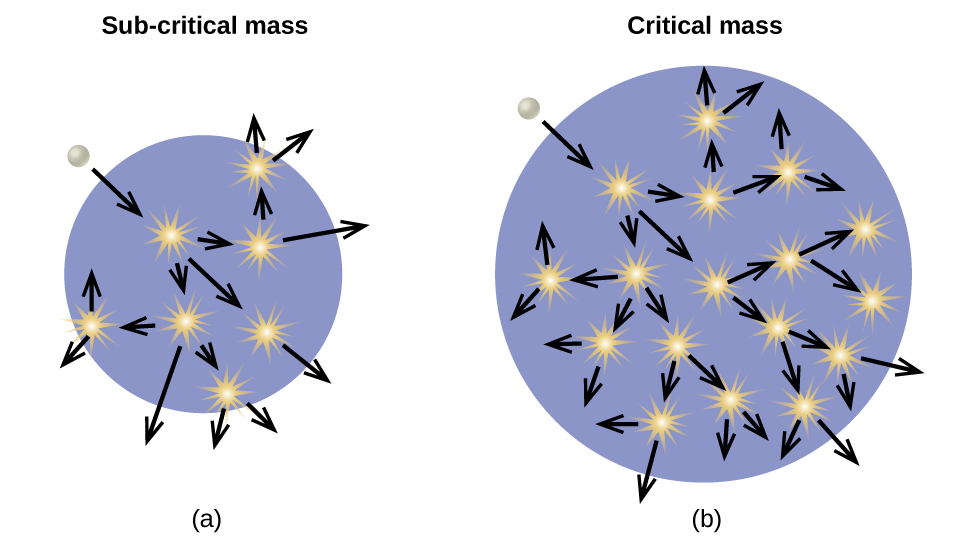
As described earlier, when undergoing fission U-235 produces two “medium-sized” nuclei, and two or three neutrons. These neutrons may then cause the fission of other uranium-235 atoms, which in turn provide more neutrons that can cause fission of even more nuclei, and so on. If this occurs, we have a nuclear chain reaction (Figure \(\PageIndex{6}\)). On the other hand, if too many neutrons escape the bulk material without interacting with a nucleus, then no chain reaction will occur.
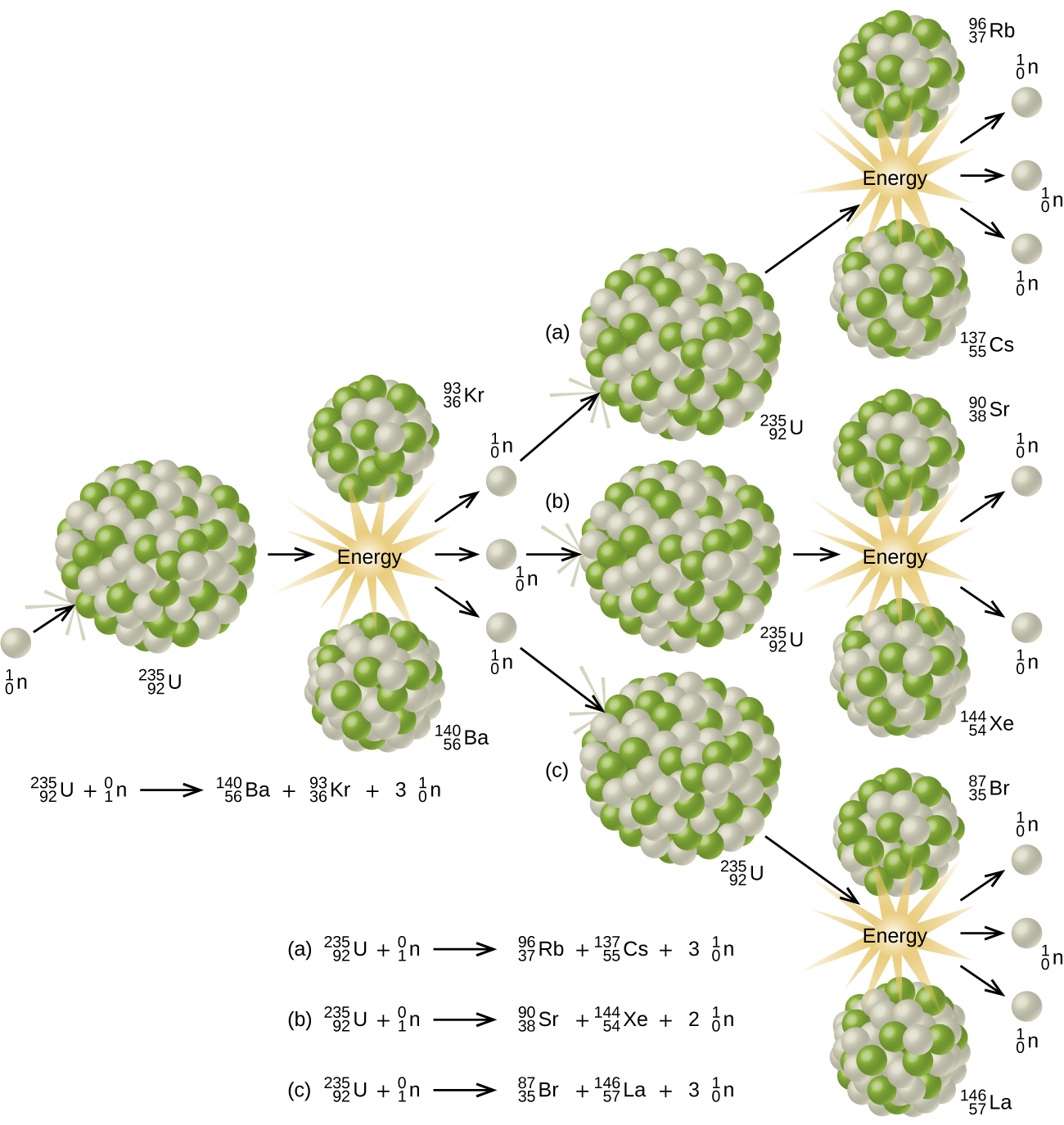
Material that can sustain a nuclear fission chain reaction is said to be fissile or fissionable. (Technically, fissile material can undergo fission with neutrons of any energy, whereas fissionable material requires high-energy neutrons.) Nuclear fission becomes self-sustaining when the number of neutrons produced by fission equals or exceeds the number of neutrons absorbed by splitting nuclei plus the number that escape into the surroundings. The amount of a fissionable material that will support a self-sustaining chain reaction is a critical mass. An amount of fissionable material that cannot sustain a chain reaction is a subcritical mass. An amount of material in which there is an increasing rate of fission is known as a supercritical mass. The critical mass depends on the type of material: its purity, the temperature, the shape of the sample, and how the neutron reactions are controlled (Figure \(\PageIndex{7}\)).
Thermonuclear Reactions
Thermonuclear fusion is a way to achieve nuclear fusion by using extremely high temperatures. There are two forms of thermonuclear fusion: uncontrolled, in which the resulting energy is released in an uncontrolled manner, as it is in thermonuclear weapons ("hydrogen bombs") and in most stars; and controlled, where the fusion reactions take place in an environment allowing some or all of the energy released to be harnessed for constructive purposes. The discussion below is limited to the fusion process that powers the sun and the stars.
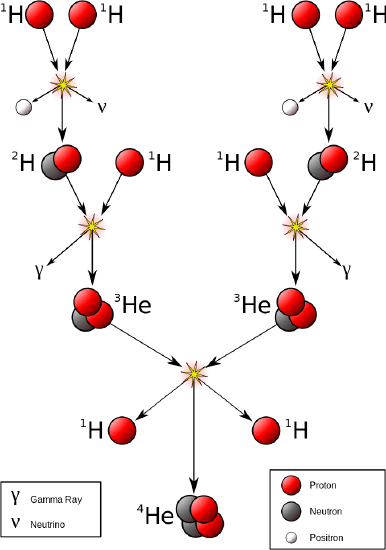
The prime energy producer in the sun is the fusion of hydrogen to form helium, which occurs at a solar-core temperature of 14 million kelvin. The net result is the fusion of four protons into one alpha particle, with the release of two positrons, two neutrinos (which changes two of the protons into neutrons), and energy (Figure \(\PageIndex{8}\)).
This is a net reaction of a more complicated series of events:
\[\ce{4^1_1H ⟶ ^4_2He + 2 ^1_{0}n} \nonumber \]
A helium nucleus has a mass that is 0.7% less than that of four hydrogen nuclei; this lost mass is converted into energy during the fusion. This reaction produces about 3.6 × 1011 kJ of energy per mole of \(\ce{^4_2He}\) produced. This is somewhat larger than the energy produced by the nuclear fission of one mole of U-235 (1.8 × 1010 kJ), and over 3 million times larger than the energy produced by the (chemical) combustion of one mole of octane (5471 kJ).

Summary
- Nuclear energy comes from tiny mass changes in nuclei as radioactive processes occur.
- In fission, large nuclei break apart and release energy; in fusion, small nuclei merge together and release energy.
- The continues process whereby neutrons produced from the initial fission of a large nucleus like U-235 cause further fission of another nucleus.
- In a critical mass, a large enough number of neutrons in the fissile material induce fission to create a chain reaction.
- The most important fusion process in nature is the one that powers the stars. The net result is the fusion of four protons into one alpha particle, with the release of two positrons, two neutrinos (which changes two of the protons into neutrons), and energy
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- TextMap: Beginning Chemistry (Ball et al.)
- Wikipedia

