11.3: Half-Life and Radioisotopic Dating
- Page ID
- 152205
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define half-life.
- Determine the amount of radioactive substance remaining after a given number of half-lives.
- Define a radioactive decay series.
Whether or not a given isotope is radioactive is a characteristic of that particular isotope. Some isotopes are stable indefinitely, while others are radioactive and decay through a characteristic form of emission. As time passes, less and less of the radioactive isotope will be present, and the level of radioactivity decreases. An interesting and useful aspect of radioactive decay is half life. which is the amount of time it takes for one-half of a radioactive isotope to decay. The half-life of a specific radioactive isotope is constant; it is unaffected by conditions and is independent of the initial amount of that isotope.
For example, cobalt-60, an isotope that emits gamma rays used to treat cancer, has a half-life of 5.27 years (Figure \(\PageIndex{1}\)). In a given cobalt-60 source, since half of the \(\ce{^{60}_{27}Co}\) nuclei decay every 5.27 years, both the amount of material and the intensity of the radiation emitted is cut in half every 5.27 years. (Note that for a given substance, the intensity of radiation that it produces is directly proportional to the rate of decay of the substance and the amount of the substance.) This is as expected for a process following first-order kinetics. Thus, a cobalt-60 source that is used for cancer treatment must be replaced regularly to continue to be effective.
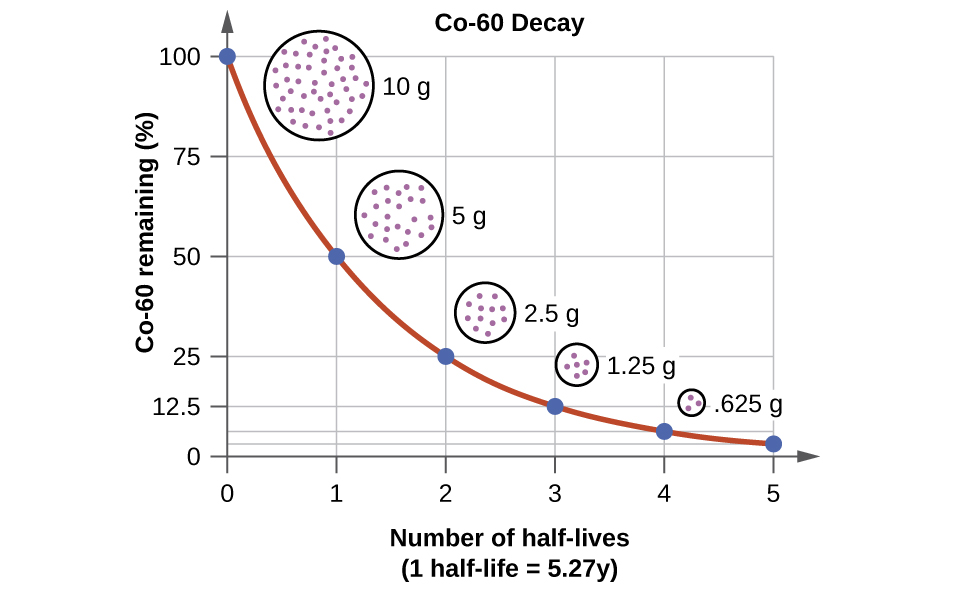
We can determine the amount of a radioactive isotope remaining after a given number half-lives by using the following expression:
\[amount\; \: remaining\: =\: initial\:amount\times \left ( \frac{1}{2} \right )^{n} \nonumber \]
where n is the number of half-lives. This expression works even if the number of half-lives is not a whole number.
The half-life of fluorine-20 is 11.0 s. If a sample initially contains 5.00 g of fluorine-20, how much remains after 44.0 s?
Solution
If we compare the time that has passed to the isotope's half-life, we note that 44.0 s is exactly 4 half-lives, so using the previous expression, n = 4. Substituting and solving results in the following:
\[amount\; \: remaining\: =\: 5.00g\times \left ( \frac{1}{2} \right )^{4}\\ amount\; \: remaining\: =\: 5.00g\times \left ( \frac{1}{16} \right )\\ amount\; \: remaining\: =\: 0.313g \nonumber \]
Less than one-third of a gram of fluorine-20 remains.
The half-life of titanium-44 is 60.0 y. A sample of titanium contains 0.600 g of titanium-44. How much remains after 240.0 y?
- Answer
-
0.0375 g
If there are 60 grams of \(\ce{Np}\)-240 present, how much \(\ce{Np}\)-240 will remain after 4 hours? (\(\ce{Np}\)-240 has a half-life of 1 hour)
Solution
\(\ce{Np}\)-240 with a half life of only 1 hour.

After 4 hours, only \(3.75 \: \text{g}\) of our original \(60 \: \text{g}\) sample would remain the radioactive isotope \(\ce{Np}\)-240.
A sample of \(\ce{Ac}\)-225 originally contained 80 grams and after 50 days only 2.55 grams of the original \(\ce{Ac}\)-225 remain. What is the half life of \(\ce{Ac}\)-225?
Answer
10 days.
The half-lives of many radioactive isotopes have been determined and they have been found to range from extremely long half-lives of 10 billion years to extremely short half-lives of fractions of a second. For example: the half-life of \(\ce{^{209}_{83}Bi}\) is 1.9 × 1019 years; \(\ce{^{239}_{94}Ra}\) is 24,000 years; \(\ce{^{222}_{86}Rn}\) is 3.82 days; and element-111 (Rg for roentgenium) is 1.5 × 10–3 seconds. The table below illustrates half-lives for several selected elements.
| Element | Mass Number (A) | Half-life | Element | Mass Number (A) | Half Life |
|---|---|---|---|---|---|
| Uranium | 238 | 4.5 Billion years | Californium | 251 | 800 years |
| Neptunium | 240 | 1 hour | Nobelium | 254 | 3 seconds |
| Plutonium | 243 | 5 hours | Carbon | 14 | 5730 years |
| Americium | 245 | 25 minutes | Carbon | 16 | 740 milliseconds |
Uranium Decay Series
The naturally occurring radioactive isotopes of the heaviest elements fall into chains of successive disintegrations, or decays, and all the species in one chain constitute a radioactive family, or radioactive decay series. Three of these series include most of the naturally radioactive elements of the periodic table. They are the uranium series, the actinide series, and the thorium series. (Figure \(\PageIndex{2}\)). In all three series, the end-product is a stable isotope of lead.

Radioactive Dating
Radioactive dating is a process by which the approximate age of an object is determined through the use of certain radioactive nuclides. For example, carbon-14 has a half-life of 5,730 years and is used to measure the age of organic material. The ratio of carbon-14 to carbon-12 in living things remains constant while the organism is alive because fresh carbon-14 is entering the organism whenever it consumes nutrients. When the organism dies, this consumption stops, and no new carbon-14 is added to the organism. As time goes by, the ratio of carbon-14 to carbon-12 in the organism gradually declines, because carbon-14 radioactively decays while carbon-12 is stable. Analysis of this ratio allows archaeologists to estimate the age of organisms that were alive many thousands of years ago. For example, with the half-life of \(\ce{^{14}_6C}\) being 5730 years, if the \(\ce{^{14}_6C : ^{12}_6C}\) ratio in a wooden object found in an archaeological dig is half what it is in a living tree, this indicates that the wooden object is 5730 years old.
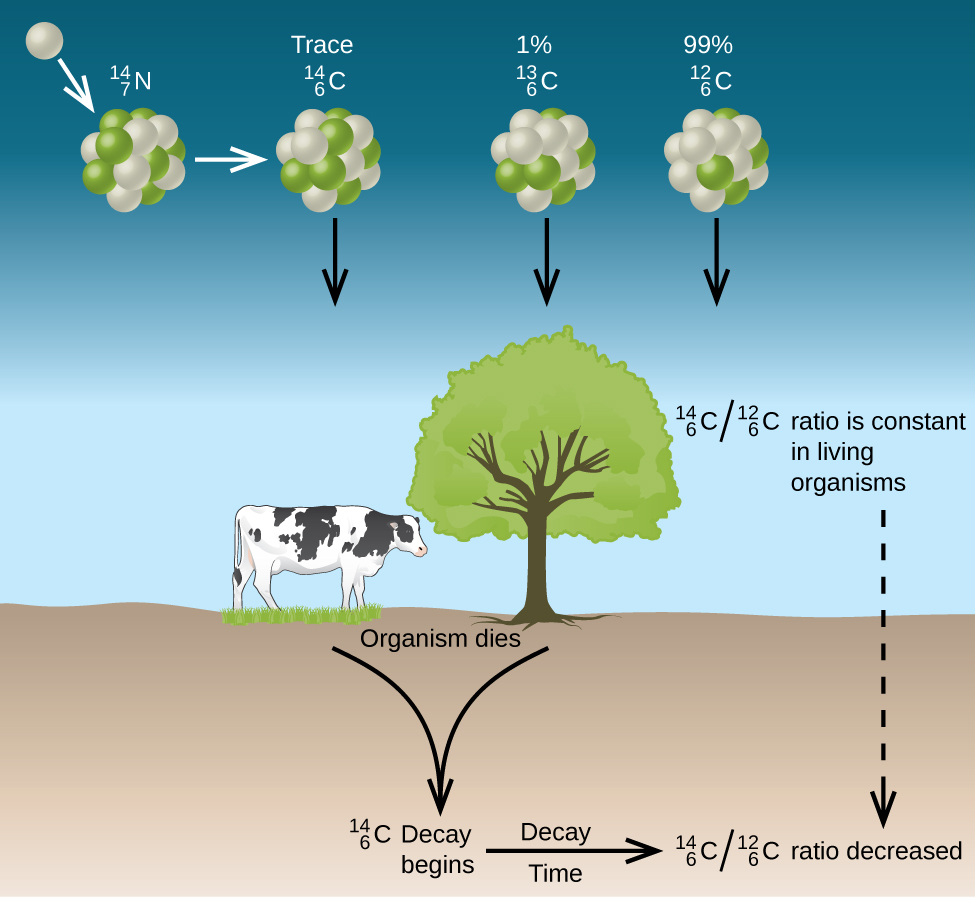
C-14 dating does have limitations. For example, a sample can be C-14 dating if it is approximately 100 to 50,000 years old. Before or after this range, there is too little of the isotope to be detected. Substances must have obtained C-14 from the atmosphere. For this reason, aquatic samples cannot be effectively C-14 dated. Lastly, accuracy of C-14 dating has been affected by atmosphere nuclear weapons testing. Fission bombs ignite to produce more C-14 artificially. Samples tested during and after this period must be checked against another method of dating (isotopic or tree rings).
To calculate the age of a substance using isotopic dating, use the equation below:
\[ \text{how old (time)} = n \times t_{1/2} \nonumber \]
where \(n\) is the number of half-lives and \(t_{1/2}\) is the half-life (in time).
How long will it take for 18.0 grams of Ra-226 to decay to leave a total of 2.25 grams? Ra-226 has a half-life of 1600 years.
Solution
18.0g ⇒ 9.0g ⇒ 4.5g ⇒ 2.25g, this is three half-lives
\[ \text{how old (time)} = 3 \times 1600\, years \nonumber \]
This decay process takes 4800 years to occur.
A National Historic Chemical Landmark -American Chemical Society
Dedic ated at the University of Chicago on October 10, 2016.
ated at the University of Chicago on October 10, 2016.
In 1946, Willard Libby proposed an innovative method for dating organic materials by measuring their content of carbon-14, a newly discovered radioactive isotope of carbon. Known as radiocarbon dating, this method provides objective age estimates for carbon-based objects that originated from living organisms. The “radiocarbon revolution” made possible by Libby’s discovery greatly benefited the fields of archaeology and geology by allowing practitioners to develop more precise historical chronologies across geography and cultures.
Willard F. Libby (right), the physical chemist who conceived of radiocarbon dating, with graduate student Ernest Anderson.
University of Chicago Photographic Archive, apf1-03868, Special Collections Research Center, University of Chicago Library.
Go to Link below for more details
www.acs.org/content/acs/en/education/whatischemistry/landmarks/radiocarbon-dating.html
Radioactive Dating Using Nuclides Other than Carbon-14
Radioactive dating can also use other radioactive nuclides with longer half-lives to date older events. An ingenious application of half-life studies established a new science of determining ages of materials by half-life calculations. For geological dating, the decay of \(\ce{U}\)-238 can be used. The half-life of \(\ce{U}\)-238 is \(4.5 \times 10^9\) years. The end product of the decay of \(\ce{U}\)-238 is \(\ce{Pb}\)-206. After one half-life, a 1.00 gram sample of uranium will have decayed to 0.50 grams of \(\ce{U}\)-238 and 0.43 grams of \(\ce{Pb}\)-206. By comparing the amount of \(\ce{U}\)-238 to the amount of \(\ce{Pb}\)-206 in a sample of uranium mineral, the age of the mineral can be estimated. Present day estimates for the age of the Earth's crust from this method is at 4 billion years. This radioactivity approach can be used to detecting fake wine vintages too.
Isotopes with shorter half-lives are used to date more recent samples. For example, tritium (t1/2 =12.3 years) can date samples within an age range of 1-100 years. Chemists and geologists use tritium dating to determine the age of water (ocean and fresh). In addition, tritium dating can be useful in determining the age of wines and brandies.
K-40 decays by positron emission and electron capture to form Ar-40 with a half-life of 1.25 billion years. If a rock sample is crushed and the amount of Ar-40 gas that escapes is measured, determination of the Ar-40:K-40 ratio yields the age of the rock. Other methods, such as rubidium-strontium dating (Rb-87 decays into Sr-87 with a half-life of 48.8 billion years), operate on the same principle. To estimate the lower limit for the earth’s age, scientists determine the age of various rocks and minerals, making the assumption that the earth is older than the oldest rocks and minerals in its crust. As of 2014, the oldest known rocks on earth are the Jack Hills zircons from Australia, found by uranium-lead dating to be almost 4.4 billion years old.
Summary
- Natural radioactive processes are characterized by a half-life, the time it takes for half of the material to decay radioactively.
- The amount of material left over after a certain number of half-lives can be determined using the following expression:
\[amount\; \: remaining\: =\: initial\:amount\times \left ( \frac{1}{2} \right )^{n} \nonumber \]
where n is the number of half-lives.
- \(\ce{C}\)-14 dating procedures have been used to determine the age of organic artifacts. Its half-life is approximately 5700 years.
Contributors and Attributions
- TextMap: Beginning Chemistry (Ball et al.)
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).
- American Chemical Society-Chemical Landmarks

