11.2: Nuclear Equations
- Page ID
- 152204
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify common particles and energies involved in nuclear reactions.
- Write and balance nuclear equations.
Changes of nuclei that result in changes in their atomic numbers, mass numbers, or energy states are nuclear reactions. To describe a nuclear reaction, we use an equation that identifies the nuclides involved in the reaction, their mass numbers and atomic numbers, and the other particles involved in the reaction.
Types of Particles in Nuclear Reactions
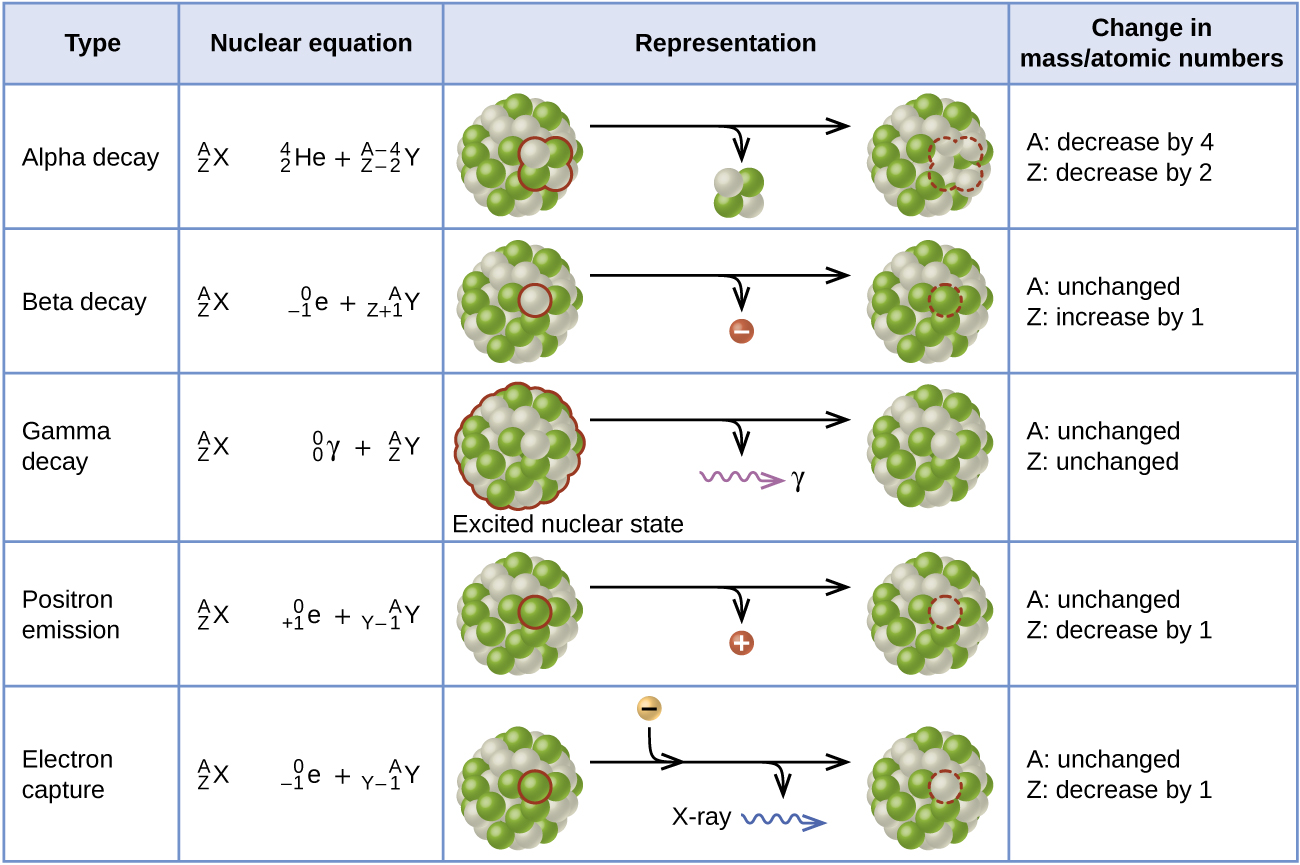
Many entities can be involved in nuclear reactions. The most common are protons, neutrons, alpha particles, beta particles, positrons, and gamma rays, as shown in Table \(\PageIndex{1}\).
Table \(\PageIndex{1}\) A Summary of the Names, Symbols, Representations, and Descriptions of the Most Common Particles in Nuclear Reactions.

Balancing Nuclear Reactions
A balanced chemical reaction equation reflects the fact that during a chemical reaction, bonds break and form, and atoms are rearranged, but the total numbers of atoms of each element are conserved and do not change. A balanced nuclear reaction equation indicates that there is a rearrangement during a nuclear reaction, but of subatomic particles rather than atoms. Nuclear reactions also follow conservation laws, and they are balanced in two ways:
- The sum of the mass numbers of the reactants equals the sum of the mass numbers of the products.
- The sum of the charges of the reactants equals the sum of the charges of the products.
If the atomic number and the mass number of all but one of the particles in a nuclear reaction are known, we can identify the particle by balancing the reaction. For instance, we could determine that \(\ce{^{17}_8O}\) is a product of the nuclear reaction of \(\ce{^{14}_7N}\) and \(\ce{^4_2He}\) if we knew that a proton, \(\ce{^1_1H}\), was one of the two products. Example \(\PageIndex{1}\) shows how we can identify a nuclide by balancing the nuclear reaction.
Nuclear Decay Processes
Radioactive decay involves the emission of a particle and/or energy as one atom changes into another. In most instances, the atom changes its identity to become a new element. There are four different types of emissions that occur.
Alpha Emission
Alpha \(\left( \alpha \right)\) decay involves the release of helium ions from the nucleus of an atom. This ion consists of two protons and two neutrons and has a \(2+\) charge. Release of an \(\alpha\)-particle produces a new atom that has an atomic number two less than the original atom and an atomic weight that is four less. A typical alpha decay reaction is the conversion of uranium-238 to thorium:
\[\ce{^{238}_{92}U} \rightarrow \ce{^{234}_{90}Th} + \ce{^4_2 \alpha}^+ \nonumber \]
We see a decrease of two in the atomic number (uranium to thorium) and a decrease of four in the atomic weight (238 to 234). Usually the emission is not written with atomic number and weight indicated since it is a common particle whose properties should be memorized. Quite often the alpha emission is accompanied by gamma \(\left( \gamma \right)\) radiation, a form of energy release. Many of the largest elements in the periodic table are alpha-emitters.
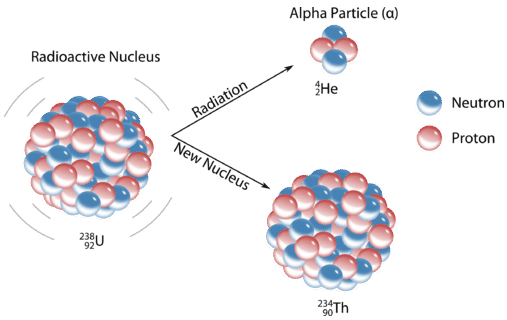
Chemists often use the names parent isotope and daughter isotope to represent the original atom and the product other than the alpha particle. In the previous example, \[_{92}^{238}\textrm{U} \nonumber \] is the parent isotope, and \[_{90}^{234}\textrm{Th} \nonumber \] is the daughter isotope. When one element changes into another in this manner, it undergoes radioactive decay.
Write the nuclear equation that represents the radioactive decay of radon-222 by alpha particle emission and identify the daughter isotope.
Solution
Radon has an atomic number of 86, so the parent isotope is represented as \[_{86}^{222}\textrm{Rn} \nonumber \]
We represent the alpha particle as
\[_{2}^{4}\textrm{He} \nonumber \]
Use subtraction (222 − 4 = 218 and 86 − 2 = 84) to identify the daughter isotope as polonium:
\[_{86}^{222}\textrm{Rn}\rightarrow \; _{2}^{4}\textrm{He}+\: _{84}^{218}\textrm{Th} \nonumber \]
Write the nuclear equation that represents radioactive decay of polonium-208 by alpha particle emission and identify the daughter isotope.
- Answer
-
\[_{80}^{208}\textrm{Po}\rightarrow \; _{2}^{4}\textrm{He}+\: _{82}^{204}\textrm{Pb} \nonumber \]
\[_{82}^{204}\textrm{Pb} \nonumber \]
Beta Emission
Beta \(\left( \beta \right)\) decay is a more complicated process. Unlike the \(\alpha\)-emission, which simply expels a particle, the \(\beta\)-emission involves the transformation of a neutron in the nucleus to a proton and an electron. The electron is then ejected from the nucleus. In the process,the atomic number increases by one while the atomic weight stays the same. As is the case with \(\alpha\)-emissions, \(\beta\)-emissions are often accompanied by \(\gamma\)-radiation.
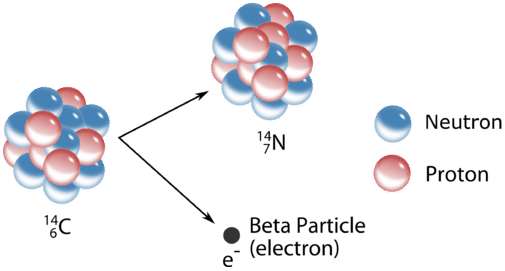
A typical beta decay process involves carbon-14, often used in radioactive dating techniques. The reaction forms nitrogen-14 and an electron:
\[\ce{^{14}_6C} \rightarrow \ce{^{14}_7N} + \ce{^0_{-1}e} \nonumber \]
Again, the beta emission is usually simply indicated by the Greek letter \(\beta\); memorization of the process is necessary in order to follow nuclear calculations in which the Greek letter \(\beta\) appears without further notation.
Write the nuclear equation that represents the radioactive decay of boron-12 by beta particle emission and identify the daughter isotope. A gamma ray is emitted simultaneously with the beta particle.
Solution
The parent isotope is \[