6.6: The Ideal Gas Law and Some Applications
- Page ID
- 64042
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Learn the ideal gas law.
- Apply the ideal gas law to any set of conditions of a gas.
- Apply the ideal gas law to molar volumes, density, and stoichiometry problems.
So far, the gas laws we have considered have all required that the gas change its conditions; then we predict a resulting change in one of its properties. Are there any gas laws that relate the physical properties of a gas at any given time? Consider a further extension of the combined gas law to include n. By analogy to Avogadro's law, n is positioned in the denominator of the fraction, opposite the volume. So,
\[\frac{PV}{nT}=constant\nonumber \]
Because pressure, volume, temperature, and amount are the only four independent physical properties of a gas, the constant in the above equation is truly a constant. Indeed, because we do not need to specify the identity of a gas to apply the gas laws, this constant is the same for all gases. We define this constant with the symbol R, so the previous equation is written as
\[\dfrac{PV}{nT}=R\nonumber \]
which is usually rearranged as
\[PV = nRT\nonumber \]
This equation is called the ideal gas law. It relates the four independent properties of a gas at any time. The constant \(R\) is called the ideal gas law constant. Its value depends on the units used to express pressure and volume.
| Numerical Value | Units |
|---|---|
| 0.08205 | \(\dfrac{L.atm}{mol.K}\) |
| 62.36 | \(\dfrac{L.torr}{mol.K}=\dfrac{L.mmHg}{mol.K}\) |
| 8.314 | \(\dfrac{J}{mol.K}\) |
The ideal gas law is used like any other gas law, with attention paid to the unit and expression of the temperature in kelvin. However, the ideal gas law does not require a change in the conditions of a gas sample. The ideal gas law implies that if you know any three of the physical properties of a gas, you can calculate the fourth property.
A 4.22 mol sample of \(\ce{Ar}\) has a pressure of 1.21 atm and a temperature of 34°C. What is its volume?
Solution
The first step is to convert temperature to kelvins:
\[34 + 273 = 307\, \ce{K} \nonumber\]
Now we can substitute the conditions into the ideal gas law:
\[(1.21atm)(V)=(4.22\, mol)\left(0.08205\dfrac{L.atm}{mol.K}\right)(307\, K)\nonumber \]
The atm unit is in the numerator of both sides, so it cancels. On the right side of the equation, the mol and K units appear in the numerator and the denominator, so they cancel as well. The only unit remaining is L, which is the unit of volume that we are looking for. We isolate the volume variable by dividing both sides of the equation by 1.21:
\[V=\dfrac{(4.22)(0.08205)(307)}{1.21}L\nonumber \]
Then solving for volume, we get V = 87.9 L
A 0.0997 mol sample of \(\ce{O2}\) has a pressure of 0.692 atm and a temperature of 333 K. What is its volume?
- Answer
-
3.94 L
At a given temperature, 0.00332 g of Hg in the gas phase has a pressure of 0.00120 mmHg and a volume of 435 L. What is its temperature?
Solution
We are not given the number of moles of Hg directly, but we are given a mass. We can use the molar mass of Hg to convert to the number of moles.
\[0.00332\cancel{g\, Hg}\times \frac{1\, mol\, Hg}{200.59\cancel{g\, \, Hg}}=0.0000165\, mol=1.65\times 10^{-5}mol\nonumber \]
Pressure is given in units of millimeters of mercury. We can either convert this to atmospheres or use the value of the ideal gas constant that includes the mmHg unit. We will take the second option. Substituting into the ideal gas law,
\[(0.00332\, mm\, Hg)(435\, L)=(1.65\times 10^{-5}mol)(62.36\frac{L.mmHg}{mol.K})T\nonumber \]
The mmHg, L, and mol units cancel, leaving the K unit, the unit of temperature. Isolating T on one side, we get
\[T=\frac{(0.00332)(435)}{(1.65\times 10^{-5})(62.36)}K\nonumber \]
Then solving for K, we get T = 1,404 K.
For a 0.00554 mol sample of H2, P = 23.44 torr and T = 557 K. What is its volume?
- Answer
-
8.21 L
The ideal gas law can also be used in stoichiometry problems.
What volume of \(\ce{H2}\) is produced at 299 K and 1.07 atm when 55.8 g of \(\ce{Zn}\) metal react with excess \(\ce{HCl}\)?
\[\ce{Zn(s) + 2HCl(aq) -> ZnCl2(aq) + H2(g)}\nonumber \]
Solution
Here we have a stoichiometry problem where we need to find the number of moles of H2 produced. Then we can use the ideal gas law, with the given temperature and pressure, to determine the volume of gas produced. First, the number of moles of H2 is calculated:
\[55.8\cancel{g\, Zn}\times \frac{1\cancel{mol\, Zn}}{65.41\cancel{g\, Zn}}\times \dfrac{1\, mol\, H_{2}}{1\cancel{mol\, Zn}}=0.853\, H_{2}\nonumber \]
Now that we know the number of moles of gas, we can use the ideal gas law to determine the volume, given the other conditions:
\[(1.07atm)V=(0.853\, mol)\left(0.08205\dfrac{L.atm}{mol.K}\right)(299\, K)\nonumber \]
All the units cancel except for L, for volume, which means V = 19.6 L
What pressure of \(\ce{HCl}\) is generated if 3.44 g of \(\ce{Cl2}\) are reacted in 4.55 L at 455 K?
\[\ce{H2(g) + Cl2(g) → 2HCl(g)}\nonumber \]
- Answer
-
0.796 atm
It should be obvious by now that some physical properties of gases depend strongly on the conditions. What we need is a set of standard conditions so that properties of gases can be properly compared to each other. Standard Temperature and Pressure (STP) is defined as exactly 100 kPa of pressure (0.986 atm) and 273 K (0°C). For simplicity, we will use 1 atm as standard pressure. Defining STP allows us to more directly compare the properties of gases that differ from one another.
One property shared among gases is a molar volume. The molar volume is the volume of 1 mol of a gas. At STP, the molar volume of a gas can be easily determined by using the ideal gas law:
\[(1\, atm)V=(1\, mol) \left(0.08205\dfrac{L.atm}{mol.K}\right)(273\, K)\nonumber \]
All the units cancel except for L, the unit of volume. So V = 22.4 L
Note that we have not specified the identity of the gas; we have specified only that the pressure is 1 atm and the temperature is 273 K. This makes for a very useful approximation: any gas at STP has a volume of 22.4 L per mole of gas; that is, the molar volume at STP is 22.4 L/mol (Figure \(\PageIndex{1}\)). This molar volume makes a useful conversion factor in stoichiometry problems if the conditions are at STP. If the conditions are not at STP, a molar volume of 22.4 L/mol is not applicable. However, if the conditions are at STP, the combined gas law can be used to calculate what the volume of the gas would be if at STP; then the 22.4 L/mol molar volume can be used.
How many moles of \(\ce{Ar}\) are present in 38.7 L at STP?
Solution
We can use the molar volume, 22.4 L/mol, as a conversion factor, but we need to reverse the fraction so that the L units cancel and mol units are introduced. It is a one-step conversion:
\[38.7\, \cancel{L}\times \frac{1\, mol}{22.4\cancel{L}}=1.73\, mol\nonumber \]
What volume does 4.87 mol of \(\ce{Kr}\) have at STP?
- Answer
-
109 L
What volume of \(\ce{H2}\) is produced at STP when 55.8 g of \(\ce{Zn}\) metal react with excess \(\ce{HCl}\)?
\[\ce{Zn(s) + 2HCl(aq) → ZnCl2(aq) + H2(g)} \nonumber \]
Solution
This is a stoichiometry problem with a twist: we need to use the molar volume of a gas at STP to determine the final answer. The first part of the calculation is the same as in a previous example:
\[55.8\cancel{g\, Zn}\times \frac{1\cancel{mol\, Zn}}{65.41\cancel{g\, Zn}}\times \frac{1\, mol\, H_{2}}{1\cancel{mol\, Zn}}=0.853\, H_{2}\nonumber \]
Now we can use the molar volume, 22.4 L/mol, because the gas is at STP:
\[0.853\cancel{mol\, H_{2}}\times \frac{22.4\, L}{1\cancel{mol\, H_{2}}}=19.1\, L\, H_{2}\nonumber \]
Alternatively, we could have applied the molar volume as a third conversion factor in the original stoichiometry calculation.
What volume of \(\ce{HCl}\) is generated if 3.44 g of \(\ce{Cl2}\) are reacted at STP?
\[\ce{H2(g) + Cl2(g) → 2HCl(g)} \nonumber \]
- Answer
-
2.17 L
The ideal gas law can also be used to determine the density of gases. Density, recall, is defined as the mass of a substance divided by its volume:
\[d=\dfrac{m}{V} \label{density}\]
Assume that you have exactly 1 mol of a gas. If you know the identity of the gas, you can determine the molar mass of the substance. Using the ideal gas law, you can also determine the volume of that mole of gas, using whatever the temperature and pressure conditions are. Then you can calculate the density of the gas by using
\[\text{density}=\dfrac{\text{molar mass}}{\text{molar volume}} \nonumber\]
What is the density of \(\ce{N2}\) at 25°C and 0.955 atm?
Solution
First, we must convert the temperature into kelvin:
\[25 + 273 = 298\, \ce{K} \nonumber\]
If we assume exactly 1 mol of \(\ce{N2}\), then we know its mass: 28.0 g. Using the ideal gas law, we can calculate the volume:
\[(0.955\, atm)V=(1\, mol)\left(0.08205\frac{L.atm}{mol.K}\right)(298\, K)\nonumber \]
All the units cancel except for \(L\), the unit of volume. So \(V = 25.6\,\ce{L}\)
Knowing the molar mass and the molar volume, we can determine the density of \(\ce{N2}\) under these conditions using Equation \ref{density}:
\[d=\frac{28.0\, g}{25.6\, L}=1.09\, g/L\nonumber \]
What is the density of \(\ce{CO2}\) at a pressure of 0.0079 atm and 227 K? (These are the approximate atmospheric conditions on Mars.)
- Answer
-
0.019 g/L
Breathing (more properly called respiration) is the process by which we draw air into our lungs so that our bodies can take up oxygen from the air. Let us apply the gas laws to breathing.
Start by considering pressure. We draw air into our lungs because the diaphragm, a muscle underneath the lungs, moves down to reduce pressure in the lungs, causing external air to rush in to fill the lower-pressure volume. We expel air by the diaphragm pushing against the lungs, increasing pressure inside the lungs and forcing the high-pressure air out. What are the pressure changes involved? A quarter of an atmosphere? A tenth of an atmosphere? Actually, under normal conditions, it's only 1 or 2 torr of pressure difference that makes us breathe in and out.
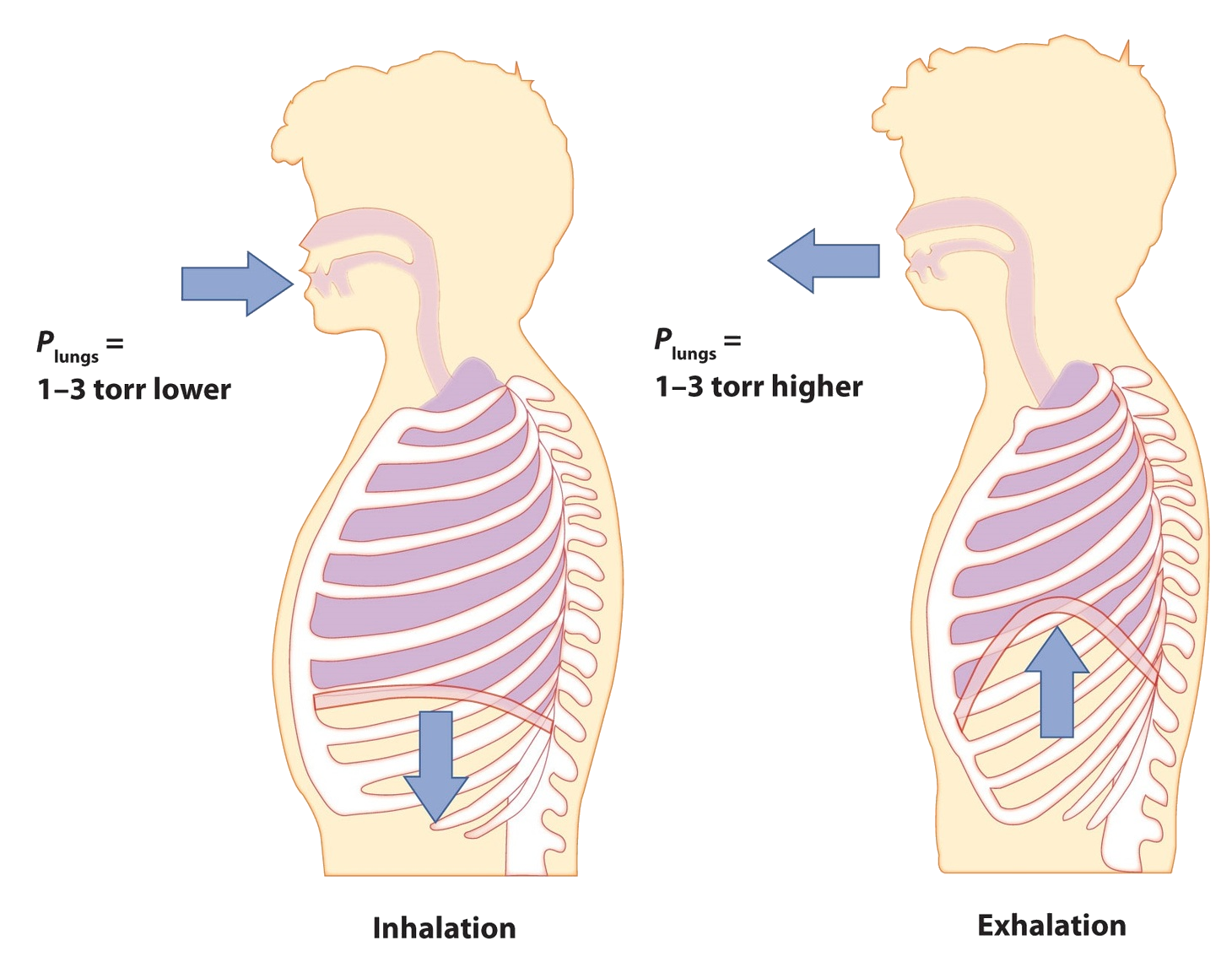
A normal breath is about 0.50 L. If room temperature is about 22°C, then the air has a temperature of about 295 K. With normal pressure being 1.0 atm, how many moles of air do we take in for every breath? The ideal gas law gives us an answer:
\[(1.0\, atm)(0.50\, L)=n \left(0.08205\dfrac{L.atm}{mol.K}\right)(295\, K)\nonumber \]
Solving for the number of moles, we get
\[n = 0.021\, \ce{mol\, air} \nonumber\]
This ends up being about 0.6 g of air per breath—not much, but enough to keep us alive.
Summary
- The ideal gas law relates the four independent physical properties of a gas at any time.
- The ideal gas law can be used in stoichiometry problems with chemical reactions that involve gases.
- Standard temperature and pressure (STP) are a useful set of benchmark conditions to compare other properties of gases.
- At STP, gases have a volume of 22.4 L per mole.
- The ideal gas law can be used to determine the density of gases.


