Ligand Field Theory Fundamentals
- Page ID
- 667
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ligand Field Theory can be considered an extension of Crystal Field Theory such that all levels of covalent interactions can be incorporated into the model. Treatment of the bonding in LFT is generally done using Molecular Orbital Theory. A qualitative approach that can be used for octahedral metal complexes is given in the following 3 diagrams.
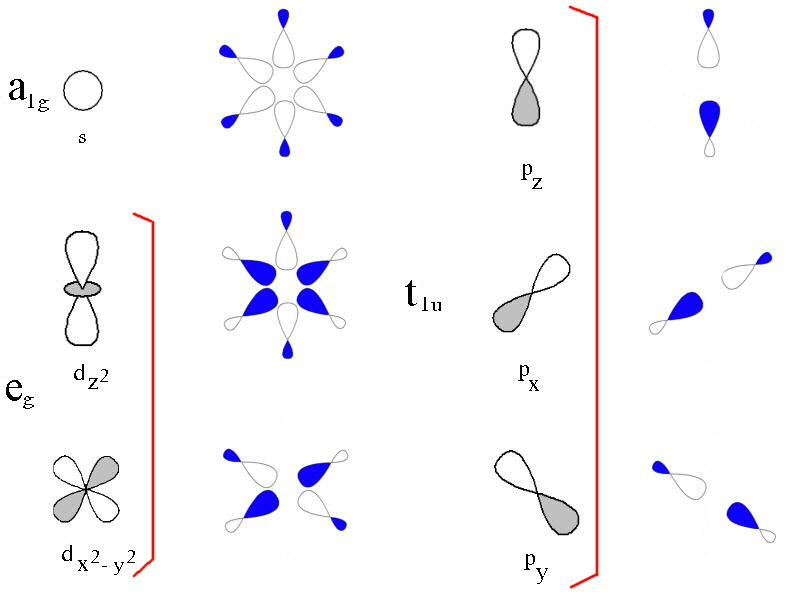
In the first diagram, the 3d, 4s and 4p metal ion atomic orbitals are shown together with the ligand group orbitals that would have the correct symmetry to be able to overlap with them. The symmetry adapted linear comination of ligand orbitals are generated by taking 6 sigma orbitals from the ligands, designated as σx, σ-x, σy, σ-y, σz, σ-z and then combining them to make 6 ligand group orbitals. (labelled eg, a1g, t1u)
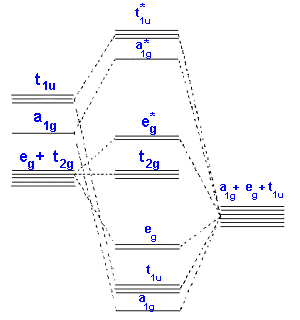
In the second diagram only sigma bonding is considered and it shows the combination of the metal 3d, 4s and 4p orbitals with OCCUPIED ligand group orbitals (using 1 orbital from each ligand). The result is that that the metal electrons would be fed into t2g and eg* molecular orbitals which is similar to the CFT model except that the eg orbital is now eg*.

For example: B - [M(II)I6]4- A - [M(II)(H2O)6]2+ C - [M(II)(CN)6]4-
In the third diagram, π (pi) bonding is considered. In general π bonds are weaker than σ (sigma) bonds and so the effect is to modify rather than dramatically alter the description. 2 orbitals from each ligand are combined to give a total of 12 which are subdivided into four sets with three ligand group orbitals in each set. These are labelled t1g, t1u, t2g and t2u. The metal t2g orbital is the most suitable for interaction and this is shown in the 2 cases above.
Case A is the same as above, ignoring π interactions.
- For case B, the ligand π orbitals are full and at lower energy than the metal t2g. This causes a decrease in the size of Δ.
- For case C, the ligand π orbitals are empty and at higher energy than the metal t2g. This causes an increase in the size of Δ.
Returning to the problem of correctly placing ligands in the Spectrochemical series, the halides are examples of case A and groups like CN- and CO are examples of case B. It is possible then to explain the Spectrochemical series once covalent effects are considered.
Some convincing arguments for covalency and effects on Δ come from a study of the IR spectra recorded for simple carbonyl compounds e.g. M(CO)6.
- The CO molecule has a strong triple bond which in the IR gives rise to a strong absorption at ~2140 cm-1. For the series [Mn(CO)6]+, [Cr(CO)6] and [V(CO)6]-, which are isoelectronic, the IR bands for the CO have shifted to 2090, 2000 and 1860 cm-1 respectively. Despite the fact that the metals have the same number of electrons (isoelectronic) the frequency of force constant of the CO bond is seen to vary Mn+ > Cr > V-.
- This can not be explained on an ionic basis but is consistent with the π bonding scheme since the greater the positive charge on the metal, the less readily the metal can delocalize electrons back into the π* orbitals of the CO group.
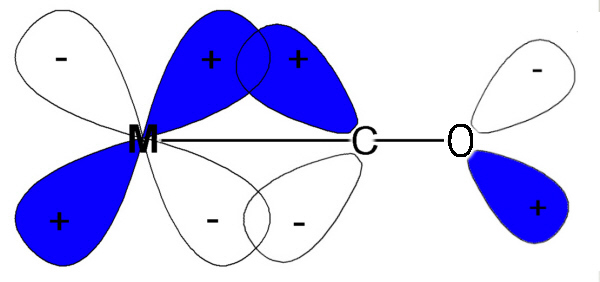
Note that the IR values we are dealing with relate to the CO bond and not the M-C so when the CO frequency gets less then it is losing triple bond character and becoming more like a double bond. This is expected if electrons are pushed back from the metal into what were empty π* antibonding orbitals.
Contributors and Attributions
Prof. Robert J. Lancashire (The Department of Chemistry, University of the West Indies)

