Acidity of the Hexaaqua Ions
- Page ID
- 3710
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page explains why complex ions of the type [M(H2O)6]n+ are acidic.
The Charge Distribution within Complex Ion
The pH's of solutions containing hexaaqua ions vary a lot from one metal to another (assuming you are comparing solutions of equal concentrations). However, the underlying explanation is the same for all of them. We'll take the hexaaquairon(III) ion, [Fe(H2O)6]3+ as typical. The structure of the ion is:
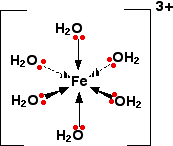
Each of the six water molecules are attached to the central iron(III) ion via a co-ordinate bond using one of the lone pairs on the oxygen. We'll choose one of these water molecules at random (it doesn't make any difference which one!), and look at the bonding in a bit more detail - showing all the bonds around the oxygen. Imagine for the moment that the 3+ charge is located entirely on the iron.
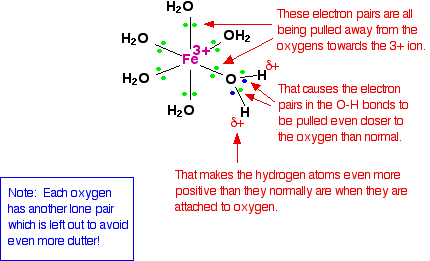
When the lone pairs on the oxygens form co-ordinate bonds with the iron, there is obviously a movement of electrons towards the iron. That has an effect on the electrons in the O-H bonds. These electrons, in turn, get pulled towards the oxygen even more than usual. That leaves the hydrogen nuclei more exposed than normal. The overall effect is that each of the hydrogen atoms is more positive than it is in ordinary water molecules. The 3+ charge is no longer located entirely on the iron but spread out over the whole ion - much of it on the hydrogen atoms.
The effect of dissolving this ion in water
The hydrogen atoms attached to the water ligands are sufficiently positive that they can be pulled off in a reaction involving water molecules in the solution. The first stage of this process is:
\[ \ce{ Fe(H2O)6^{3+} + H2O <=> Fe(H2O)5(OH)^{2+} + H3O^{+}} \label{eq1} \]
The complex ion is acting as an (Arrhenius) acid by donating a hydrogen ion to water molecules in the solution. The water is, of course, acting as a (Arrhenius) base by accepting the hydrogen ion. Because of the confusing presence of water from two different sources (the ligands and the solution), it is easier to simplify Equation \ref{eq1}:
\[ \ce{[Fe(H_2O)_6]^{3+} (aq) \rightleftharpoons [Fe(H2O)_5(OH)]^{2+} (aq) + H^{+} (aq)} \label{eq2} \]
However, if you write it like this, remember that the hydrogen ion is not just falling off the complex ion. It is being pulled off by a water molecule in the solution. Whenever you write "\(H^+(aq)\)" what you really mean is a hydroxonium ion, H3O+.
The hexaaquairon(III) ion is quite strongly acidic giving solutions with pH's around 1.5, depending on concentration. You can get further loss of hydrogen ions as well, from a second and a third water molecule since the complex ion is a polyprotic acid.
Losing a second hydrogen ion:
\[ \ce{ [Fe(H2O)5(OH)]^{2+} (aq) \rightleftharpoons [Fe(H_2O)_4(OH)_2]^{+} (aq) + H^+ (aq)} \label{eq3} \]
and a third one:
\[ \ce{ [ Fe(H_2O)_4(OH)_2]^{+} (aq) \rightleftharpoons [ Fe(H_2O)_3(OH)_3] (s) + H^+ (aq)} \label{eq4} \]
This time you end up with a neutral complex and because it has no charge, it does not dissolve to any extent in water, and a precipitate is formed.
In practice
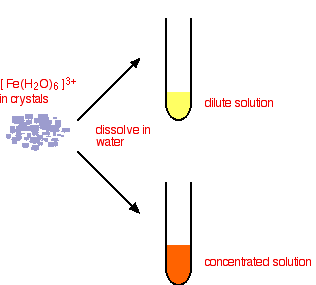
What do you actually get in solution if you dissolve an iron(III) salt in water? In fact you get a mixture of all the complexes that you have seen in the equations above. These reactions are all equilibria, so everything will be present. The proportions depend on how concentrated the solution is.
The color of the solution is very variable and depends in part on the concentration of the solution. Dilute solutions containing iron(III) ions can be pale yellow. More concentrated ones are much more orange, and may even produce some orange precipitate. None of these colors represents the true color of the [Fe(H2O)6]3+ ion - which is a very pale lilac color and is only really easy to see in solids containing the ion.
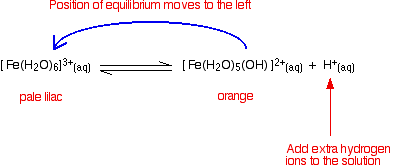
Looking at the equilibrium showing the loss of the first hydrogen ion:
\[ \underbrace{\ce{ Fe(H2O)6^{3+}}}_{\text{pale lilac}} + \ce{H2O} \ce{<=>} \underbrace{\ce{Fe(H2O)5(OH)^{2+}}}_{\text{orange}} + \ce{H3O^{+}} \nonumber \]
The color of the new complex ion on the right-hand side is so strong that it completely masks the color of the hexaaqua ion. In concentrated solutions, the equilibrium position will be even further to the right-hand side (Le Chatelier's Principle), and so the color darkens. You will also get significant loss of other hydrogen ions (Equation \ref{eq3} and \ref{eq4}) leading to some formation of the neutral complex and thus some precipitate.
The position of this equilibrium can be shifted by adding extra hydrogen ions from a concentrated acid (e.g., by adding concentrated nitric acid to a solution of iron(III) nitrate). The new hydrogen ions push the position of the equilibrium to the left so that you can see the color of the hexaaqua ion. This is slightly easier to follow if you write the simplified version of the equilibrium (Equation \ref{eq2}).
Solutions containing 3+ hexaaqua ions tend to have pH's in the range from 1 to 3. Solutions containing 2+ ions have higher pH's - typically around 5 - 6, although they can go down to about 3. Remember that the reason that these ions are acidic is because of the pull of the electrons towards the positive central ion. An ion with 3+ charges on it is going to pull the electrons more strongly than one with only 2+ charges.
In 3+ ions, the electrons in the O-H bonds will be pulled further away from the hydrogens than in 2+ ions. That means that the hydrogen atoms in the ligand water molecules will have a greater positive charge in a 3+ ion, and so will be more attracted to water molecules in the solution. If they are more attracted, they will be more readily lost - and so the 3+ ions are more acidic.
The Effect of ionic radius on acidity
If you have ions of the same charge, it seems reasonable that the smaller the volume this charge is packed into, the greater the distorting effect on the electrons in the O-H bonds. Ions with the same charge but in a smaller volume (a higher charge density) would be expected to be more acidic. You would therefore expect to find that the smaller the radius of the metal ion, the stronger the acid. Unfortunately, it's not that simple!
Unfortunately, almost every data source that you refer to quotes different values for ionic radii. This is because the radius of a metal ion varies depending on what negative ion it is associated with. We are interested in what happens when the metal ion is bonded to water molecules, so haven't got simple ions at all! Whatever values we take are unlikely to represent the real situation. In the graphs which follow I have taken values for ionic radii from two common sources so that you can see what a lot of difference it makes to the argument.
The graphs
If it is true that the smaller the ionic radius, the stronger the acidity of the hexaaqua ion, you would expect some sort of regular increase in pKa (showing weaker acids) as ionic radius increases. The following graphs plot pKa against ionic radii for the 2+ ions of the elements in the first transition series from vanadium to copper. The first graph plots pKa against ionic radii taken from Chemistry Data Book by Stark and Wallace.
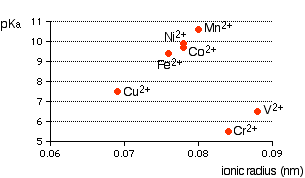
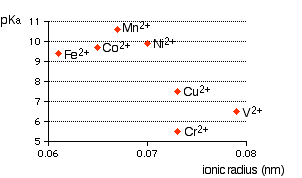
You can see that there is a trend for several of the ions, but it is completely broken by vanadium and chromium. The second graph uses ionic radii taken from the Nuffield Advanced Science Book of Data.
There probably is a relationship between ionic radius and acid strength, but that it is nothing like as simple and straightforward as most books at this level pretend. The problem is that there are other more important effects operating as well (quite apart from differences in charge) that can completely swamp the effect of the changes in ionic radius. You have to look in far more detail at the bonding in the hexaaqua ions and the product ions.
Contributors and Attributions
Jim Clark (Chemguide.co.uk)


