1.25: Electron Transfer Reactions
- Page ID
- 204727
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electron transfer reaction
Electron transfer reaction is a reaction in which a single electron is transferred from one molecule to another [1]. For example, a reaction that occurs when steel wool (made of iron atoms) is placed in a solution of CuSO4 is given in Figure \(\PageIndex{1}\) below:

This demonstration shows that the deep blue color of the CuSO4 solution (left picture), which is caused by the Cu2+ ions, becomes light green due to Fe2+ ions (right picture). As a result, a brown solid made of metallic copper forms and the steel wool disintegrates as the Fe atoms disappear. The reaction has thus led Fe to be converted to Fe2+ while the Cu2+ is converted to Cu. This indicates that the oxidation state of copper has changed from +2 in the Cu2+ ions in solution to 0 in the atoms comprising metallic copper. This is accomplished as each Fe atom gives up two electrons, while each Cu2+ gains two electrons, as a result of which two electrons are transferred from Fe atoms to Cu2+ ions in solution. This is an example of an electron transfer reaction. The reaction is given by: Cu2+ + Fe → Cu + Fe2+.
Mechanism of Electron Transfer Reactions
The process of electron transfer from one species to another species leads to the oxidation of the donor and reduction of the acceptor. The mechanism by which the electron transfer occurs between inorganic complexes can be classified in to two types: inner sphere electron transfer mechanism and outer sphere electron transfer mechanism.
Inner Sphere
Inner sphere electron transfer occurs between complexes via a bridging ligand. At least one of the complexes needs to be labile to allow the bridge to form. Bonds are broken and formed.
Outer Sphere
Outer sphere electron transfer occurs between two species that do not undergo substitution and do not involve the incursion of significant covalent bond formation. It occurs when none of the ligands can function as a bridge. It is faster than inner sphere because the energetic demands are less. No new bonds are broken or formed. Interaction between the two coordination spheres exist but is not as pronounced as for the bridge complex in the inner sphere. Outer Adduct is held together by one of the following: Electrostatic interactions, Vander Waals forces, or Hydrogen bonding.
Marcus Theory
In 1956, Rudolph A. Marcus developed the Marcus theory to explain the rates of electron transfer reactions. R.A. Marcus received the Nobel Prize in Chemistry in 1992 for this theory [3]. The rate of transfer refers movement of an electron from the electron donor to the electron acceptor. The theory was formulated to address outer sphere electron transfer reactions, in which the two chemical species (electron donor and acceptor) only change in their charge with an electron jumping but do not undergo large structural changes. Later, the theory included inner sphere electron transfer contributions, in which a change of distances or geometry in the solvation or coordination shells of the two chemical species is taken into account.
When electron transfer reactions involve no making or breaking of bonds, the Marcus theory limits the reaction partners to be weakly coupled and retain their individuality. The reorganization of the surroundings is thermally induced whereby the outer sphere (solvent) and the inner sphere (solvent sheath or ligands) create the geometrically favorable situation prior to and independent of the electron jump. The solvent is very important aspect of the theory and leads the way to the calculation of the Gibbs free energy of activation, using the polarization properties of the solvent, the size of the reactants, the transfer distance and the Gibbs free energy ΔG0 of the redox reaction. The most surprising result of Marcus' theory was the "inverted region": whereas the reaction rates usually become higher with increasing exergonicity of the reaction, electron transfer should, according to Marcus theory, become slower in the very negative ΔG0 domain.
If a redox reaction is assumed, one partner acts as an electron donor D the other as an acceptor A. As these are neutral molecules electrostatic forces may be ignored. In addition, either D or A may be considered to be in a photoexcited state (photoinduced electron transfer, PET). Other than a change in the starting stage energies, the principles of Marcus’ model apply equally well to both ground and excited state electron transfer. For a reaction to take place D and A must diffuse together. They form the precursor complex, usually a kinetic, unstable, solvated encounter complex, which by electron transfer is transformed to the successor complex, and finally this separates by diffusion. For a one electron transfer the reaction is:
k12 k23 k30 D+A<=> [D…A] <=> [D+…A-] D+ + A- k21 k32
Where, k12, k21 and k30 are diffusion constants, k23 and k32 rate constants of activated reactions.
Since redox reactions are preferably run in polar solvents, D and A have a solvent shell and the precursor and successor complexes are solvated also. The closest molecules of the solvent shell, or the ligands in complexes, are tightly bound and constitute the "inner sphere". Reactions in which these participate are called inner sphere redox reactions. The free solvent molecules constitute the "outer sphere". Outer sphere redox reactions do not change the inner sphere, no bonds are made nor broken. Only an electron transfer takes place.
A quite simple example is the Fe2+/Fe3+ redox reaction, the self exchange reaction which is known to be always occurring in an aqueous solution containing both FeSO4 and Fe2(SO4)3 (of course, with equal and measurable rates in both directions and with Gibbs free reaction energy ΔG0 = 0). For outer sphere redox reactions there cannot be such a reaction path, but nevertheless one does observe an activation energy.
Since the electron as an elementary particle cannot be divided, it resides either on the donor or the acceptor and arranges the solvent molecules accordingly in an equilibrium. The "transition state", on the other hand, requires a solvent configuration which would result from the transfer of half an electron, which is impossible. This means that real charge distribution and required solvent polarization are not in an "equilibrium". Yet it is possible that the solvent takes a configuration corresponding to the "transition state", even if the electron sits on the donor or acceptor. This, however, requires energy. This energy may be provided by the thermal energy of the solvent and thermal fluctuations can produce the correct polarization state.
Marcus developed a classical theory with the aim of calculating the polarization energy of the said non-equilibrium state. From thermodynamics it is well known that the energy of such a state can be determined if a reversible path to that state is found. Marcus was successful in finding such a path via two reversible charging steps for the preparation of the "transition state" from the precursor complex. Marcus states that four elements are essential for the model on which the theory is based: 1. A classical, purely electrostatic model must be employed. The charge may be transferred in any portion from one body to another. 2. The fast electron polarization Pe and the slow atom and orientation polarization Pu of the solvent are to be separated on grounds of their time constants differing several orders of magnitude. 3. He further separates the inner sphere (reactant + tightly bound solvent molecules, in complexes + ligands) and the outer sphere (free solvent) 4. In this model Marcus confines himself to calculating the outer sphere energy of the non-equilibrium polarization of the "transition state". The outer sphere energy is often much larger than the inner sphere contribution because of the far reaching electrostatic forces.
In this classical model the transfer of any arbitrary amount of charge Δe is possible. So, the energy of the non-equilibrium state, and consequently of the polarization energy of the solvent, can be probed as a function of Δe. Thus, Marcus has lumped together the coordinates of all solvent molecules into a single coordinate of solvent polarization Δp, which is determined by the amount of transferred charge Δe. So, he reached a simplification of the energy representation to only two dimensions: G = f(Δe). The result for two conducting spheres in a solvent is the formula of Marcus
Where r1 and r2 are the radii of the spheres and R is their separation, εs and εopt are the static and high frequency (optical) dielectric constants of the solvent, Δe the amount of charge transferred. The graph of G vs. Δe is a parabola (Figure \(\PageIndex{2}\)). In Marcus theory the energy belonging to the transfer of a unit charge (Δe = 1) is called the (outer sphere) reorganization energy λo, i.e. the energy of a state where the polarization would correspond to the transfer of a unit amount of charge, but the real charge distribution is that before the transfer. In terms of exchange direction the system is symmetric.
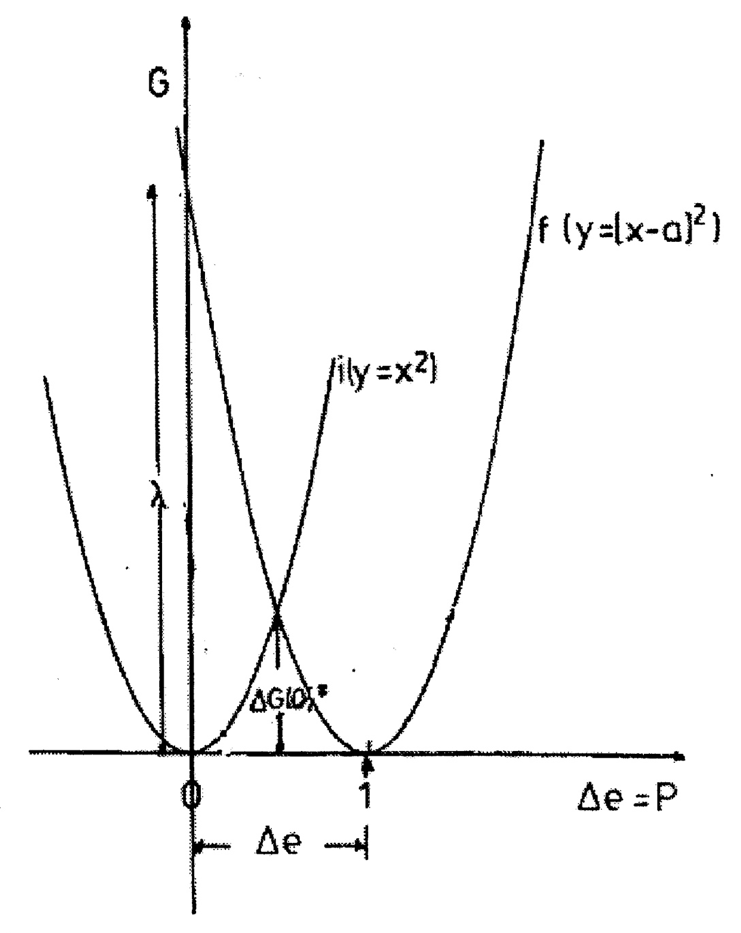
Marcus theory is used to describe a number of important processes in chemistry and biology, including photosynthesis, corrosion, certain types of chemiluminescence, charge separation in some types of solar cells and more. Besides the inner and outer sphere applications, Marcus theory has been extended to address heterogeneous electron transfer.
References
1. Dennis Wertz, Chemistry - A Molecular Science (eBook). 3rd edition.
2. Dennis Wertz. Web. http://www.webassign.net/question_assets/wertzcams3/ch_11/manual.html
3. Rudolph Marcus (1956). On the Theory of Oxidation‐Reduction Reactions Involving Electron Transfer. I. The Journal of Chemical Physics 24(5):966-978


