1.2: Molecular Point Groups
- Page ID
- 183432
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
A Point Group describes all the symmetry operations that can be performed on a molecule that result in a conformation indistinguishable from the original. Point groups are used in Group Theory, the mathematical analysis of groups, to determine properties such as a molecule's molecular orbitals.
Assigning Point Groups
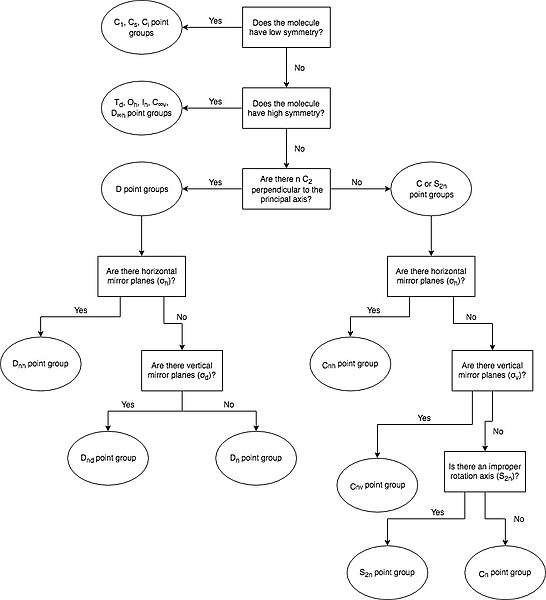
While a point group contains all of the symmetry operations that can be performed on a given molecule, it is not necessary to identify all of these operations to determine the molecule's overall point group. Instead, a molecule's point group can be determined by following a set of steps which analyze the presence (or absence) of particular symmetry elements.
- Determine if the molecule is of high or low symmetry.
- If not, find the highest order rotation axis, Cn.
- Determine if the molecule has any C2 axes perpendicular to the principal Cn axis. If so, then there are n such C2 axes, and the molecule is in the D set of point groups. If not, it is in either the C or S set of point groups.
- Determine if the molecule has a horizontal mirror plane (σh) perpendicular to the principal Cn axis. If so, the molecule is either in the Cnh or Dnh set of point groups.
- Determine if the molecule has a vertical mirror plane (σv) containing the principal Cn axis. If so, the molecule is either in the Cnv or Dnd set of point groups. If not, and if the molecule has n perpendicular C2 axes, then it is part of the Dn set of point groups.
- Determine if there is an improper rotation axis, S2n, collinear with the principal Cn axis. If so, the molecule is in the S2n point group. If not, the molecule is in the Cn point group.
Find the point group of benzene (C6H6).
- Solution
-
- Highest order rotation axis: C6
- Benzene is neither high or low symmetry
- There are 6 C2 axes perpendicular to the principal axis
- There is a horizontal mirror plane (σh)
Benzene is in the D6h point group.
Low Symmetry Point Groups
Low symmetry point groups include the C1, Cs, and Ci groups
| Group | Description | Example |
|---|---|---|
| C1 | only the identity operation (E) | CHFClBr |
| Cs | only the identity operation (E) and one mirror plane | C2H2ClBr |
| Ci | only the identity operation (E) and a center of inversion (i) | C2H2Cl2Br |
High Symmetry Point Groups
High symmetry point groups include the Td, Oh, Ih, C∞v, and D∞h groups. The table below describes their characteristic symmetry operations. The full set of symmetry operations included in the point group is described in the corresponding character table.
| Group | Description | Example |
|---|---|---|
| C∞v | linear molecule with an infinite number of rotation axes and vertical mirror planes (σv) | HBr |
| D∞h | linear molecule with an infinite number of rotation axes, vertical mirror planes (σv), perpendicular C2 axes, a horizontal mirror plane (σh), and an inversion center (i) | CO2 |
| Td | typically have tetrahedral geometry, with 4 C4 axes, 3 C2 axes, 3 S4 axes, and 6 dihedral mirror planes (σd) | CH4 |
| Oh | typically have octahedral geometry, with 3 C4 axes, 4 C3 axes, and an inversion center (i) as characteristic symmetry operations | SF6 |
| Ih | typically have an icosahedral structure, with 6 C5 axes as characteristic symmetry operations | B12H122- |
D Groups
The D set of point groups is classified as Dnh, Dnd, or Dn, where n refers to the principal axis of rotation. Overall, the D groups are characterized by the presence of n C2 axes perpendicular to the principal Cn axis. Further classification of a molecule in the D groups depends on the presence of horizontal or vertical/dihedral mirror planes.
| Group | Description | Example |
|---|---|---|
| Dnh | n perpendicular C2 axes, and a horizontal mirror plane (σh) | benzene, C6H6 is D6h |
| Dnd | n perpendicular C2 axes, and a vertical mirror plane (σv) | propadiene, C3H4 is D2d |
| Dn | n perpendicular C2 axes, no mirror planes | [Co(en)3]3+ is D3 |
C Groups
The C set of point groups is classified as Cnh, Cnv, or Cn, where n refers to the principal axis of rotation. The C set of groups is characterized by the absence of n C2 axes perpendicular to the principal Cn axis. Further classification of a molecule in the C groups depends on the presence of horizontal or vertical/dihedral mirror planes.
| Group | Description | Example |
|---|---|---|
| Cnh | horizontal mirror plane (σh) perpendicular to the principal Cn axis | boric acid, H3BO3, is C3h |
| Cnv | vertical mirror plane (σv) containing the principal Cn axis | ammonia, NH3, is C3v |
| Cn | no mirror planes | P(C6H5)3 is C3 |
S Groups
The S set of point groups is classified as S2n, where n refers to the principal axis of rotation. The S set of groups is characterized by the absence of n C2 axes perpendicular to the principal Cn axis, as well as the absence of horizontal and vertical/dihedral mirror planes. However, there is an improper rotation (or a rotation-reflection) axis collinear with the principal Cn axis.
| Group | Description | Example |
|---|---|---|
| S2n | improper rotation (or a rotation-reflection) axis collinear with the principal Cn axis | 12-crown-4 is S4 |


