8.1.2: Electronegativity increases and radius decreases towards the upper left of the periodic table, with electron withdrawing substituents, and with oxidation state

The physical and chemical properties of main group compounds depend in part on the electronegativity of the atoms involved.

Electronegativity is somewhat loosely defined as the ability of atoms to attract electrons towards themselves in covalent bonds. When atoms that differ in electronegativity form a covalent bond, the bonding electrons are not shared equally. Instead, the bonding electrons are more strongly attracted towards the more electronegative atom, resulting in a polar bond, as shown in Scheme \(\PageIndex{I}\).

Scheme \(\PageIndex{I}\). (a) The bonding electrons in molecular diiodine's homopolar bond are shared equally (b), while those in iodine monofluoride are more strongly attracted to the fluorine nucleus, polarizing the bond towards the fluorine.

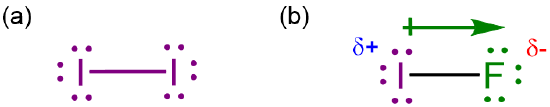
Because electronegativity determines the polarity of bonds and by extension molecules, it is one of the key determinants of the chemical and physical properties of main group compounds.

A classic example of the influence of bond polarity on reactivity involves the group IV/14 element hydrides. Carbon hydrides like methane and other alkanes do not react with water, alcohols, and other Brønsted acids, while silanes, germanes, and stannanes do. For example

\[ \sf{CH_4 + 4HOEt \rightarrow No~~reaction} \nonumber \]

\[ \sf{SiH_4 + 4HOEt \rightarrow Si(OEt)_4 + 4 H_2 } \nonumber \]

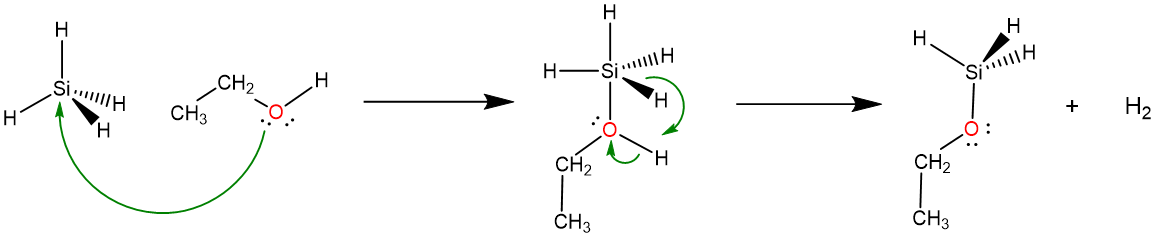
This difference in reactivity reflects two factors. The first is a kinetic one. The ability of the larger Si atom to more readily add an additional ligand to give a relatively stable trigonal bipyramidal intermediate provides a relatively low energy pathway for the reaction, enabling it to take place quickly.

\[ \nonumber \]

The second and much more important factor that determines the difference in reactivity is thermodynamic and has to do with the polarities of the C-H and Si-H bonds. These polarities depend on the electronegativities of carbon, silicon, hydrogen, and oxygen as depicted in Scheme \(\PageIndex{I}\). As can be seen in part a of Scheme \(\PageIndex{I}\), because carbon's electronegativity is greater than that of H, the hydrogens of C-H bonds are electrophilic and act as weak Brønsted acids, rendering them unreactive towards other Brønsted acids like alcohols. In contrast, as shown in part b, silicon's electronegativity is lower than that of H, so that the polarization of Si-H bonds facilitates both elimination of the Si-H and O-H as \(\sf{H_2}\) and nucleophilic attack of the ethanol O at the Si center.

Scheme \(\PageIndex{II}\). Structures of silane, methane, and ethanol showing the electronegativites of C, Si, H, and O in green. (a) In the case of methane the C-H bonds are polarized to disfavor nucleophilic addition of the ethanol oxygen and elimination of the C-H and O-H hydrogens. (b) In contrast, the polarity of silane's Si-H bonds facilitates both nucleophilic addition and elimination of the Si-H and O-H hydrogens as \(\sf{H_2}\).

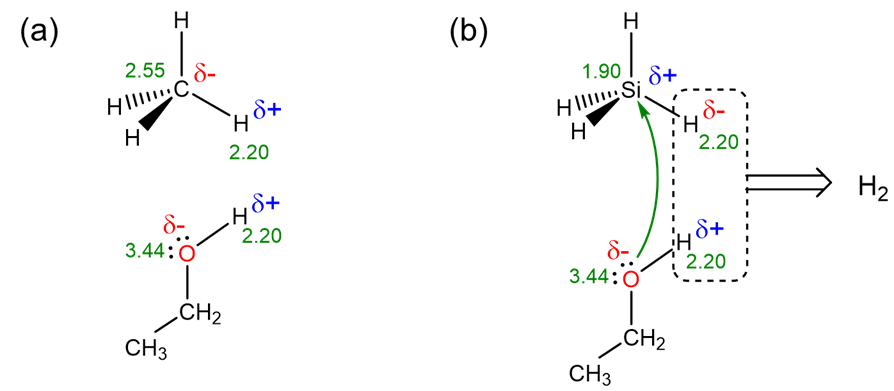
The Pauling scale is the most commonly used scale to rate electronegativities.

Electronegativity is most commonly quantified using the Pauling scale. The Pauling scale is based on the observation that polar bonds are generally stronger than the average of their homopolar counterparts. This is well illustrated by the bond energies of H₂, Cl₂, and HCl given in Table \(\PageIndex{1}\). As may be seen from the table, the average of the H-H and F-F bond energy of 295.5 kJ/mol is only 52% of the H-F bond energy of 567 kJ/mol.

Table \(\PageIndex{1}\). Bond energies of H₂, Cl₂, and HCl.

Figure \(\PageIndex{2}\).

Figure \(\PageIndex{1}\). Electrostatic attraction between partial atomic charges in HF.

In this model the greater the bond polarity (larger \( \delta^+\) and \( \delta^-\) ), the larger the "excess bond strength." Consequently the "excess bond strength"may be used as an empirical measure of the difference between the electronegativities \(\chi\) of the elements involved.  Pauling did this using equation \(\PageIndex{2}\):

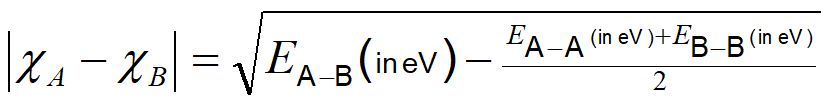\[ \nonumber \]

where A and B are a given pair of elements.

Equation \(\PageIndex{2}\) may only be used to determine differences in electronegativities. To determine absolute electronegativities, Pauling assigned the electronegativity of the most electronegative element in his scale, F, a value of 4.00, although to accomodate more accurate thermochemical data the Pauling electronegativity of F has since been adjusted to 3.98. Pauling electronegativities are given for the elements in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{3}\). Pauling electronegativities of the elements. Taken from https://chem.libretexts.org/Courses/Mount_Royal_University/Chem_1201/Unit_2._Periodic_Properties_of_the_Elements/2.12%3A_Electronegativity

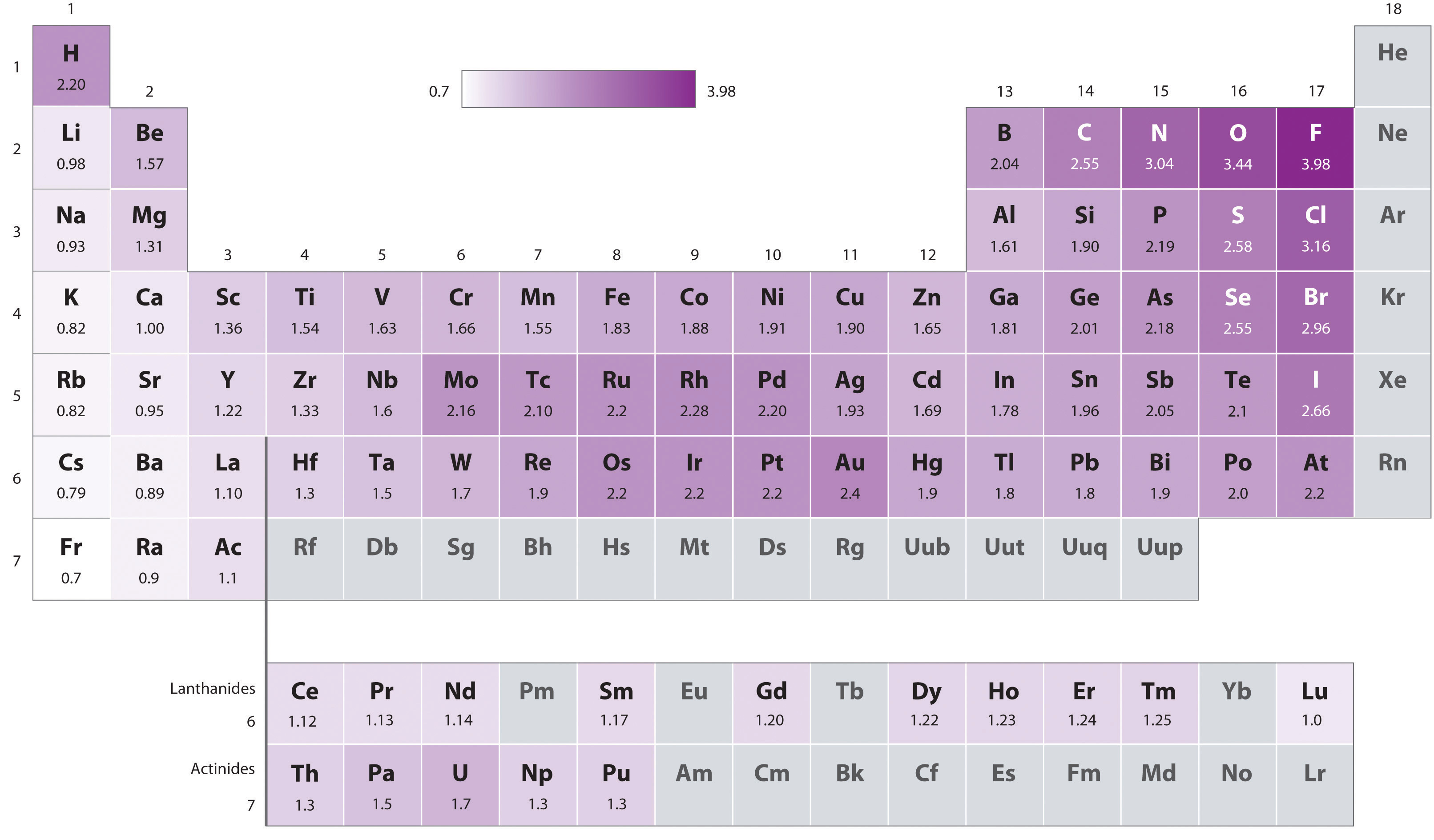
Electronegativity generally increases across a row and decreases down a group

As can be seen from the Pauling electronegativity values in Figure \(\PageIndex{4}\), within the main group electronegativity decreases down a group and roughly increases on moving from left to right across a group - i.e., electronegativity roughly increases on moving from the lower left to the upper right of the periodic table.

Figure \(\PageIndex{4}\). Pauling electronegativities of the main group elements. Adapted from https://chem.libretexts.org/Courses/Mount_Royal_University/Chem_1201/Unit_2._Periodic_Properties_of_the_Elements/2.12%3A_Electronegativity

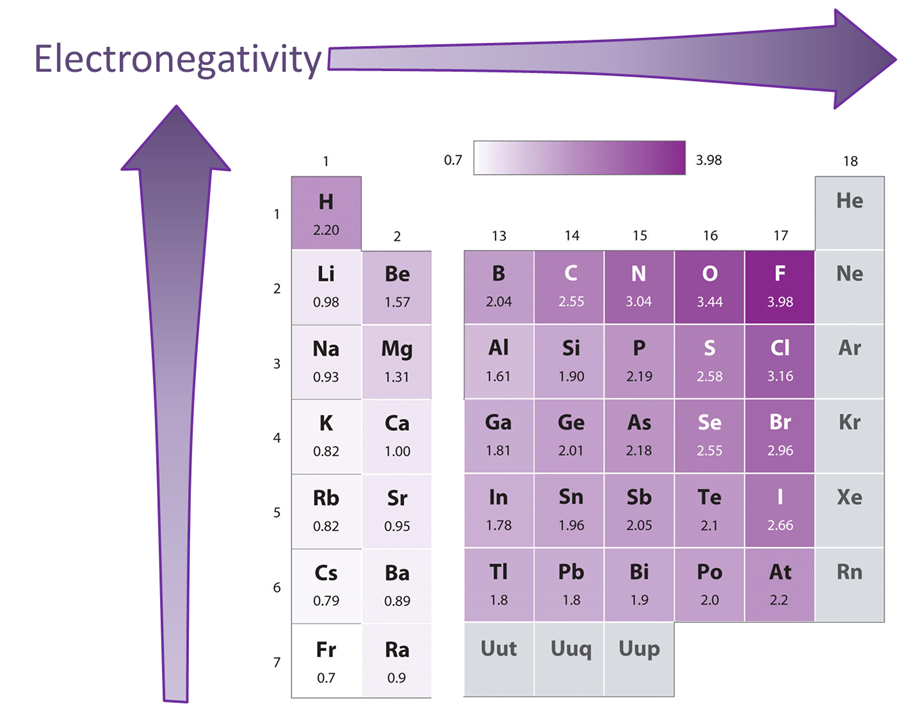
Two factors modify the overall pattern of increasing electronegativity on moving to the upper right of the periodic table.

The first is the aforementioned ambiguous position of hydrogen. The electronegativity of hydrogen does agree with this overall pattern if hydrogen is placed at the head of the alkali metal group. However, it is over a full unit higher than any other alkali metal and, if placed at the head of the halogen group, would be almost two units lower than that of F.

The second is the reversal of the expected decrease in electronegativity down a group for the pairs Al & Ga and Si & Ge. This is because the post transition metals have anomalously high electronegativities due to the increasing effective nuclear charge associated with the filling of the d block - i.e., a sort of d-block contraction for electronegativity. The net effect is that the post transition elements in the p block all have anomalously high electronegativities. In the cases of Al & Ga and Si & Ge this results in an increase in electronegativity down the group as one moves from row 3 to row 4. In the case of the other post-transition elements it is seen that the movement between these two rows involves a modest decrease in electronegativity.

The electronegativity trends lead to diagonal relationships in which elements just to the left of and down a column to one another have similar chemical properties.

The increase in electronegativity across a row of the periodic table is sometimes compensated for by the decrease in electronegativity down a group, so that elements so diagonally related sometimes have similar electronegativities. Some such diagonally related elements have similar physical and chemical properties, although these similarities may not be due to the effect of electronegativity alone. Since atomic size also decreases across a row and increases down a group, some similarities reflect size effects as well. In any event, the result is that there are recognized diagonal relationships of chemical and physical similarity among elements diagonal to one another in the periodic table. Some of the more prominent diagonal relationships within the main group are shown in Figure \(\PageIndex{5}\).

Figure \(\PageIndex{5}\). Some commonly recognized diagonal relationships among the main group elements, which are listed along with their Pauling electronegativities and calculated Van der Waals radii. The radii are taken as the radii calculated at the CCSD(T) level using an ANO-RCC basis set as reported in Mantina, M.; Chamberlin, A. C.; Valero, R.; Cramer, C. J.; Truhlar, D. G., Consistent van der Waals Radii for the Whole Main Group. The Journal of Physical Chemistry A 2009, 113 (19), 5806-5812. The image is adapted from https://chem.libretexts.org/Courses/Mount_Royal_University/Chem_1201/Unit_2._Periodic_Properties_of_the_Elements/2.12%3A_Electronegativity

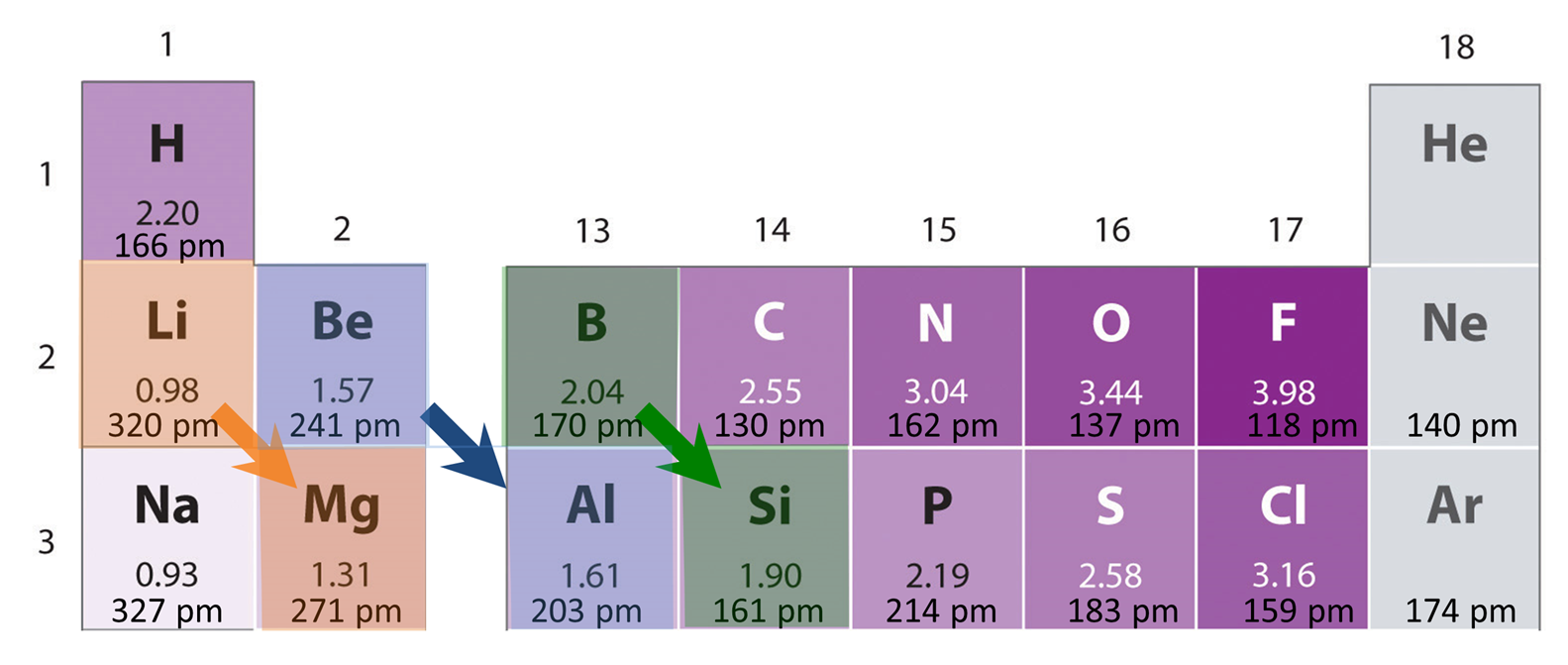
A few observations illustrate how these diagonal relationships work.

• Li & Mg – Lithium acts like Mg in that it is the only alkali metal to form stable nitride (Li₃N), oxide (Li₂O), and THF soluble alkyl carbanion salts as alkaline Earth metals do. This may be seen in the similar compounds formed by Li and Mg shown in Table \(\PageIndex{2}\). In contrast, the larger alkali metals form insoluble polymeric carbanion reagents, superoxides or peroxides and not oxides, and extremely unstable nitrides.

Table \(\PageIndex{2}\). Similar compounds formed by the diagonally related elements Li and Mg.

Type of compound	Li	Mg
oxide	\(\sf{Li_2O}\)	\(\sf{MgO}\)
nitride	\(\sf{Li_3N}\)	\(\sf{Mg_3N_2}\)
alkyl carbanion reagent	alkyllithium (RLi)	Gringard Reagent (RMg^+)

• Be & Al – In contrast to the basic oxides and hydroxides of most alkali metals and the heavier group 13 elements, both Be and Al form amphoteric oxides and hydroxides (\(Table \PageIndex{3}\)). Like Be and the remaining alkali metals, aluminum also forms a carbide (C^4-“salt”) instead of an acetylide (C₂^2-) or allylide (C₃^4-).

Table \(\PageIndex{3}\). Amphoteric behavior of the oxides and hydroxides of beryllium and aluminum.

Reaction	Be	Al
Oxide hydrolysis to hydroxide	\[\sf{BeO + H_2O \rightarrow Be(OH)_2} \nonumber \]	\[\sf{Al_2O_3 + 3H_2O \rightarrow 2 Al(OH)_3} \nonumber \]
Hydroxide as an Arrhenius and Brønsted Base	\[\sf{Be(OH)_2 \rightarrow BeO(OH)^+ + OH^-} \nonumber \] or \[\sf{Be(OH)_2 + 2H^+ \rightarrow Be^{2+} + 2H_2O} \nonumber \]	\[\sf{Al(OH)_3 \rightarrow 2 AlO(OH)_2^+ + OH^-} \nonumber \] or \[\sf{Al(OH)_3 + 3H^+ \rightarrow Al^{3+} + 3H_2O} \nonumber \]
Hydroxide as a Lewis Acid	\[\sf{Be(OH)_2 + 2OH^- \rightarrow Be(OH)_4^{2- }} \nonumber \]	\[\sf{Al(OH)_3 + OH^- \rightarrow 2 AlO(OH)_4^-} \nonumber \]

• B & Si - Both of these elements act as semiconductors, form acidic complex polymeric covalent oxides containing interlinked EO₄ tetrahedra, and their halides (BCl₃ & SiCl₄) act as acid halides. In contrast, the oxides of carbon (CO and CO₂) are monomeric, while the oxides of the heavier cogeners of these elements (Al₂O₃, Ga₂O₃, In₂O₃, In₂O, Tl₂O and GeO₂, SnO₂, PbO₂, and PbO) are considered ionic oxides. The halides of the heavier cogeners of Si more readily act as ionic oxides, while the binary halides of carbon (e.g., compounds like CCl₄) are usually not readily hydrolyzed.

The Mulliken and Allred-Rochow Electronegativity Scales connect Electronegativity to other Atomic Properties

While the Pauling scale considers electronegativity in terms of bonding, there are a number of other electronegativity scales that define electronegativity as a function of other atomic properties. Two of these will be considered here: the Mulliken (or Mulliken-Jaffe) scale, which defines electronegativity in terms of electron affinity and ionization energy (and by extension orbital energies), and the Allred-Rochow scale, which considers electronegativity in terms of effective nuclear charges.

The Mulliken Electronegativity Scale defines electronegativity in terms of Electron Affinity and Ionization Energy

The Mulliken definition of electronegativity was previously described in connection with absolute hardness and softness as the first derivative of a species energy with respect to changes in total number of electrons, \(N_{e^-}\).

\[Mulliken~electronegativity = χ = \dfrac{d E}{dN_{e^-}} \nonumber \]

\(\sf{where~~E~~is~~in~~eV}\)

Since this derivative is difficult to evaluate experimentally, the Mulliken electronegativity is typically approximated as the average of the species' ionization energy and electronegativity.

\[Mulliken~~electronegativity = χ ≈ \dfrac{IE + EA}{2} \nonumber \]

\(\sf{where~~IE~~and~~EA~~are~~in~~eV}\)

which, if the IE is approximated by Koopman's theorem as the opposite of the energy of the lowest unoccupied atomic orbital (LUAO) \(\sf{(IE = -E_{HOMO})}\) and the EA as the opposite of the energy released on absorption of an electron, may be taken as an approximation of the LUMO energy.

\[E_{LUMO} ≈ -EA \nonumber \]

and the Mulliken electronegativity is just the average of the HOAO and LUAO energies (~Fermi energy):

\[Mulliken~electronegativity, χ ≈ -\dfrac{E_{LUAO} + E_{HOAO}}{2} \nonumber \]

\(\sf{where~~all~~values~~are~~for~~the~~gas~~phase~~atoms~~in~~units~~of~~eV}\)

The Allred-Rochow Electronegativity Scale defines electronegativity in terms of the effective nuclear charge experienced by the valence electrons.

The Allred-Rochow electronegativity scale attempts to quantify electronegativity in terms of the electrostatic force attracting the bonding electrons to the atomic center. It does this by calculating the electronegativity as the associated electrostatic force.

\[ \sf{\chi_{Allred-Rochow,~raw} = - \dfrac{1}{4\pi \epsilon_0} \dfrac{e^2Z*}{r_{bond}^2}} \nonumber \]

These raw values have units of force (N/electron or dyne/electron) and do not correspond closely to electronegativity values reported on the Pauling Scale. Consequently, an empirical correction factor is used to adjust the scale to give electronegativities that more closely correspond to their Pauling equivalents.

\[ \sf{\chi_{Allred-Rochow} = 3590\dfrac{e^2Z*}{r_{bond}^2}} \nonumber \]+0.744

Mulliken electronegativities so calculated are given in Table \(\PageIndex{4}\).

Table \(\PageIndex{4}\): Allred-Rochow Electronegativity Values. Copied from https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Physical_Properties_of_Matter/Atomic_and_Molecular_Properties/Electronegativity/Allred-Rochow_Electronegativity

H 2.20

Li 0.97

Be 1.47

B 2.01

C 2.50

N 3.07

O 3.50

F 4.10

Na 1.01

Mg 1.23

Al 1.47

Si 1.74

P 2.06

S 2.44

Cl 2.83

K 0.91

Ca 1.04

Sc 1.20

Ti 1.32

V 1.45

Cr 1.56

Mn 1.60

Fe 1.64

Co 1.70

Ni 1.75

Cu 1.75

Zn 1.66

Ga 1.82

Ge 2.02

As 2.20

Se 2.48

Br 2.74

Rb 0.89

Sr 0.99

Y 1.11

Zr 1.22

Nb 1.23

Mo 1.30

Te 1.36

Ru 1.42

Rh 1.45

Pd 1.35

Ag 1.42

Cd 1.46

In 1.49

Sn 1.72

Sb 1.82

Te 2.01

I 2.21

Cs 0.86

Ba 0.97

La 1.08

Hf 1.23

Ta 1.33

W 1.40

Re 1.46

Os 1.52

Ir 1.55

Pt 1.44

Au 1.42

Hg 1.44

Tl 1.44

Pb 1.55

Bi 1.67

Po 1.76

At 1.90

These values correlate reasonably well with Pauling electronegativities. One consequence of this good agreement is that both scales are useful for making qualitative predictions about a substance's chemical behavior. For this reason most chemists continue to use the Pauling scale. In this respect, perhaps the greatest value of the Mulliken and Allred-Rochow electronegativity scales for the bench chemist lies in how they connect electronegativity to parameters that may be used to tailor molecular structure and reactivity, namely, substituent effects and oxidation states.

The effective electronegativity of an atom varies increases with oxidation state and in the presence of electron withdrawing substituents

One of the advantages of the Allred-Rochow and Mulliken electronegativity systems over that of Pauling's is that they can consider electronegativity in the context of compounds, in which electron donating and withdrawing groups modify the ability of atomic centers to attract electrons in a bond. As was considered in the section on measures of hardness, the Mulliken scale can be used to define the electronegativity of Lewis acid centers simply by considering the HOMO and LUMO energy in place of the HOAO and LUAO energies.

\[Mulliken~electronegativity~of~Lewis~acid, χ ≈ -\dfrac{E_{LUAO} + E_{HOAO}}{2} \nonumber \]

\(\sf{where~~all~~values~~are~~in~~units~~of~~eV}\)

The Allred-Rochow scale is not usually applied directly to molecules. However, its model of electronegativity as a measure of the electrostatic force experienced by the valence electrons may be applied to atoms in molecules, specifically by accounting for the influence of electron donating and withdrawing substituents on the effective nuclear charge an electron experiences. This is not usually done in any sort of rigorous way, and in the context of a typical advanced inorganic chemistry course, the influence of substituent groups on an atom's electronegativity may be estimated in one of two ways:

1. The group electronegativity concept may be used to quantitatively estimate an atom or functional group's electronegativity. A group electronegativity is the electronegativity of an atom that has been modified by attaching it to one or more substituents. These substituents modify the atom's base electronegativity by an amount equal to their empirically-determined substituent constants so that the group electronegativity, \( \chi_\sf{group}\), may be calculated.¹

\[ \chi_\sf{group} = \chi_\sf{base} + \sigma_\sf{substituent} \nonumber \]

where \( \chi_\sf{base}\) and \(\sigma_\sf{substituent}\) are the group's base electronegativity and the substituent constant, respectively. Because the substituent constant must be known in order to calculate group electronegativities, the group electronegativity concept has primarily been applied to organic compounds.

2. The effect of substituents on electronegativity may be qualitatively rationalized in terms of inductive effects and oxidation state. In this system

• electron donating groups decrease Z* and consequently a center's effective electronegativity; conversely, by increasing the Z* experienced by an atom's valence electrons, electron withdrawing groups increase its effective electronegativity.
• when an atomic center is oxidized, Z* and its effective electronegativity increase, while when it is reduced, Z* and its effective electronegativity decrease. This effect is commonly manifested as an increase in the acidity of polarized E-OH units as the oxidation state of the central element (E) increases, as illustrated for the inorganic oxyacids in Table \(\PageIndex{4}\).

Table \(\PageIndex{4}\). \(pK_a\) vales for selected oxyacids illustrating the increase in Brønsted acidity with central atom oxidation state.²

Acid	Central atom oxidation state	\(pK_a\) (\(pK_{a1}\) unless otherwise noted)
H2SO3	S^IV	1.9
H2SO4	S^VI	<0
HNO2	N^III	3.1
HNO3	N^V	<0
H3PO3	P^III	3.1
H3PO4	P^V	1.3
HClO	Cl^I	7.40
HClO2	Cl^III	1.94
HClO3	Cl^V	-2.7 (predicted)
HClO4	Cl^VII	~ -15^3

References

1. Davis, M. A., Group electronegativity and polar substituent constants. The Journal of Organic Chemistry 1967, 32 (4), 1161-1163.

2. All \(pK_a\) values with the exception of that of HClO₄ and HClO₃ are taken from Perrin, D. D., Ionization Constants of Inorganic Acids and Bases in Aqueous Solution, Second Edition, Pergamon, Oxford, 1982.

3. The \(pK_a\) value of HClO₄ is taken from Trummal, A.; Lipping, L.; Kaljurand, I.; Koppel, I. A.; Leito, I., Acidity of Strong Acids in Water and Dimethyl Sulfoxide. The Journal of Physical Chemistry A 2016, 120 (20), 3663-3669.

Contributors and Attributions

Stephen M. Contakes, Westmont College

All line drawings on this page are by Stephen Contakes and licensed under a Creative Commons Attribution 4.0 International License.

To the extent it is possible to do so, all modified figures on this page made by Stephen Contakes are licensed under a Creative Commons Attribution 4.0 International License.